A small mass m starts from rest and slides down the surface of a frictionless solid sphere of radius R. Calculate the angle at which the mass flies off the sphere. If there is friction between the mass and the sphere, does the mass of fly off at a greater or lesser angle than the previous one ?
To solve the problem step by step, we will analyze the motion of the mass m sliding down the frictionless solid sphere and find the angle at which it flies off.
Step 1: Understanding the Forces Acting on the Mass
When the mass m is at an angle θ from the vertical, two forces act on it:
1. The gravitational force mg acting downwards.
2. The normal force N acting perpendicular to the surface of the sphere.
Step 2: Setting Up the Equations of Motion
As the mass slides down, it moves in a circular path. The centripetal force required for this circular motion is provided by the component of the gravitational force acting towards the center of the sphere minus the normal force.
At angle θ:
- The component of gravitational force acting towards the center is mgcosθ.
- The centripetal force required is mv2R, where v is the speed of the mass at angle θ.
Step 3: Applying the Force Balance Equation
At the point of flying off the sphere, the normal force N becomes zero. Therefore, we can write the force balance equation as:
mgcosθ=mv2R
Step 4: Relating Velocity to Height
Since the mass starts from rest and slides down the sphere, we can use conservation of energy to relate the potential energy at the top to the kinetic energy at angle θ:
mgh=12mv2
Here, h=R(1−cosθ) is the height lost when the mass descends to angle θ. Thus,
mgR(1−cosθ)=12mv2
From this, we can express v2:
v2=2gR(1−cosθ)
Step 5: Substituting for Velocity in the Force Equation
Substituting v2 into the force balance equation gives:
mgcosθ=m2gR(1−cosθ)R
This simplifies to:
gcosθ=2g(1−cosθ)
Dividing both sides by g (assuming g≠0):
cosθ=2(1−cosθ)
This can be rearranged to:
cosθ+2cosθ=2
3cosθ=2
Thus,
cosθ=23
Step 6: Finding the Angle θ
To find the angle θ:
θ=cos−1(23)
Step 7: Considering the Effect of Friction
If there is friction between the mass and the sphere, the frictional force acts in the direction of motion, providing additional centripetal force. This means that the mass will require a lesser angle to maintain circular motion before flying off. Therefore, the mass will fly off at a greater angle than the previous one.
Summary of Results
- The angle at which the mass flies off the sphere is θ=cos−1(23).
- If friction is present, the mass will fly off at a greater angle than without friction.
When the mass m is at an angle θ from the vertical, two forces act on it:
1. The gravitational force mg acting downwards.
2. The normal force N acting perpendicular to the surface of the sphere.
As the mass slides down, it moves in a circular path. The centripetal force required for this circular motion is provided by the component of the gravitational force acting towards the center of the sphere minus the normal force.
- The component of gravitational force acting towards the center is mgcosθ.
- The centripetal force required is mv2R, where v is the speed of the mass at angle θ.
At the point of flying off the sphere, the normal force N becomes zero. Therefore, we can write the force balance equation as:
mgcosθ=mv2R
Since the mass starts from rest and slides down the sphere, we can use conservation of energy to relate the potential energy at the top to the kinetic energy at angle θ:
mgh=12mv2
Here, h=R(1−cosθ) is the height lost when the mass descends to angle θ. Thus,
mgR(1−cosθ)=12mv2
From this, we can express v2:
v2=2gR(1−cosθ)
Substituting v2 into the force balance equation gives:
mgcosθ=m2gR(1−cosθ)R
This simplifies to:
gcosθ=2g(1−cosθ)
Dividing both sides by g (assuming g≠0):
cosθ=2(1−cosθ)
This can be rearranged to:
cosθ+2cosθ=2
3cosθ=2
Thus,
cosθ=23
To find the angle θ:
θ=cos−1(23)
If there is friction between the mass and the sphere, the frictional force acts in the direction of motion, providing additional centripetal force. This means that the mass will require a lesser angle to maintain circular motion before flying off. Therefore, the mass will fly off at a greater angle than the previous one.
- The angle at which the mass flies off the sphere is θ=cos−1(23).
- If friction is present, the mass will fly off at a greater angle than without friction.
Topper's Solved these Questions
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 1 (FROM BANKING OR RAILS AND ROADS)
Explore 13 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 2 (CONCEPTUAL SHORT ANSWERS QUESTIONS WITH ANSWERS)
Explore 14 Videos
- CIRCULAR MOTION Book:ICSEChapter:CIRCULAR MOTION Exercise:MODULE 1 (FROM ANGULAR VELOCITY)
Explore 4 Videos
- COMPETITION CARE UNITBook:ICSEChapter:COMPETITION CARE UNITExercise:OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
Explore 50 Videos
Similar Questions
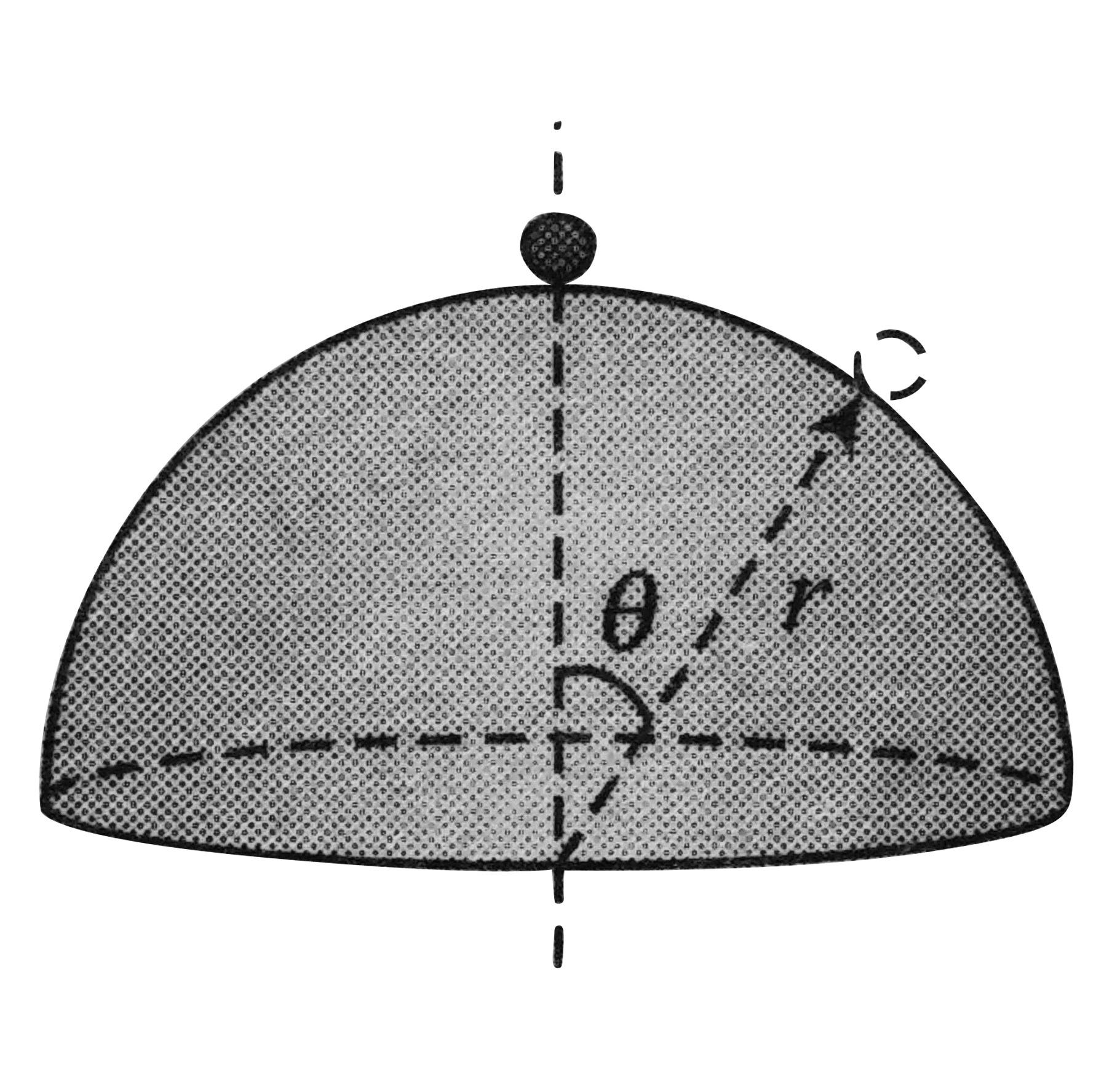
A point mass m starts from rest and slides down the surface of a frictionless hemisphere of radius r as shown figure. Measure angle from the vertical and potential energy from the top. Find
a. Find the changes in potential energy of the mass with angle
b. Find the kinetic energy as a function of angle
c. Find the radial and tangential acceleration as a function of angle
d. Find the angle at which the mass files off the hemisphere
e. If there is friction between the mass and hemisphere, does the mass fly off at a greater or lesser angle than in part (d) ?
View SolutionA chain of length l and mass m lies on the surface of a smooth sphere of radius R>l with one end tied to the top of the sphere.
View Solution
Knowledge Check
Find the moment of inertia of a sphere about a tangent to the sphere, while the mass of the sphere is M and the radius of the sphere is R.
A25MR2B65MR2C45MR2D75MR2
A particle of mass m starts to slide down from the top of the fixed smooth sphere. What is the tangential acceleration when it break off the sphere ?
View SolutionFind the moment of inertia of a sphere about a tangent to the sphere, while the mass of the sphere is M and the radius of the sphere is R.
View SolutionA disc and a solid sphere of same mass and radius roll down an inclined plane. The ratio of thhe friction force acting on the disc and sphere is
View SolutionA small mass m starts from rest and slides down the smooth spherical surface of F. Assume zero potential energy at the top. Find
(a) the change in potential energy,
(b) the kinetic energy,
(c) the speed ot the mass as a function of the angle θ made by the radius through the mass with the vertical.
View SolutionA hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . They y -coordinate of the centre of mass of the remaining sphere is

View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping. Force of friction between sphere and plank is

View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.
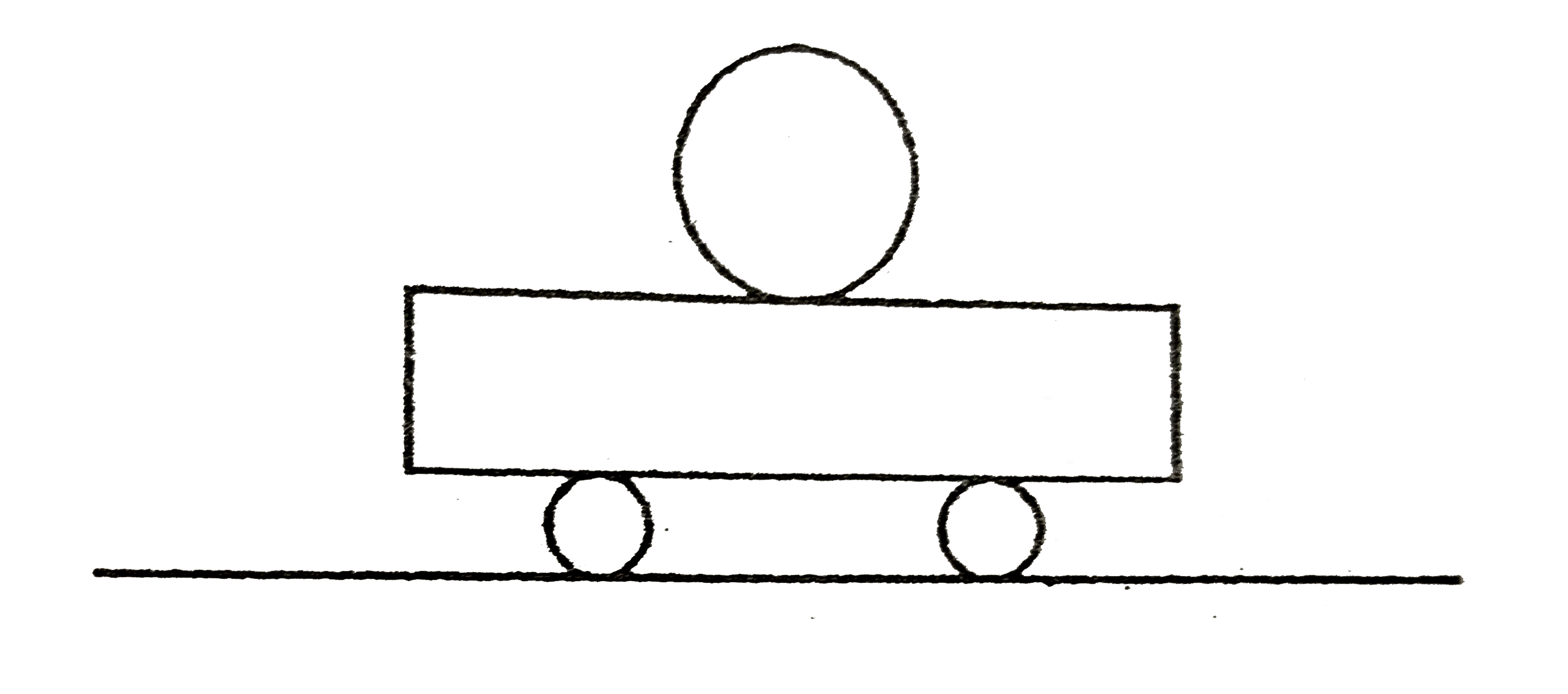
Acceleration of centre of mass of sphere is
View Solution