A hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . They y -coordinate of the centre of mass of the remaining sphere is

YCM=−R15
YCM=−R40
YCM=−R30
YCM=−R20
The correct Answer is:B
Step by step video & image solution for A hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . They y -coordinate of the centre of mass of the remaining sphere is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A hemi-spherical cavity is created in solid sphere (of radius 2R) as shown in the figure. Then

View SolutionThe radius of gyration of a solid sphere of radius R about its tangent is
View SolutionA particle of mass m is placed at a distance of 4R from the centre of a huge uniform sphere of mass M and radius R. A spherical cavity of diameter R is made in the sphere as shown in the figure. If the gravitational interaction potential energy of the system of mass m and the remaining sphere after making the cavity is λGMm28R. Find the value of λ
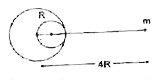
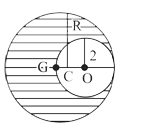
View SolutionAs shown in figure, when a spherical cavity (centered at O) of radius 2 is cut out of a uniform sphere of radius R (centered at C), the centre of mass of remaining (shaded) part of sphere is at G, i.e, on the surface of the cavity. R can be determined by the equation:
View SolutionDetermine the centre of mass of a uniform hemisphere of radius R.
View SolutionA solid of radius 'R' is uniformly charged with charge density ρ in its volume. A spherical cavity of radius R2 is made in the sphere as shown in the figure. Find the electric potential at the centre of the sphere.

View SolutionA cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R/2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM/R2, where M is the mass of the solide sphere]
View SolutionA cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R/2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM/R2, where M is the mass of the solide sphere]
View Solution
consider a neutral conducting sphere of radius a with a spherical cavity of radius b. A charged conducting sphere of radius c is placed in cavity . Centre of this sphere coincide with centre of cavity charge on the inner sphere is q total self energy of this arrangement is:
View SolutionA spherical hole is made in a solid sphere of radius R. The mass of the sphere before hollowing was M. The gravitational field at the centre of the hole due to the remaining mass is

View Solution
