A small smooth ball is placed on a smooth circular disc when the disc is rotated the ball falls down. Why ?
To understand why the small smooth ball falls off the smooth circular disc when it is rotated, we can break down the explanation into several steps:
Step 1: Understanding the System
- We have a small smooth ball placed on a smooth circular disc. The disc is capable of rotating about its center.
Step 2: Rotation of the Disc
- When the disc starts to rotate, the ball experiences a tendency to move outward due to inertia. This is because the ball wants to maintain its state of rest (Newton's first law of motion) while the disc is moving.
Step 3: Centripetal Force Requirement
- For an object to move in a circular path, a centripetal force is required. This force is directed towards the center of the circular path. The formula for centripetal force is given by:
Fc=mv2r
where m is the mass of the ball, v is the tangential velocity, and r is the radius of the circular path.
Step 4: Absence of Friction
- In this scenario, the surface of the disc is smooth, which means there is no frictional force acting on the ball. Friction is what would typically provide the necessary centripetal force to keep the ball moving in a circular path.
Step 5: Resulting Motion of the Ball
- Since there is no friction to provide the required centripetal force, the only force acting on the ball is the outward inertial force (often referred to as the centrifugal force in a rotating frame). This force causes the ball to move outward and eventually fall off the edge of the disc.
Conclusion
- Therefore, the ball falls down because the smooth surface of the disc does not provide the necessary frictional force to keep it in circular motion. Without this force, the ball cannot maintain its circular path and falls off.
- We have a small smooth ball placed on a smooth circular disc. The disc is capable of rotating about its center.
- When the disc starts to rotate, the ball experiences a tendency to move outward due to inertia. This is because the ball wants to maintain its state of rest (Newton's first law of motion) while the disc is moving.
- For an object to move in a circular path, a centripetal force is required. This force is directed towards the center of the circular path. The formula for centripetal force is given by:
Fc=mv2r
where m is the mass of the ball, v is the tangential velocity, and r is the radius of the circular path.
- In this scenario, the surface of the disc is smooth, which means there is no frictional force acting on the ball. Friction is what would typically provide the necessary centripetal force to keep the ball moving in a circular path.
- Since there is no friction to provide the required centripetal force, the only force acting on the ball is the outward inertial force (often referred to as the centrifugal force in a rotating frame). This force causes the ball to move outward and eventually fall off the edge of the disc.
- Therefore, the ball falls down because the smooth surface of the disc does not provide the necessary frictional force to keep it in circular motion. Without this force, the ball cannot maintain its circular path and falls off.
Topper's Solved these Questions
- SELF ASSESSMENT PAPER 5Book:ICSEChapter:SELF ASSESSMENT PAPER 5Exercise:Section-B
Explore 13 Videos
- SELF ASSESSMENT PAPER 5Book:ICSEChapter:SELF ASSESSMENT PAPER 5Exercise:Section-C
Explore 9 Videos
- SELF ASSESSMENT PAPER 4Book:ICSEChapter:SELF ASSESSMENT PAPER 4Exercise:Section-D
Explore 6 Videos
- THERMAL CONDUCTIONBook:ICSEChapter:THERMAL CONDUCTIONExercise:SELECTED PROBLEMS (Taken from the Previous Years ISC, AISSCE, HSSCE various States. Boards Roorke Qns & NCERT text) FROM EXPERIMENT TO DETERMINE K
Explore 2 Videos
Similar Questions
A ball is placed on a compressed spring. When the spring is released, the ball is observed to fly away.

Why does the ball fly away?
View SolutionA small ball of mass m is released in a smooth circular tube as shown in figure. The minimum height h such that bead can complete the circle is
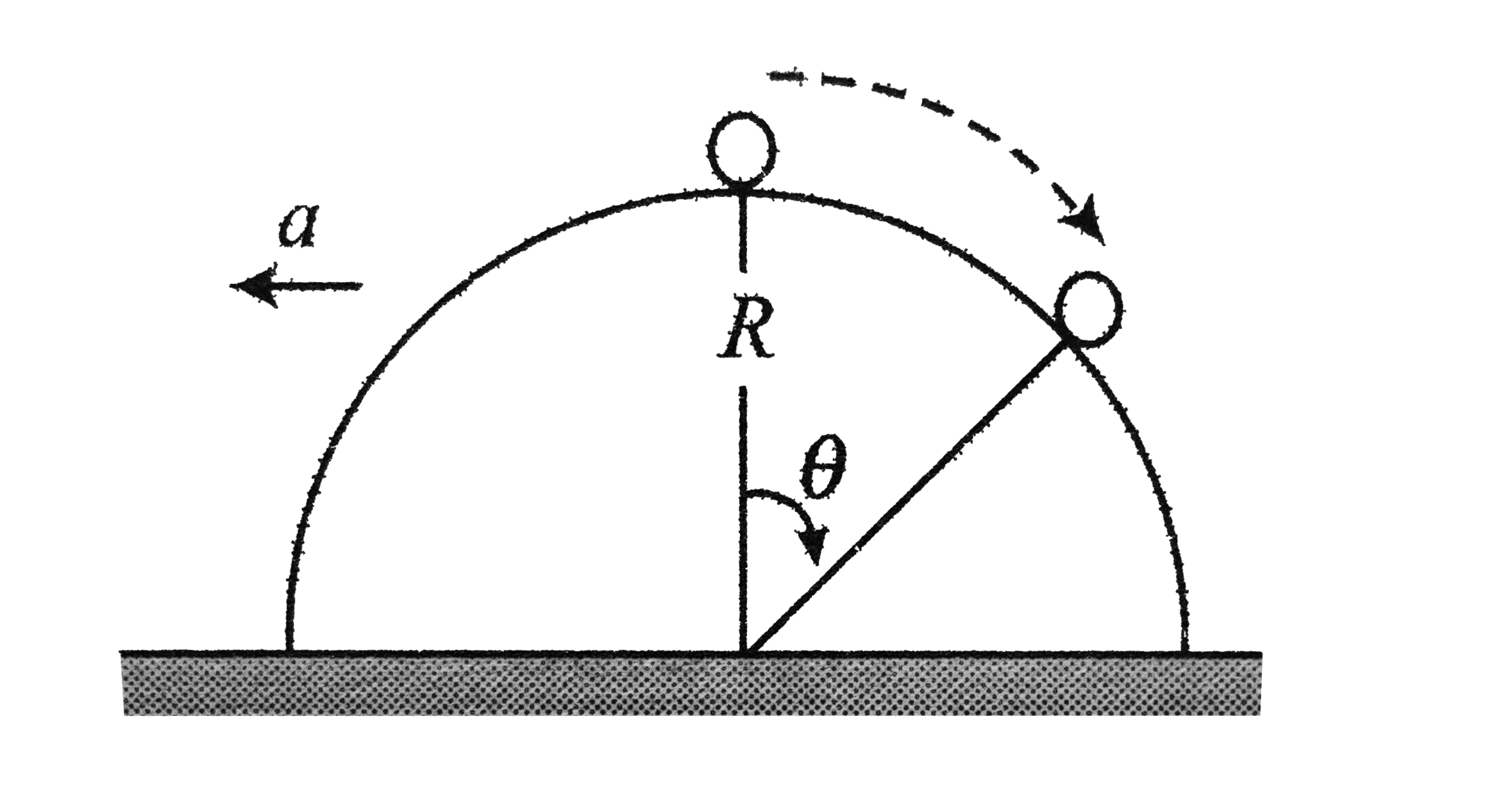
View SolutionA small ball is placed at the top of a smooth hemispherical wedge of radius R. If the wedge is accelerated with an acceleration a, find the velocity of the ball relative to wedge as a function of θ.
View SolutionA uniform disc of mass 'm' and radius R is placed on a smooth horizontal floor such that the plane surface of the disc in contact with the floor . A man of mass m/2 stands on the disc at its periphery . The man starts walking along the periphery of the disc. The size of the man is negligible as compared to the size of the disc. Then the center of disc.

View SolutionA small coin of mass 80g is placed on the horizontal surface of a rotating disc. The disc starts from rest and is given a constant angular acceleration α=2rad/s2. The coefficient of static friction between the coin and the disc is μs=3/4 and cofficient of kinetic friction is μk=0.5. The coin is placed at a distance r=1m from the centre of the disc. The magnitude of the resultant force on the coin exerted by the disc just before it starts slipping on the disc is

View SolutionA small coin of mass 80g is placed on the horizontal surface of a rotating disc. The disc starts from rest and is given a constant angular acceleration α=2rad/s2. The coefficient of static friction between the coin and the disc is μs=3/4 and cofficient of kinetic friction is μk=0.5. The coin is placed at a distance r=1m from the centre of the disc. The magnitude of the resultant force on the coin exerted by the disc just before it starts slipping on the disc is

View SolutionA circular table of radius 0.5m has a smooth diametrical groove. A half of mass 90g is is placed inside the groove along with a spring constant 102Ncm−1 One end of the spring is tied to the table and the other end to the ball The ball is at a distance of .0.1m from the center when the table is at rest On rotating the table with a constant angular frequency of 102rads−1 the ball moves away from the center by a distance nearly equal to
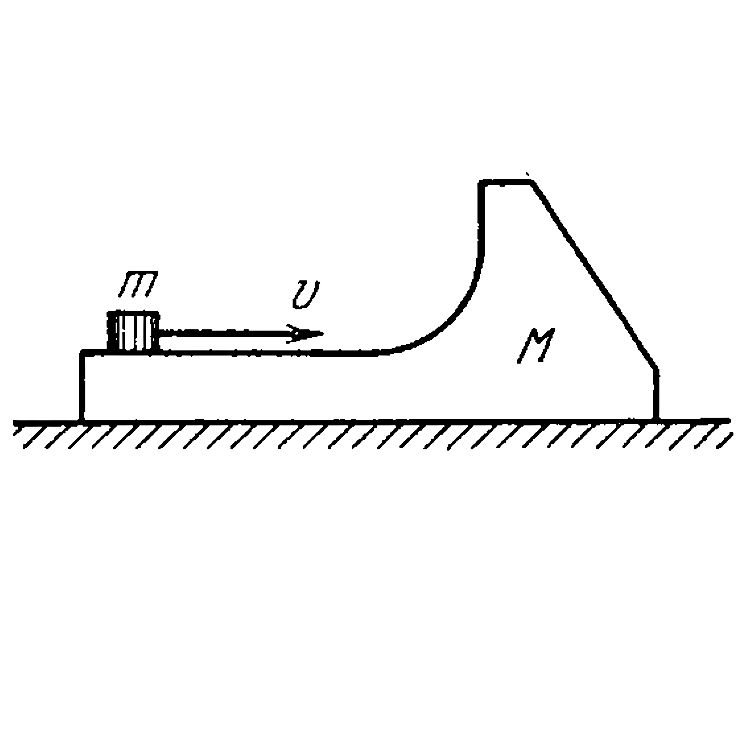
View SolutionA body of mass M (figure) with a small disc of mass m placed on it rests on a smooth horizontal plane. The disc is set in motion in the horizontal direction with velocity v. To what height (relative to the initial level) will the disc rise after breaking off the body M? The friction is assumed to be absent.
View SolutionA string is wrapped on a uniform disc and the other end of the string connected to a wall. The system is placed on a smooth plane, inclined at an angle θ, with the string parallel to the plane, as shown in the figure. The acceleration of the disc is

View SolutionA small coin of mass 40 g is placed on the horizontal surface of a rotating disc. The disc starts from rest and is given a constant angular acceleration α=2 rad s−2. The coefficient of static friction between the coin and the disc is μs=3/4 and the coefficient of kinetic friction is μk=0.5. The coin is placed at a distance r=1m from the centre of the disc. The magnitude of the resultant force on the coin exerted by the disc just before it starts slipping on the disc is?

View Solution