A small sphere of radius r1 and charge q1 is enclosed by a spherical shell of radius r2 and charge q2. Show that if q1 is positive, charge will necessarily flow from the sphere to the shell (when the two are connected by a wire) no matter what the charge q2 on the shell is [Fig]
Electric potential inside the spherical shell is same as that on its surface. When the sphere is kept inside the shell then its potential becomes equal to the potential of the spherical shell. When additional positive charge is given to sphere then its potential increases due to its own charge and hence, it attains potential greater than that of the shell. Thus, when both of them are connected by a metallic wire then all charge of the inner sphere is trasferred to the shell so that both may attain the same potential. The same concept is used in designing a Van de Graaff generator. Charge of the spherical shell of the generator is transferred to it from inside. It is important to note that the pootential of interior conductor will be equl to that of the exterior shell only if charge on the inner sphere is zero.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - NCERT FILE Solved (Additional Exercises) (Answer carefully)
7 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - NCERT FILE Solved (Additional Exercises) (Answer the following)
4 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - NCERT FILE Solved (Textbook Exercise)
11 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
Similar Questions
A small sphere of radius r1 and charge q1 is enclosed by a spherical shell of radius r2 and charge q2. Show that if q1 is positive, charge will necessilly flow from the sphere to the shell (when the two are connected by a wire) no matter what the charge q2 on the shell is [Fig]
View SolutionA small sphere A of radius r and carrying a charge q is enclosed by a concentric spherical shell B of radius 2r carrying a charge 29. When A and B are connected by a conducting wire, the charge will flow from __________ to __________ .
View Solution
Knowledge Check
A metallic sphere of radius R having charge Q is connected to an uncharged sphere of radius 3R. The amount of charge flown through connecting wire is
AQ/4BQ/2C3Q/4DQA spherical conducting shell of radius r0 carry a charge q0. Then value of electric field inside it is :-
Akq0/r2Bkq0/r3CzeroDuniform but non zeroA spherical shell of radius R has a charge +q units. The electric field due to the shell at a point
Ainside is zero and varies as r−1 outside itBinside is constant and varies as r−2Cinside is zero and varies as r−2 outside itDinside is constant and varies as r−1 outside it
A spherical conducting shell of inner radius r1 and outer radius r2 has a charge Q.
(a) A charge q is placed at the centre of the shell. What is the surface charge density on the inner and outer surfaces of the shell ?
View SolutionA conducting sphere of radius R carries a charge Q. It is enclosed by another concentric spherical shell of radius 2R. Charge from the inner sphere is transferred in infinitesimally small installments to the outer sphere. Calculate the work done in transferring the entire charge from the inner sphere to the outer one.
View SolutionA solid metallic sphere of radius R having charge +3Q is surrounded by a hollow spherical shell of radius 2R and having a charge −Q.
(a) Find electric field at distance r from centre of solid sphere [R<r<2R].
(b) Find potential difference between sphere and shell.
(c ) Find distribution of charge if
(i) inner sphere is earthed
(ii) inner sphere and shell are connected by a metallic wire.
View SolutionTwo conducting hollow spherical shells of radius R and 2R carry charges -Q and 3Q respectively. How much charge will flow into the earth if inner shell is grounded?
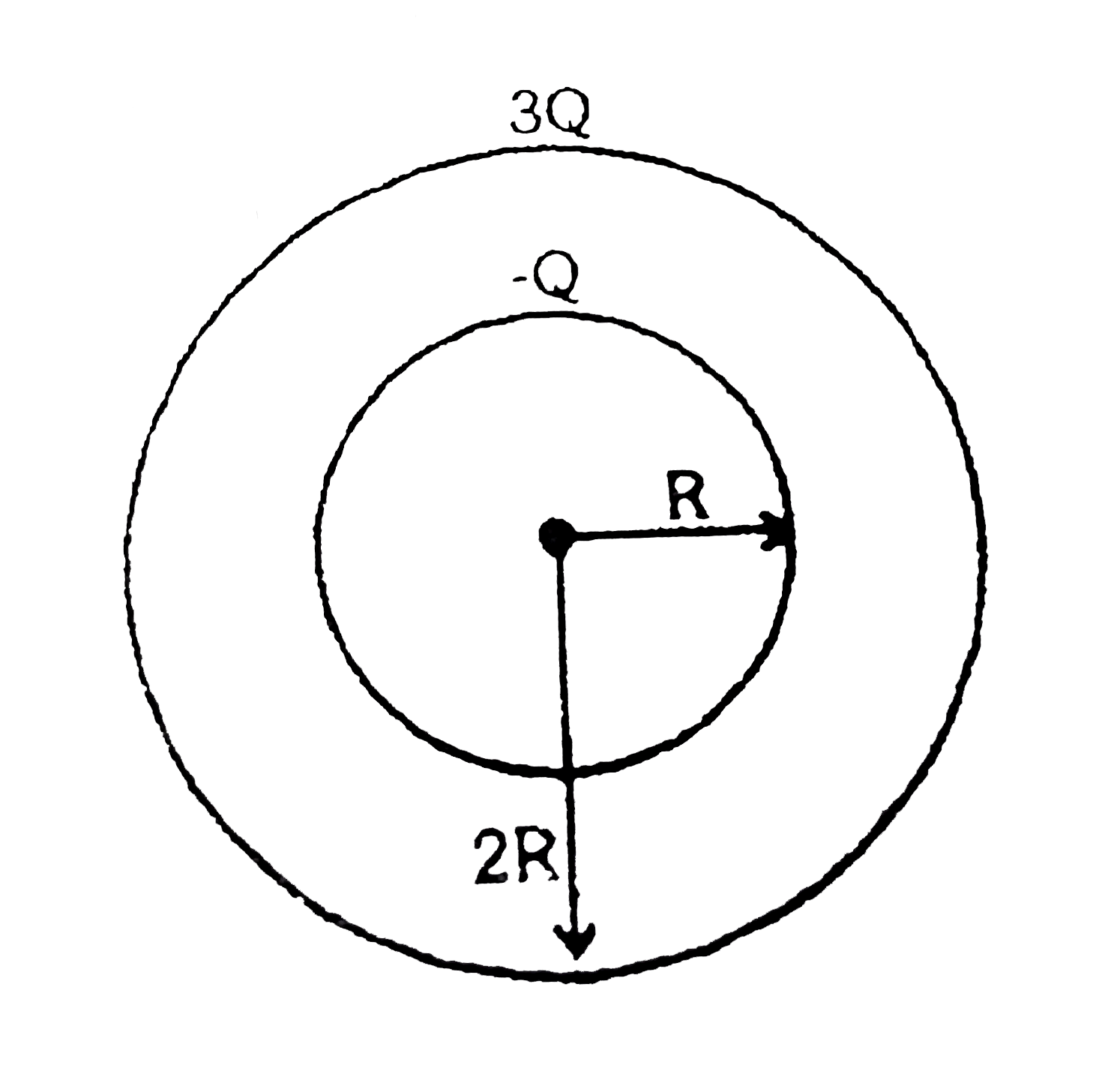
View SolutionA solid conducting sphere of radius 10cm is enclosed by a thin metallic shell of radius 20cm. A charge q=20μC is given to the inner sphere is connected to the shell by a conducting wire.
View Solution
