A small spherical monoatomic ideal gas bubble (γ=5/3) is trapped inside a liquid of density ρ (see figure). Assume that the bubble does not exchange any heat with the liquid. The bubble contains n moles of gas. The temperature of the gas when the bubble is at the bottom is T0, the height of the liquid is H and the atmospheric pressure P0 (Neglect surface tension).
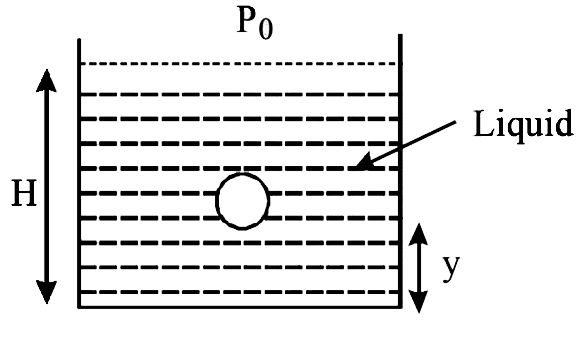
The buoyancy force acting on the gas bubble is (Assume R is the universal gas constant)
ρ1nRgT0(P0+ρlgH)25(P0+ρ1gy)75
ρlnRgT0(P0+ρlgH)25[P0+ρlg(H−y)]35
ρ1nRgT0(P0+ρ1gH)35(P0+ρlgy)85
ρ1nRgT0(P0+ρlgH)35[P0+ρlg(H−y)]25
The correct Answer is:B
Buoyancy force F= (volume of bubble)(ρ1)g
=(nRT2p2)ρ1g
Here T2=⎡⎢⎣p0+peg(H−y)(p0+ρ1gh)25⎤⎥⎦
and p2=p0+ρ1g(H−y)
Substituting the values we get
F=ρlnRgT0(p0+plgH)25[p0+ρlg(H−y)]35
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - MCQ_TYPE
3 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
A small spherical monoatomic ideal gas bubble (γ=5/3) is trapped inside a liquid of density ρ (see figure). Assume that the bubble does not exchange any heat with the liquid. The bubble contains n moles of gas. The temperature of the gas when the bubble is at the bottom is T0, the height of the liquid is H and the atmospheric pressure P0 (Neglect surface tension).

When the gas bubble is at a height y from the bottom, its temperature is-
View SolutionA small spherical monoatomic ideal gas bubble (γ=53) is trapped inside a liquid of density ρl (see figure) . Assume that the bubble does not exchange any heat with the liquid. The bubble contains n moles of gas. The temperature of the gas when the bubble is at the bottom is T0, the height of the liquid is H and the atmospheric pressure is P0 (Neglect surface tension).
_E01_434_Q01.png)
When the gas bubble is at a height y from the bottom , its temperature is :-
View Solution
Knowledge Check
The pressure inside a liquid of density ρ at a depth h is :
AhρgBhρgChρgDhρWhen a large bubble rises from the bottom of a lake to the surface, its radius doubles, The atmospheric pressure is equal to that of a column of water of height H. The depth of the lake is
AHB2 HC7 HD8 HThe pressure at depth h below the surface of a liquid of density ρ open to the atmosphere is
Agreater than the atmospheric pressure by ρghBless than the atmospheric pressure by ρghCequal to the atmospheric pressureDincreases exponentially with depth
A small spherical monoatomic ideal gas bubble (γ=5/3) is trapped inside a liquid of density ρ (see figure). Assume that the bubble does not exchange any heat with the liquid. The bubble contains n moles of gas. The temperature of the gas when the bubble is at the bottom is T0, the height of the liquid is H and the atmospheric pressure P0 (Neglect surface tension).
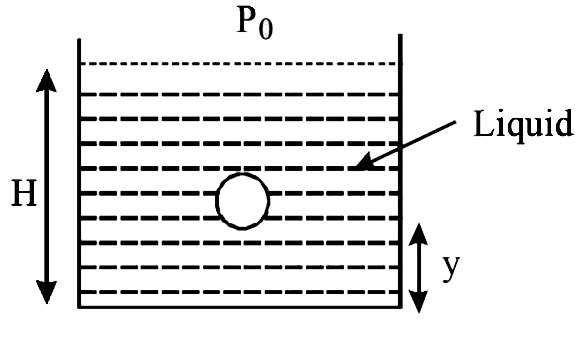
As the bubble moves upwards, besides the buoyancy force the following forces are acting on it
View SolutionA small spherical monoatomic ideal gas bubble (γ=5/3) is trapped inside a liquid of density ρ (see figure). Assume that the bubble does not exchange any heat with the liquid. The bubble contains n moles of gas. The temperature of the gas when the bubble is at the bottom is T0, the height of the liquid is H and the atmospheric pressure P0 (Neglect surface tension).

As the bubble moves upwards, besides the buoyancy force the following forces are acting on it
View SolutionThe gas inside a spherical bubble expands uniformly and slowly so that its radius increases from R to 2R. Let the atmospheric pressure be p0 and surface tension be S. The work done by the gas in the process is
View SolutionA metal sphere connected by a string is dipped in a liquid of density ρ as shown in figure. The pressure at the bottom of the vessel will be, (p0=atmospheric pressure )

View SolutionThe time period of a soap bubble is T which depneds on pressure p density d and surface tension s then the relation for T is
View Solution
