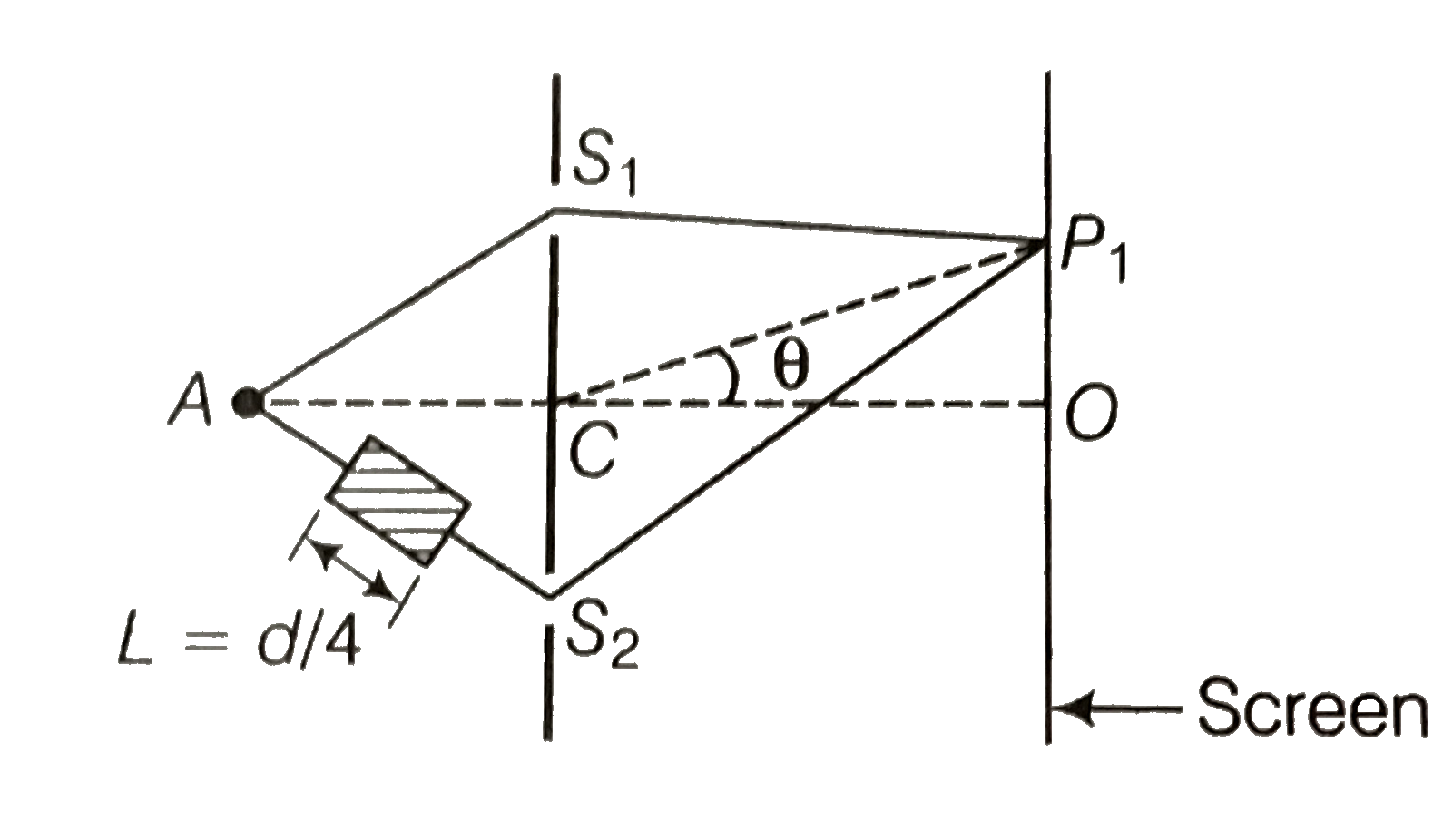
A small transparent slab containing material of μ=1.5 is placed along AS2(figure). What will be the distance from O of the principle maxima and of the first minima on either side of the principal maxima obtained in the absence of the glass slab ?
0.19 D and -0.33 D
0.19 D and -0.55 D
0.33 D and -0.65 D
0.33 D and -0.75 D
The correct Answer is:A
Step by step video, text & image solution for A small transparent slab containing material of mu=1.5 is placed along AS_(2)(figure). What will be the distance from O of the principle maxima and of the first minima on either side of the principal maxima obtained in the absence of the glass slab ? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - NCERT FINGERTIPSCHAPTER - WAVE OPTICSEXERCISE - Diffraction22videos
WAVE OPTICS
- BOOK - NCERT FINGERTIPSCHAPTER - WAVE OPTICSEXERCISE - Polarisation18videos
WAVE OPTICS
- BOOK - NCERT FINGERTIPSCHAPTER - WAVE OPTICSEXERCISE - Coherent And Incoherent Addition Of Waves7videos
WAVE OPTICS
- BOOK - NCERT FINGERTIPSCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS EXERCISE - Assertion And Reason15videos
SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS
Similar Questions
Light of wavelength 6×10−5 cm falls on screen at a distance of 100 cm from a narrow slit. Find the width of the slit if the first minima lies 1mm on either side of the central maximum
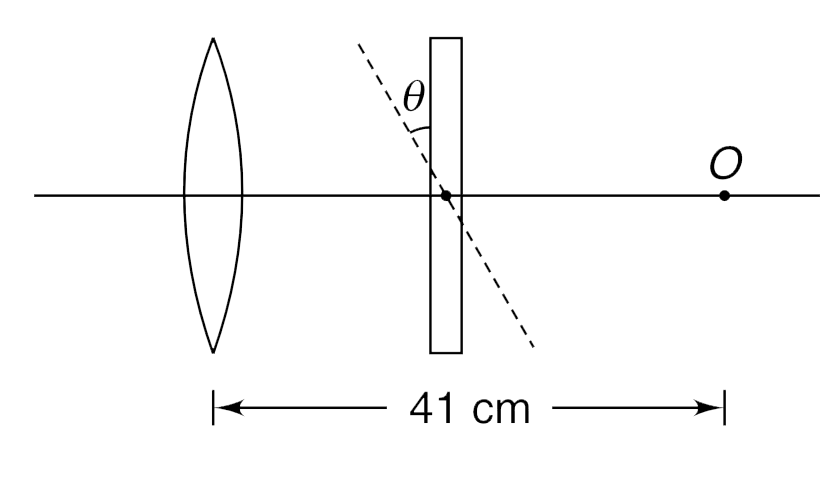
View SolutionA point object O is placed at a distance of 41 cm from a convex lens of focal length f=20 cm on its principal axis. A glass slab of thickness 3 cm and refractive index μ=1.5 is placed between the lens and the object with its faces perpendicular to the principal axis of the lens. Image of the object is formed at point I1. Now the glass slab is tilted by an angle of θ=1° (as shown in the Figure) and the final image is formed at I2. Calculate the distance between points I1 and I2. Consider only paraxial rays for the lens and near normal incidence for the glass slab.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A small transparent slab (μ=1.5) is placed along AS2 as shown.

AC=CO=D,S1C=S2S=d<<D
The distance of princpal maxima front 'O' isAD4BD16CD8DD - Question 2 - Select One
A small transparent slab (μ=1.5) is placed along AS2 as shown.

AC=CO=D,S1C=S2S=d<<D
The distance of first minima below the point O isAD√231B3D√231C2D√231D5D√231 - Question 3 - Select One
A small transparent slab (μ=1.5) is placed along AS2 as shown.

AC=CO=D,S1C=S2S=d<<D
The distance of first minima above O isA3D√43BD√247C3D√247D5D√247
Light of wavelengthλ=500nm falls on two narrow slits placed a distance d = 50×10−4 cm
apart, at an angle ϕ=30∘ relative to the slits as shown in figure. On the lower slit a transparent slab of thickness 0.1 mm and refractive index 32 is placed. The interference pattern is observed at a distance D=2m from the slits. Then, calculate

(a) position of the central maxima.
(b) the order of maxima at point C of screen .
(c)how many fringes will pass C, if we remove the transparent slab from the lower slit?View SolutionA Franhoffer diffraction pattern due to a single slit of width 0.2 mm is being obtained on a screen placed at a distance of 2 m from the slit. The first minima lie at 5mm in either side of the centre maximum on the screen. Find the wavelength of the light used .
View SolutionIn the diffraction from a single slit of width 2.5λ, the total number of minimas and secondary maximum (maxima) on either side of the central maximum are
View SolutionIn the diffraction from a single slit of width 2.5λ, the total number of minimas and secondary maximum (maxima) on either side of the central maximum are
View SolutionIn YDSE arrangement as shown in figure, fringes are seen on screen using monochromatic source S having wavelength 3000 Å (in air). S1and S2 are two slits seperated by d = 1 mm and D = 1m. Left of slits S1 and S2 medium of refractive index n1=2 is present and to the right of S1 and S2 medium of n2=32, is present. A thin slab of thickness 't' is placed in front of S1 . The refractive index of n3 of the slab varies with distance from it's starting face as shown in figure.

In order to get central maxima at the centre of screen, the thickness of slab required is :View Solution

