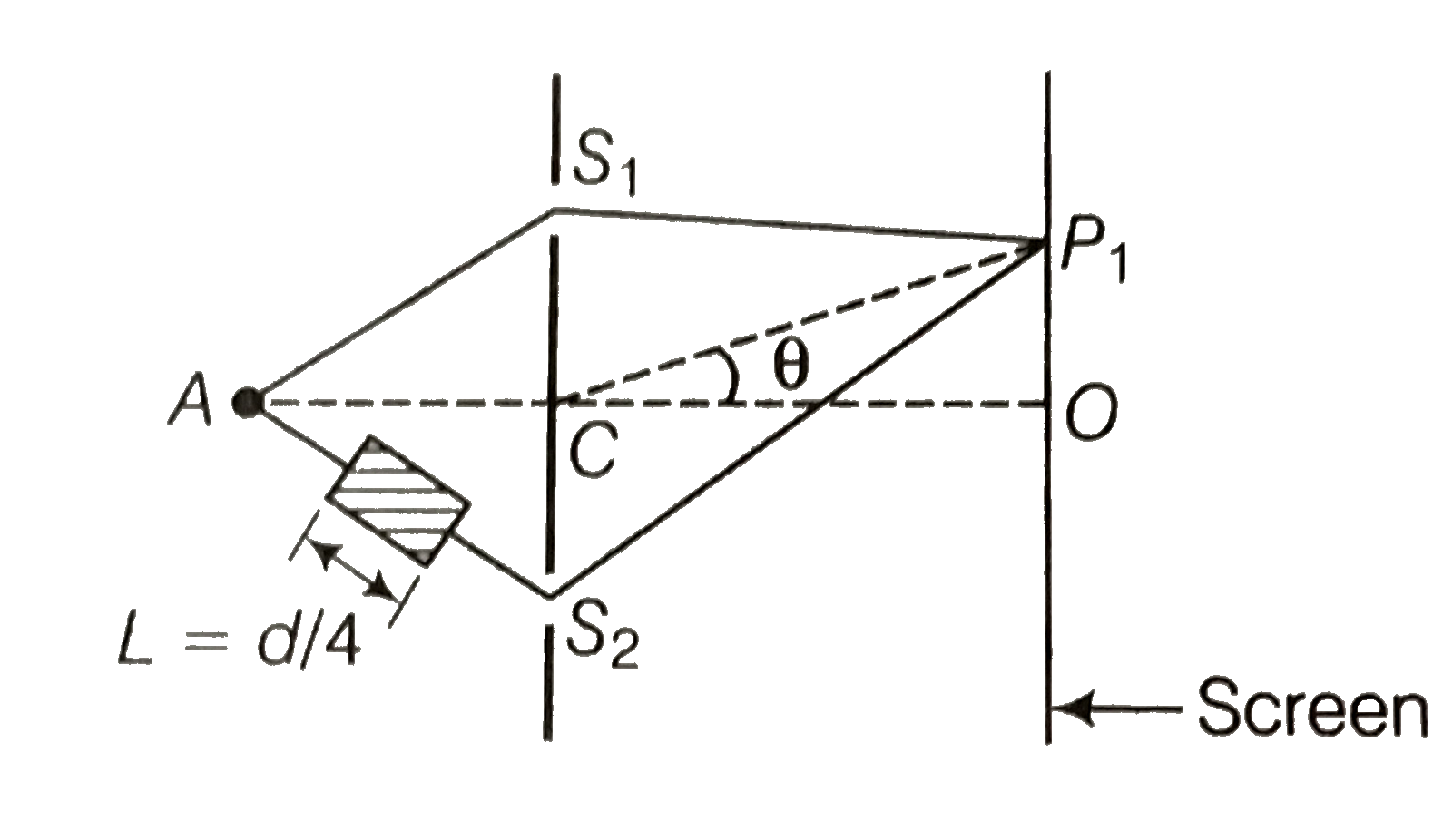
A small transparent slab containing material of μ=1.5 is placed along AS2(figure). What will be the distance from O of the principle maxima and of the first minima on either side of the principal maxima obtained in the absence of the glass slab ?
In case of transparent glass slabe of refractive indesx μ, the path difference will be calculated as Δx=2dsinθ+(μ−1)L
In case of transparent glass slab of refractive index μ,
the path difference =2dsinθ+(μ−1)L.
For the principal maxima, (path difference is zero )
i.e., 2dsinθ0+(μ−1)L=0
or, sinθ0=−L(μ−1)2d=−L(0.5)2d [∴L=d/4]
or sinθ0=−616
∴OP=Dtanθ0≈Dsinθ0=−D16
For the first minima, the path difference is ±λ2
∴2dsinθ1+0.5L=±λ2
or sinθ1=±λ/2−0.5L2d=±λ/2−d/82d
=±λ/2−λ/82λ=±14−116
[∴ The diffraction occurs if the wavelength of waves in nearly equal to the side width (d)]
On the positive side sinθ'+1=+14−116=316
On the negative side sinθ''−1=−14−116=−516
The First principal maxima on the positive side is at distance
Dtanθ'+1=Dsinθ'+1√1−sin2θ'1=D3√162−32=3D√247 above point O
The first principal minima on the negative side is at distance
Dtanθ''1=5D√162−52=5D√231 below point O.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Short answer type Questions3videos
WAVE OPTICS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIAL,DEVICES AND SIMPLE CIRCUITEXERCISE - Multiplel choice questions26videos
SEMICONDUCTOR ELECTRONICS: MATERIAL,DEVICES AND SIMPLE CIRCUIT
Similar Questions
Light of wavelength 6×10−5 cm falls on screen at a distance of 100 cm from a narrow slit. Find the width of the slit if the first minima lies 1mm on either side of the central maximum
View SolutionLight of wavelengthλ=500nm falls on two narrow slits placed a distance d = 50×10−4 cm
apart, at an angle ϕ=30∘ relative to the slits as shown in figure. On the lower slit a transparent slab of thickness 0.1 mm and refractive index 32 is placed. The interference pattern is observed at a distance D=2m from the slits. Then, calculate

(a) position of the central maxima.
(b) the order of maxima at point C of screen .
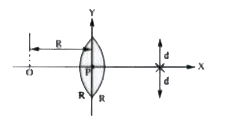
(c)how many fringes will pass C, if we remove the transparent slab from the lower slit?View SolutionA biconvex thin lens of radius of curvature R is made up of variable refractive index μ=2(1+rd). Assume 2d<<R. There are infinite images of the point O, which is placed at a distance R on the principal axis from the lens as shown in the figure. The image is spread along the pricipal axis in a length of (r is the radial distance from P measured perpendicular to principal axis)
 View Solution
View SolutionIn YDSE arrangement as shown in figure, fringes are seen on screen using monochromatic source S having wavelength 3000 Å (in air). S1and S2 are two slits seperated by d = 1 mm and D = 1m. Left of slits S1 and S2 medium of refractive index n1=2 is present and to the right of S1 and S2 medium of n2=32, is present. A thin slab of thickness 't' is placed in front of S1 . The refractive index of n3 of the slab varies with distance from it's starting face as shown in figure.

In order to get central maxima at the centre of screen, the thickness of slab required is :View SolutionAn object is placed 21 cm in fron of a concave mirror of radius of curvature 20 cm.A glass slab of thicknes 3 cm and refractive index 1.5 is palced close to the mirror in the space between the object and the mirror. Find the position of the final image fromed. The distance of the nearer surface of the slab from the mirror is 10 cm.
 View Solution
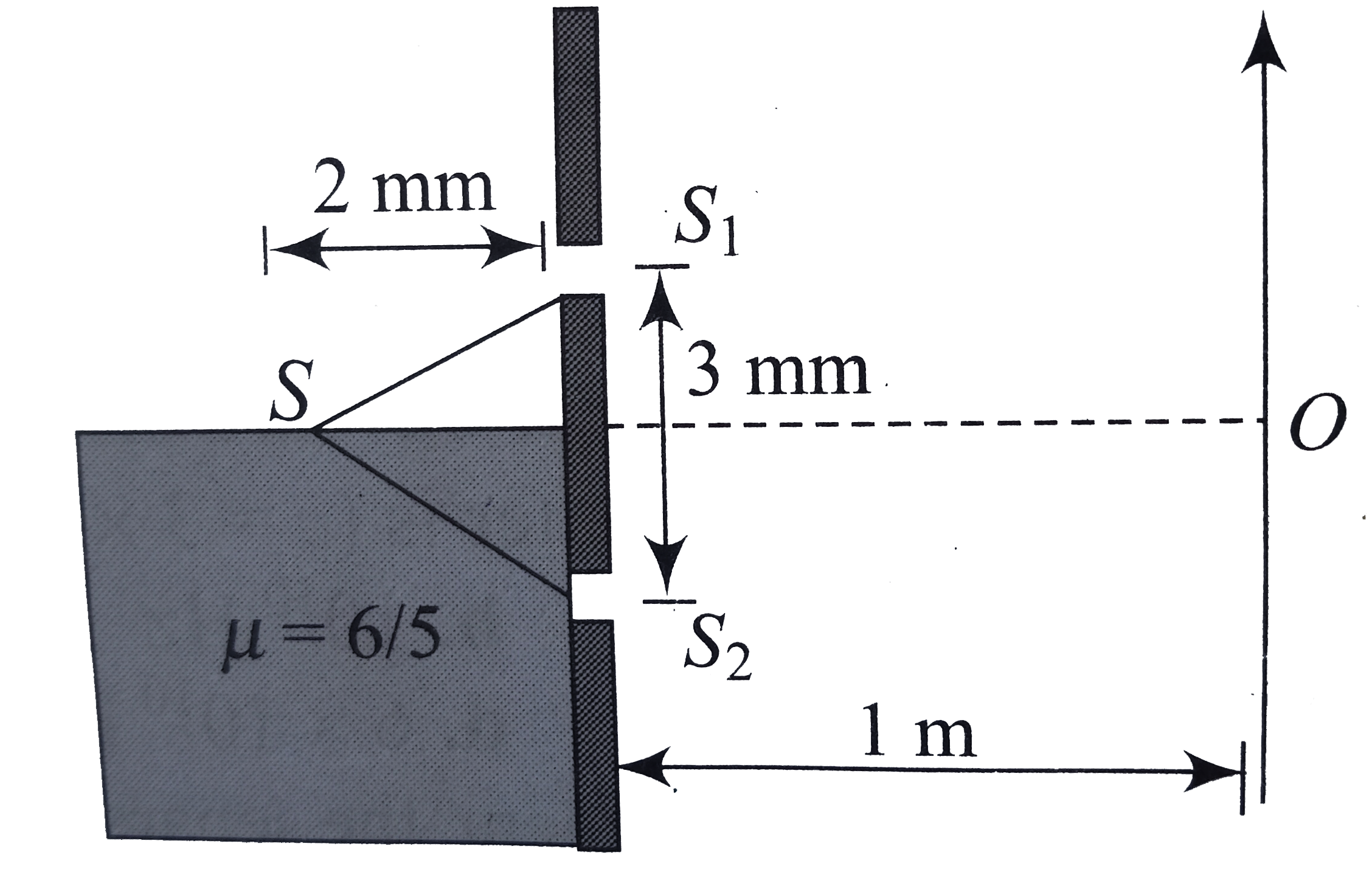
View SolutionIn Young's double-slit experiment, a point source is placed on a solid slab of refractive index 6/5 at a distance of 2 mm from two slits spaced 3 mm apart as shown and at equal distacne from both the slits. The screen is at a distance of 1 m from the slits. Wavelength of light used is 500 nm.
a. Find the position of the central maximum.
b. Find the order of the fringe formed at O.
c. A film of refractive index 1.8 is to be placed in front of S1 so that central maxima is formed where 200th maxima was formed. Find the thickness of film.
 View Solution
View SolutionA transparent cube contains a small air bubble. Its apparent distance is 2 cm when seen through other facel. If the refractive index of the material of the cube is 1.5, the real length of the edge of cube must be
View SolutionA point object is placed on the principal axis of a convex lens (f = 15 cm) at a distance of 30 cm from it. A glass plate (μ=1.50) of thickness 1 cm is placed on the other side of the lens perpendicular to the axis. Locate the image of the point object.
View SolutionThe figure ,shows a transparent sphere of radiusRand refractive indexμ.An object Ois placed at a distance x from the pole of the first surface so that a real image is formed at the pole of the exactly opposite surface.
 if an object is Placed at a distanceR from the pole of first surface ,then the real image is formed at a distance Rfrom thepole of the second surface.The refractive indexμ of the spher is given byView Solution
if an object is Placed at a distanceR from the pole of first surface ,then the real image is formed at a distance Rfrom thepole of the second surface.The refractive indexμ of the spher is given byView SolutionA monochromatic light of λ=500nm is incident on two identical slits separated by a distance of 5×10−4m. The interference pattern is seen on a screen placed at a distance of 1m from the plane of slits. A thin glass plate of thickness 1.5×10−6m and refractive index μ=1.5 is placed between one of the slits and the screen. Find the intensity at the center of the screen if the intensity is I0 in the absence of the plate. Also find the lateral shift of the central maxima and number of fringes crossed through center.
View Solution

