A soap bubble of radius r and surface tension T is given a potential V. Show that the new radius R of the bubble is related with the initial radius by the equation
where P is the atmospheric pressure.
The correct Answer is:A
Here,
or, .
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Example 13.1
1 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Example 13.2
1 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Level 2 Comprehension Based
7 Videos
- EXPERIMENTSBOOK - DC PANDEYCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A soap bubble of radius 'r' and surface tension 'T' is given a potential of 'V' volt. If the new radiys 'R' of the bubble is related to its initial radius by equation.
P0[R3−r3]+[λT[R2−r2]−ε0V2R/2=0, where P0 is the atmospheric pressure. Then find λ
View SolutionTwo soap bubbles of radius R1 and R2 combine isothermally to form a new soap bubble. Find radius of new soap bubble
View Solution
Knowledge Check
The excess pressure inside a soap bubble P and the radius R of the bubble are related as
Ap∝1/RBP∝RCP∝R2DP∝1/R2Excess pressure inside a soap bubble of radius r and surface tension T is
A2TrB4TrCT2rDT4rA soap bubble of radius r is placed on another bubble of radius 2r. The radius of the surface common to both the bubbles is
A2r3B3rC2rDr
Two soap bubble of radius 2r and 3r are in contact with each other. If the radius of curvature of the interface between the bubble in nr then find the value of n:
View SolutionWhat is the surface energy of a soap bubble of radus r and surface tension T?
View SolutionA soap bubble of radius r and surface tension constant T is given a charge, so that its surface charge density is σ. Due to charge, the radius os the soap bubble becomes double then find 'σ'. (atmospheric pressure =P0)
View SolutionTwo soap bubbles of radii r1andr2 are attached as shown. Find the radius of curvature of the common film ACB.
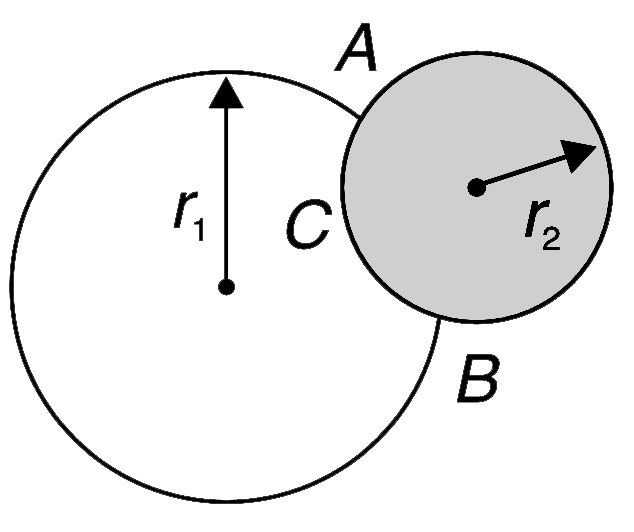
View SolutionIf the radius and surface tension of a spherical soap bubble are 'R' and 'T' respectively, Then show that the charge required to double its radius would be 8πR,[ε0R[7p0R+12T]]12. Where p0 is the atmospheric pressure.
View Solution
