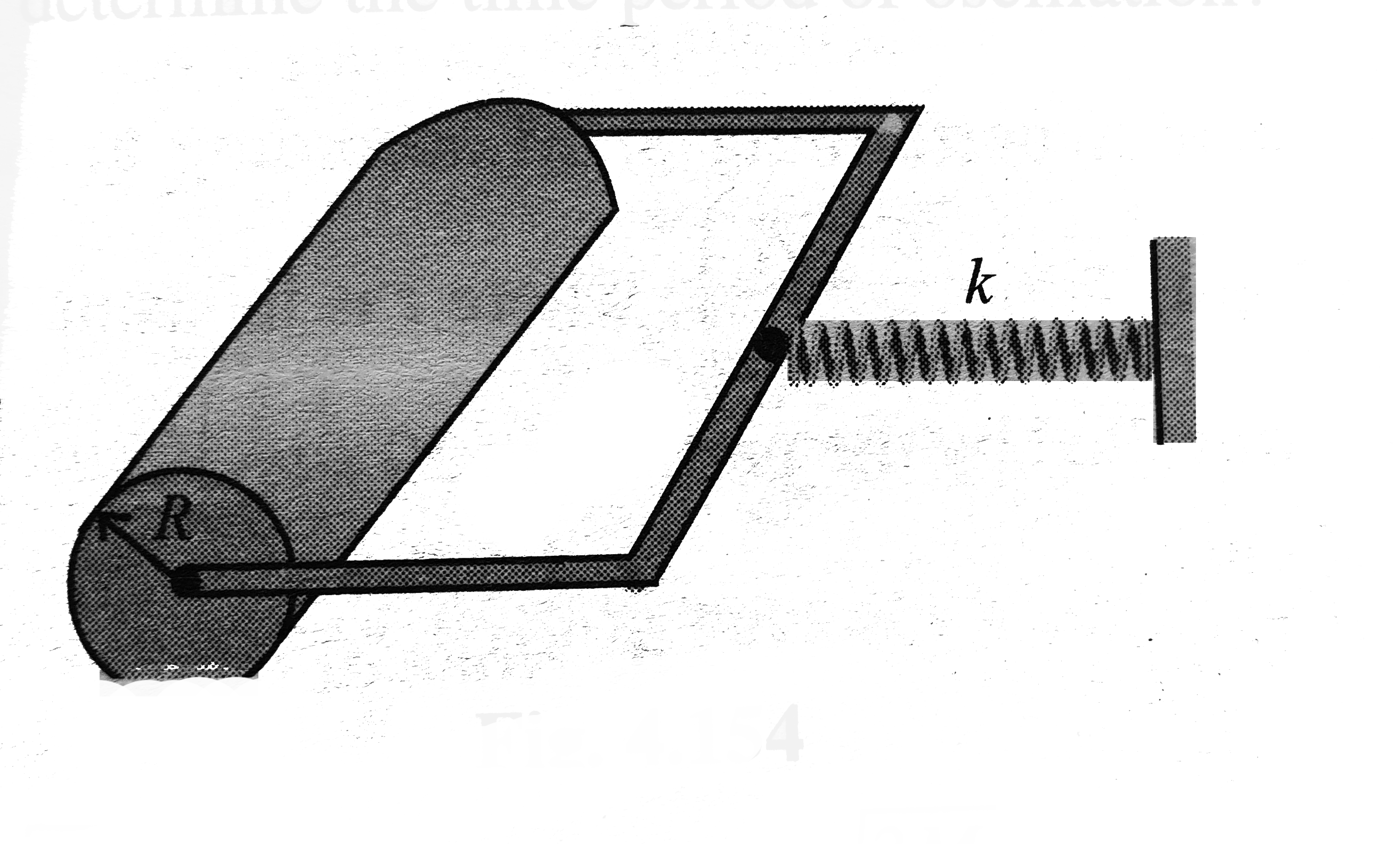
A soil cylinder of mass M and radius R is connected to a spring as shown in fig. The cylinder is placed on a rough horizontal surface. All the parts except the cylinder shown in the figure are light. If the cylinder is displaced slightly from its mean position and released, so that it performs pure rolling back and forth about its equilibrium position, determine the time period of oscillation?
(a)2π√Mk
(b)2π√3M2k
(c)2π√3Mk
(d)none of these
The correct Answer is:B
Let us say in displaced position, the axis of cylinder is at a distance x from its mean position and its velocity of center of mass if x and angular velocity is ω. Then, as cylinder is not slipping v=Rω. In this position the spring elongates by x. Using energy method we can find frequency of oscillation very easily.
Total energy of oscillation is
E=Iω22+Mv22+kx22
We have I=MR22, so E=34Mv2+kx22
E=v2+(23kM)x2=constant
Comparing with v2+ω2x2=constant
So, ω=√2k3M⇒T=2π√3M2k
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning
6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective
21 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
A block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View Solution
A uniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force F is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder is
View SolutionA solid cylinder of mass M and radius R pure rolls on a rough surface as shown in the figure. Choose the correct alternative (s).

View SolutionA cylinder of mass m and radius R is kept on a rough surface after giving its centre a horizontal speed v0. Find the speed of the centre of the cylinder when it stops slipping.
View SolutionFind the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.

View SolutionFind the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.

View Solution
A uniform cylinder of mass M and radius R is released from rest on a rough inclined surface of inclination θ with the horizontal as shown in figure. As the cylinder rolls down the inclined surface, the maximum elongation it the spring stiffness k is
View SolutionUniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force is applied at the top point P of the cylinder so that it start pure rolling .In the above question, the frictional force on the cylinder is
View SolutionA solid uniform cylinder of mass M attached to a massless spring of force constant k is placed on a horizontal surface in such a way that cylinder can roll without slipping. If system is released from the stretched position of the spring, then the period will be-
_E01_059_Q01.png)
View SolutionA solid cylinder of mass m length L and radius R is suspended by means of two ropes of length l each as shown. Find the time period of small angular oscillations of the cylinder about its axis AA'
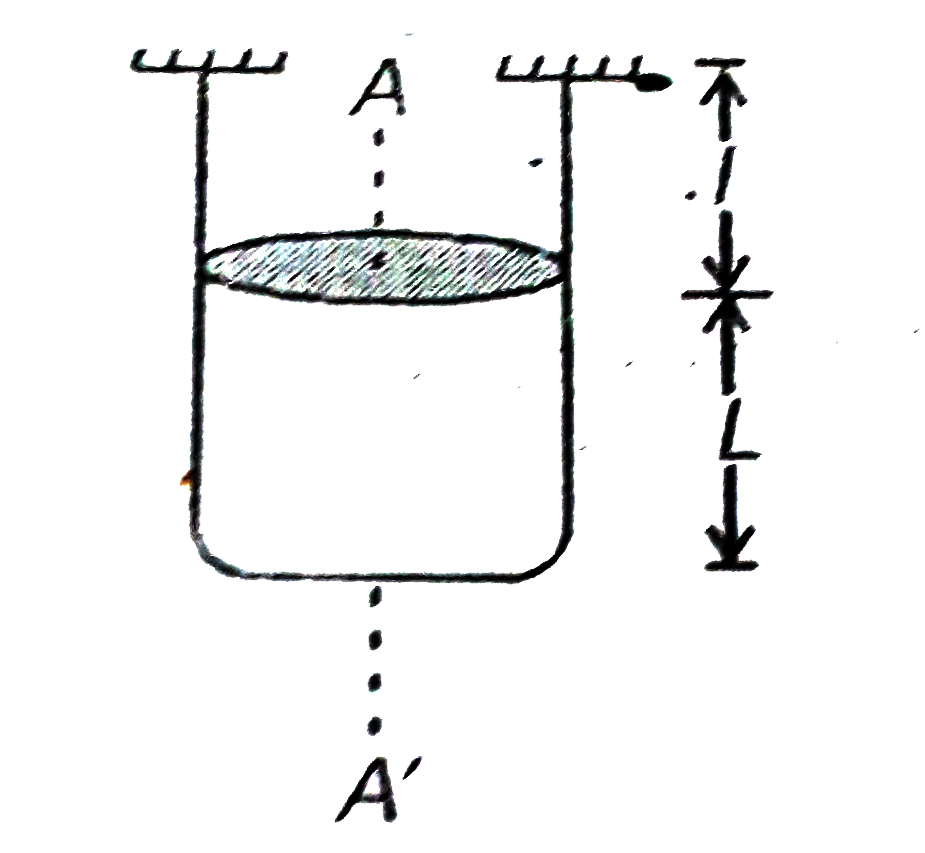
View Solution
