A solenoid is of length 50 cm and has a radius of 2cm. It has 500 turns. Around its central section a coil of 50 turns is wound. Calculate the mutual inductance of the system.
To calculate the mutual inductance of a solenoid with a coil wound around it, we can follow these steps:
Step 1: Identify Given Values
- Length of the solenoid (L) = 50 cm = 0.5 m
- Radius of the solenoid (R) = 2 cm = 0.02 m
- Number of turns in the solenoid (N₁) = 500 turns
- Number of turns in the coil (N₂) = 50 turns
Step 2: Calculate the Number of Turns per Unit Length of the Solenoid
The number of turns per unit length (N₁') of the solenoid can be calculated using the formula:
N₁′=N₁L
Substituting the values:
N₁′=5000.5=1000 turns/m
Step 3: Calculate the Magnetic Field (B) Inside the Solenoid
The magnetic field inside a solenoid is given by:
B=μ0⋅N₁′⋅I
Where μ0 (the permeability of free space) is approximately 4π×10−7T m/A. Thus:
B=4π×10−7⋅1000⋅I=4π×10−4⋅IT
Step 4: Calculate the Area of the Coil
The area (A) of the coil can be calculated using the formula for the area of a circle:
A=πR2
Substituting the radius:
A=π⋅(0.02)2=π⋅0.0004=0.0004πm2
Step 5: Calculate the Magnetic Flux (Φ) Linked with the Coil
The magnetic flux linked with the coil is given by:
Φ=B⋅A
Substituting the expressions for B and A:
Φ=(4π×10−4⋅I)⋅(0.0004π)=1.6π2×10−7IWb
Step 6: Relate Magnetic Flux to Mutual Inductance (M)
The magnetic flux can also be expressed in terms of mutual inductance:
Φ=M⋅I
Equating the two expressions for flux:
M⋅I=1.6π2×10−7I
Thus, we can solve for mutual inductance (M):
M=1.6π2×10−7H
Step 7: Calculate the Total Mutual Inductance for the Coil
Since the coil has 50 turns, the total mutual inductance (M_total) is:
Mtotal=N₂⋅M=50⋅(1.6π2×10−7)
Calculating this gives:
Mtotal=80π2×10−7H≈7.87×10−6H or 78.98μH
Final Answer
The mutual inductance of the system is approximately:
M≈78.98μH
---
- Length of the solenoid (L) = 50 cm = 0.5 m
- Radius of the solenoid (R) = 2 cm = 0.02 m
- Number of turns in the solenoid (N₁) = 500 turns
- Number of turns in the coil (N₂) = 50 turns
The number of turns per unit length (N₁') of the solenoid can be calculated using the formula:
N₁′=N₁L
Substituting the values:
N₁′=5000.5=1000 turns/m
The magnetic field inside a solenoid is given by:
B=μ0⋅N₁′⋅I
Where μ0 (the permeability of free space) is approximately 4π×10−7T m/A. Thus:
B=4π×10−7⋅1000⋅I=4π×10−4⋅IT
The area (A) of the coil can be calculated using the formula for the area of a circle:
A=πR2
Substituting the radius:
A=π⋅(0.02)2=π⋅0.0004=0.0004πm2
The magnetic flux linked with the coil is given by:
Φ=B⋅A
Substituting the expressions for B and A:
Φ=(4π×10−4⋅I)⋅(0.0004π)=1.6π2×10−7IWb
The magnetic flux can also be expressed in terms of mutual inductance:
Φ=M⋅I
Equating the two expressions for flux:
M⋅I=1.6π2×10−7I
Thus, we can solve for mutual inductance (M):
M=1.6π2×10−7H
Since the coil has 50 turns, the total mutual inductance (M_total) is:
Mtotal=N₂⋅M=50⋅(1.6π2×10−7)
Calculating this gives:
Mtotal=80π2×10−7H≈7.87×10−6H or 78.98μH
The mutual inductance of the system is approximately:
M≈78.98μH
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-IA58videos
ELECTROMAGNETIC INDUCTION
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-IB18videos
ELECTROMAGNETIC INDUCTION
- BOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)26videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II22videos
ELECTROMAGNETIC WAVES
Similar Questions
An air cored solenoid is of length 0.3 m, area of cross section 1.2×10−3m2 and has 2500 turns. Around its central section, a coil of 350 turns is wound. The solenoid and the coil are electrically insulated from eachother. Calculate the e.m.f. induced in the coil if the initial current of 3 A in the solenoid is reversed in 0.25 s.
View SolutionOver a solenoid of 50cm length and 2cm radius and having 500turns is would another wire of 50 turns near the centre. Calculate
(i) mutual inductance of the two coils
(ii) Induced emf in the second coil when the current in the primary changes from 0 to 5A in 0.02 sec.View Solution
Knowledge Check
- Question 1 - Select One
If the number of turns per units length of a coils of solenoid is doubled , the self- inductance of the soleniod will
Aremain unchangedBbe halvedCbe doubledDbecome four times - Question 2 - Select One
A 2 m long solenoil with diameter 2 cm and 2000 turns has a secondary coil of 1000 turns wound closely near its midpoint. The mutuat inductance between the two coils is.
A2.4×10−4HB3.9×10−4HC1.28×10−3HD3.14×10−3H
A long solenoid of length L, cross section A having N1 turns has about its center a small coil of N2 turns as shows in Fig The mutual inductance of two circuits is
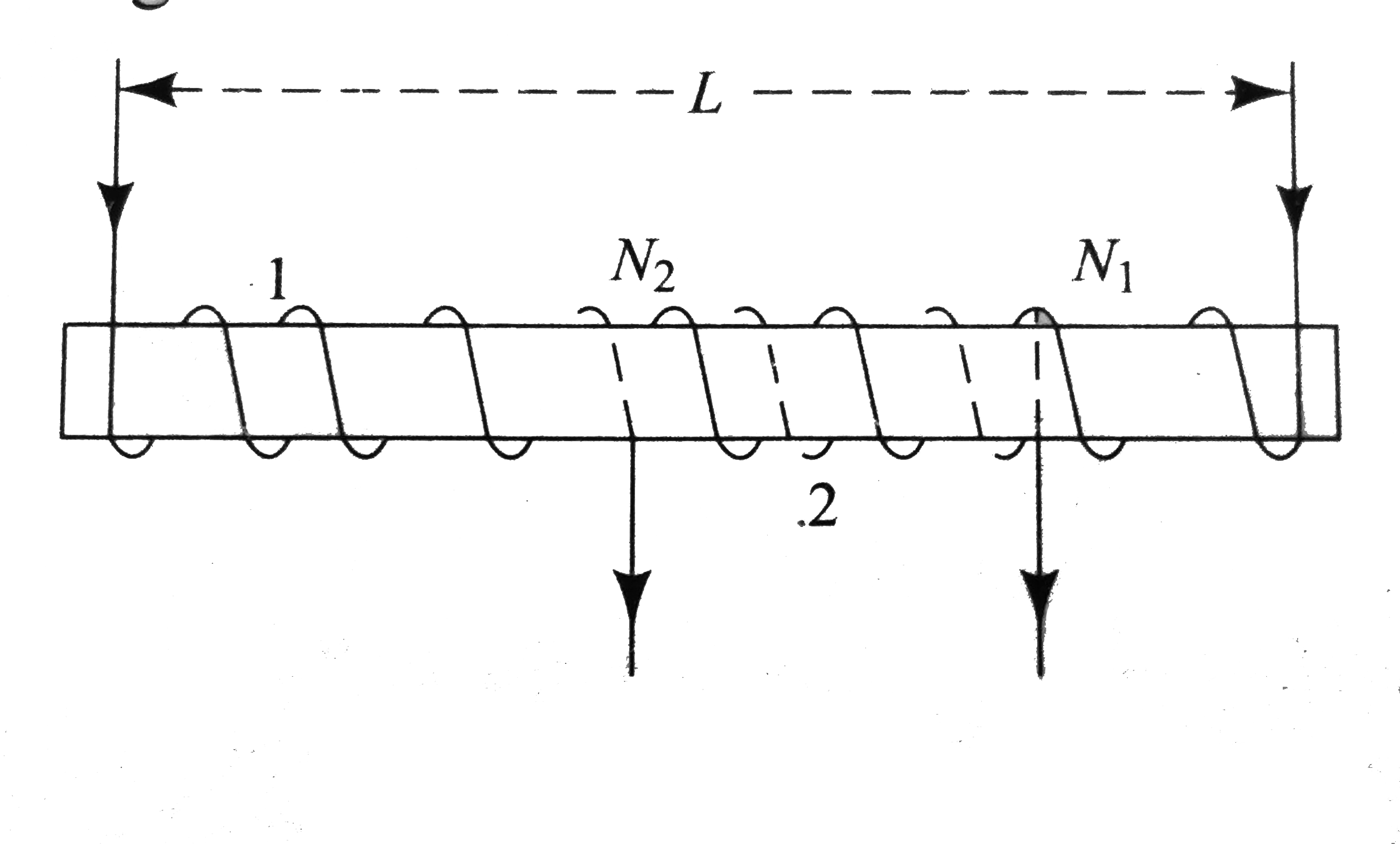 View Solution
View SolutionA solenoid of length 0⋅5m has a radius of 1cm and is made up of 500 turns. It carries a current of 5A. What is the magnitude of the magnetic field inside the solenoid?
View SolutionA solenoid of 2000 turns is wound over a length of 0.3 m. The area aof cross section is 1.3×10−3m2. Around its central seciton, a coil of 300 turns is closely wound. If an initial current of 2 A is reversed in 0.25 s, find the e.m.f induced in the coil .
View SolutionA straight solenoid has 50 turns per cm in primary and total 200 turns in the secondary. The area of cross section of the solenoids is 4cm2. Calculate the mutual inductance. Primary is tightly kept in side the secondary.
View SolutionA solenoid of length 50cm with 20 turns per centimetre and area of cross-section 40cm? completely surrounds another coaxial solenoid of the same length, area of cross-section 25cm2 with 25 turns per centimetre. Calculate the mutual inductance of the system.
View SolutionAn air cored solenoid of length 50 cm and area of cross section 28m2 has 200 turns and carries a current of 5.0 A. On switching off, the current decreases to across the ends of the solenoid. Find flux and emf induced if time is equal to 1.0 ms.
View Solution

