A solid cube of wood of side 2a and mass M is resting on a horizontal surface. The cube is constrained to rotate about an axis passing through D and perpendicular to face ABCD. A bullet of mass m and speed v is shot at a height of 4a/3 as shown in the figure. The bullet becomes embedded in the cube. Find the minimum value of v required to topple the cube. Assume m>>M.

Let ω be the angular velocity of cube just after collison about an axis passing through D. From conservation of the angular mometum about an axis passing through D.

mv(4a3)=ID.ω
Here ID=Icom+mr2
where r= perpedicular distance of axis of rotation passing through D from centre of mass (com) of the cube =√2a
or 4mva3=[M(42+4a212)+M(2a2)]ω
or 4mva3=83Ma2.ω
ω=12mvMa........i
The cube will topple if its COM is just able to reach in a vertical height h2 as shown in figure.

Hence applying conservation of mechanical energy
12IDω2=Mg(h2−h1) (∵ID=83Ma2)
or 12(83Ma2).{12mvMa}2=Mg(√2−1a
or 12(mM)2v2=ag(√2−1)
or v=Mm[3ag(√2−1)]12
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Solved Examples12videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.111videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A bullet of mass m strikes a block of mass M. The bullet remains embedded in the block. Find the amplitude of the resulting SHM.
 View Solution
View SolutionIn the figure shown ABCD is a lamina of mass 12kg. The moment of inertia of the given body about an axis passing through D, and perpendicular to the plane of the body is
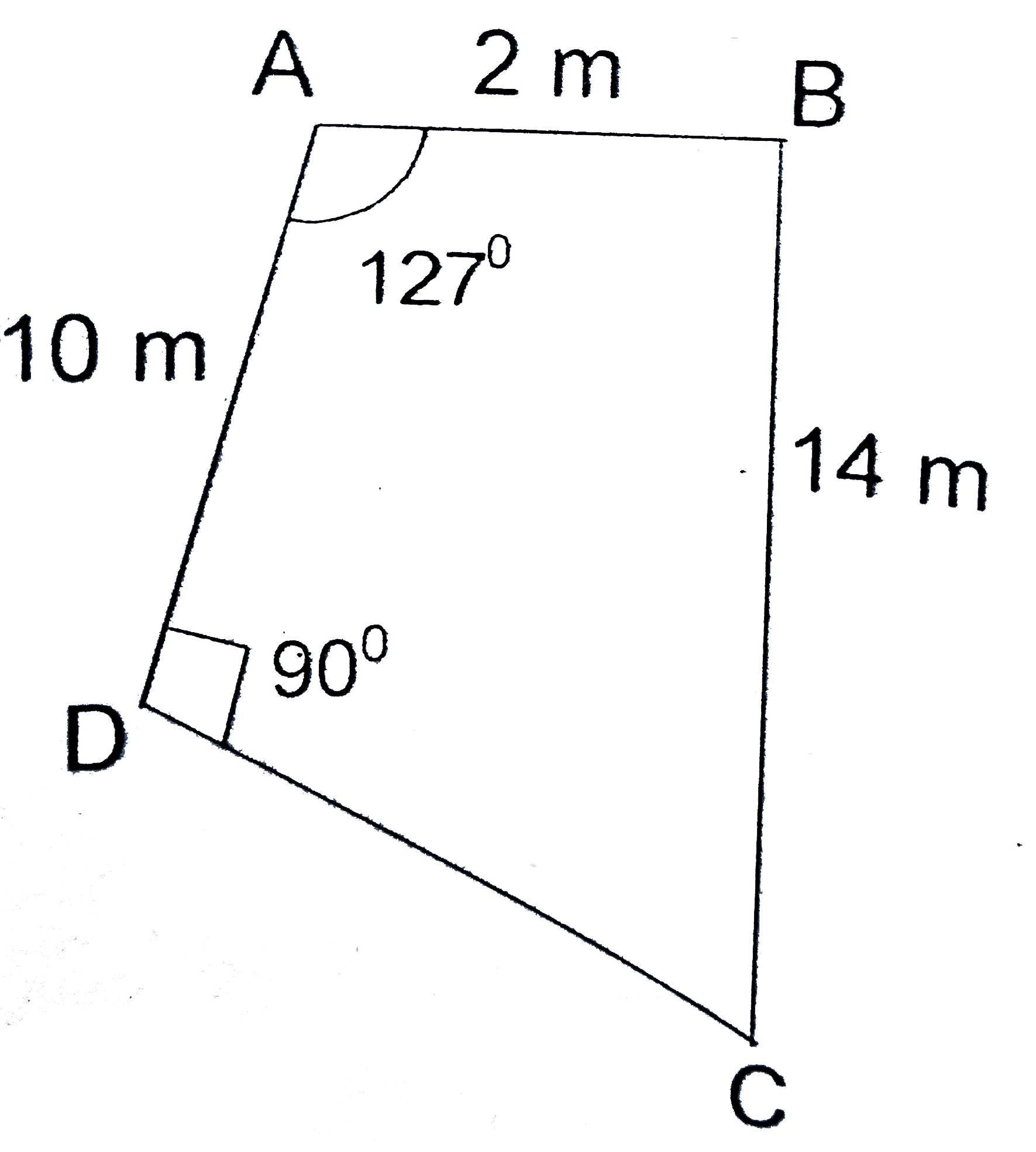 View Solution
View SolutionFrom a solid sphere of M and radius R a cube of maximum possible volume is cut. Moment of inertia of cube about an axis passing through its centre and perpendiular to one of its faces is:
View SolutionFigure shows a cubical wooden block of side length a and mass M which is resting over a horizontal surface and constrained to rotate about its right lower edge D. A bullet of mass m moving horizontally, directly towards its centre with velocity v strikes and gets embedded in it. During subsequent motion the block just topples, calculate v. Assume m<<M.
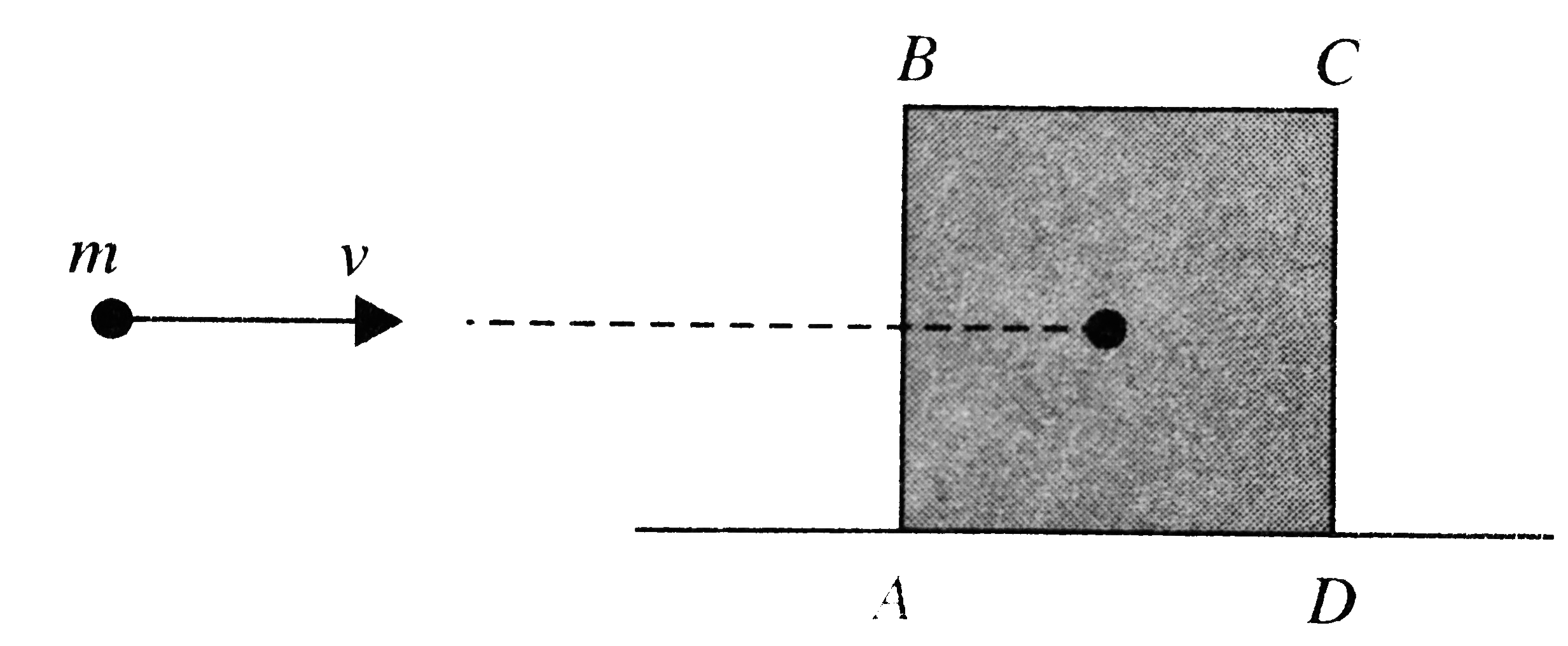 View Solution
View SolutionThe moment of inertia of a cube of mass M and edge length a about an axis passing through one of its edge is
View SolutionA disc of mass m and radius R is kept on a smooth horizontal surface with its plane parallel to the surface. A particle of same mass m travelling with speed v0 collides with the stationery disc and gets embedded into it as shown in the figure. Then
 View Solution
View SolutionA square of a side a is cut from a square of side 2a as shown in the figure. Mass of this square with a hole is M. Then its moment of inertia about an axis passing through its centre of mass and perpendicular to its plane will be
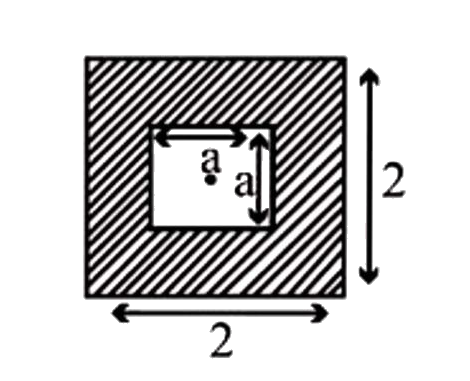 View Solution
View SolutionA cube of mass m and side a is moving along a plane with constant speed vo as shown in figure. The magnitude of angular momentum of the cube about z -axis would be.
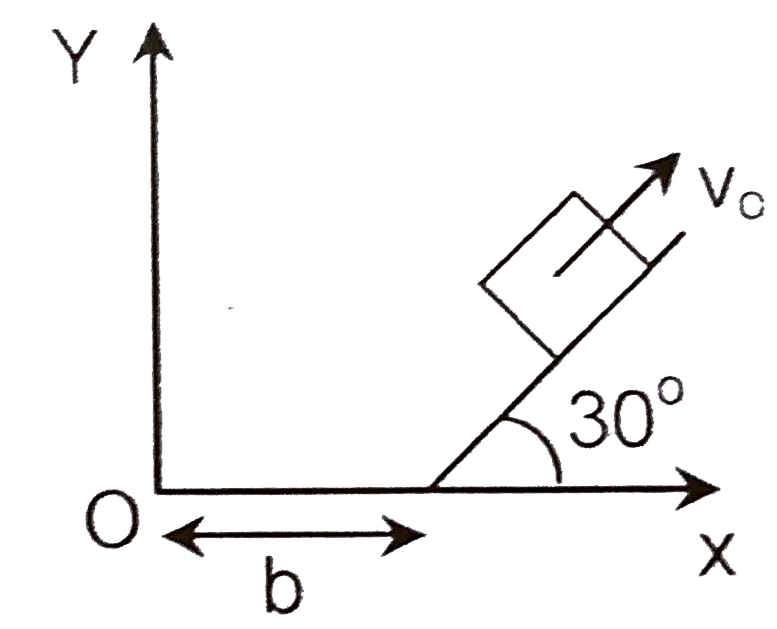 View Solution
View SolutionA block of mass m is placed at the top of a smooth wedge ABC. The wedge is rotated about an axis passing through C as shown in the figure - 3.81. The minimum value of angular speed ω such that the block does not slip on the wedge is :
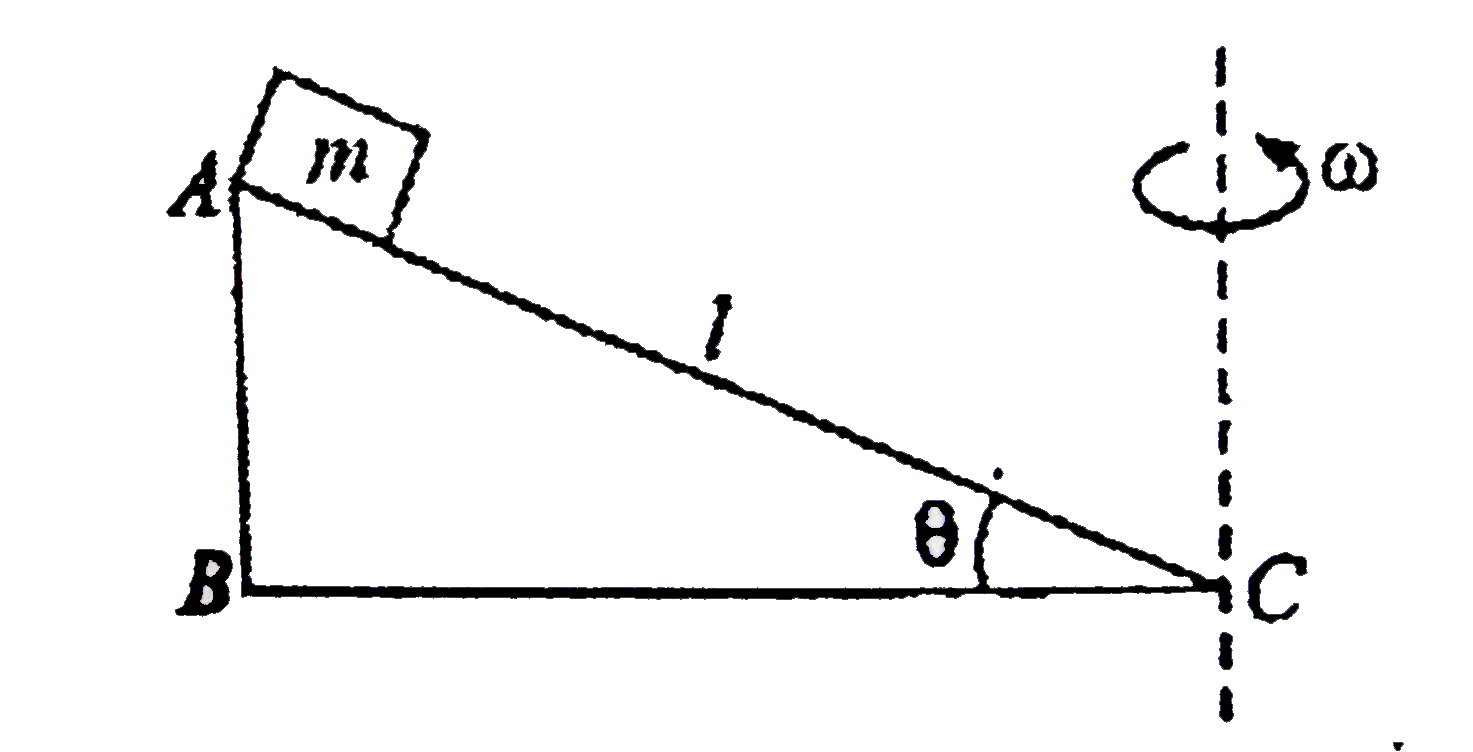 View Solution
View Solution
A uniform rod of mass m is rotated about an axis passing through point O as shown. Find angular momentum of the rod about rotational law.View Solution
