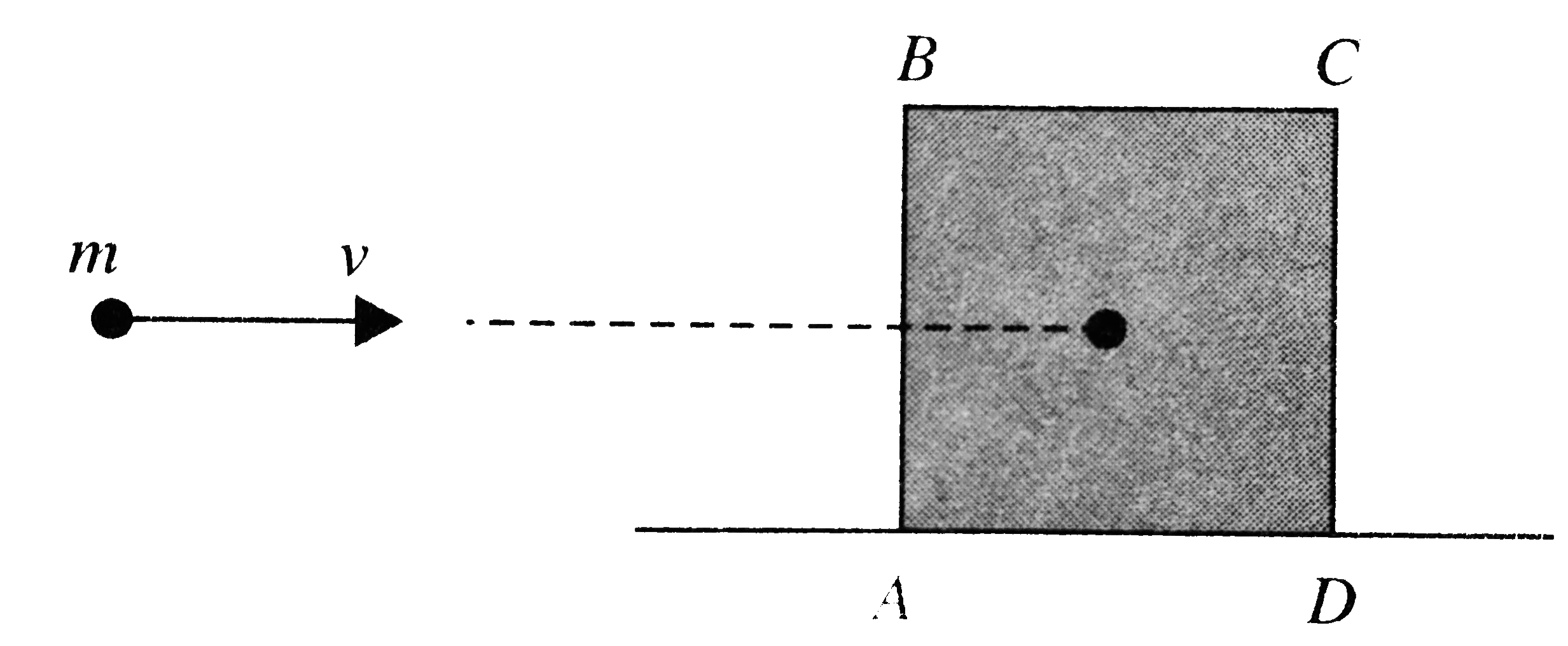
Figure shows a cubical wooden block of side length a and mass which is resting over a horizontal surface and constrained to rotate about its right lower edge . A bullet of mass m moving horizontally, directly towards its centre with velocity strikes and gets embedded in it. During subsequent motion the block just topples, calculate . Assume .
The correct Answer is:
Moment of inertia of block about its edge is equal to
When bullet strikes the blocks and gets embedded into it even then moment of inertia remains practically equla to because
During the collision, a reaction is offered by . Hence momentum of the system dies not remain constant but the angular momentum of the sytem remains constant about because angular impulse produced by the reaction is zero about itself.
If angular velocity of the block, just after the collision is then according to law of coservation of angular momentum,
The block will jus topple, if the block reaches to the positioin shown in figure
Here of the system

Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Single Correct142videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct26videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.413videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A solid cube of wood of side 2a and mass M is resting on a horizontal surface. The cube is constrained to rotate about an axis passing through D and perpendicular to face ABCD. A bullet of mass m and speed v is shot at a height of 4a/3 as shown in the figure. The bullet becomes embedded in the cube. Find the minimum value of v required to topple the cube. Assume m>>M.
 View Solution
View SolutionA bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
View Solution
Knowledge Check
- Question 1 - Select One
A bullet of mass m moving horizontally with a velocity v strikes a block of wood of mass M and gets embedded in the block. The block is suspended from the ceiling by a massless string. The height to which block rises is
Av22g(mM+m)2Bv22g(M+mm)2Cv22g(mM)2Dv22g(Mm)2
Two identical blocks A and B of mass M each are kept on each other on a smooth horizontal plane. There exists friction between A and B. A bullet of mass m hits the the lower block with a horizontal velocity v and goes embedded into it. Find the work done by friction between A and B.
View SolutionA disc of mass m and radius R is kept on a smooth horizontal surface with its plane parallel to the surface. A particle of same mass m travelling with speed v0 collides with the stationery disc and gets embedded into it as shown in the figure. Then
 View Solution
View SolutionA uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
View SolutionA uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
View SolutionTwo blocks of masses m and 3m are connected by an inextensible string and the string passes over a fixed pulley which is massless and frictionless. A bullet of mass m moving with a velocity 'u' hits the hanging block of mass 'm' and gets exbedded in it. Find the height through which block A rises after the collision.
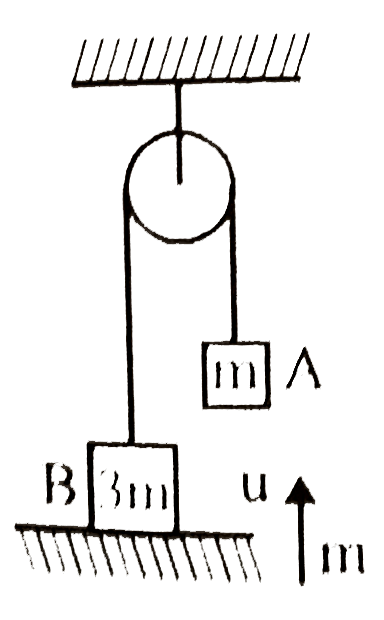 View Solution
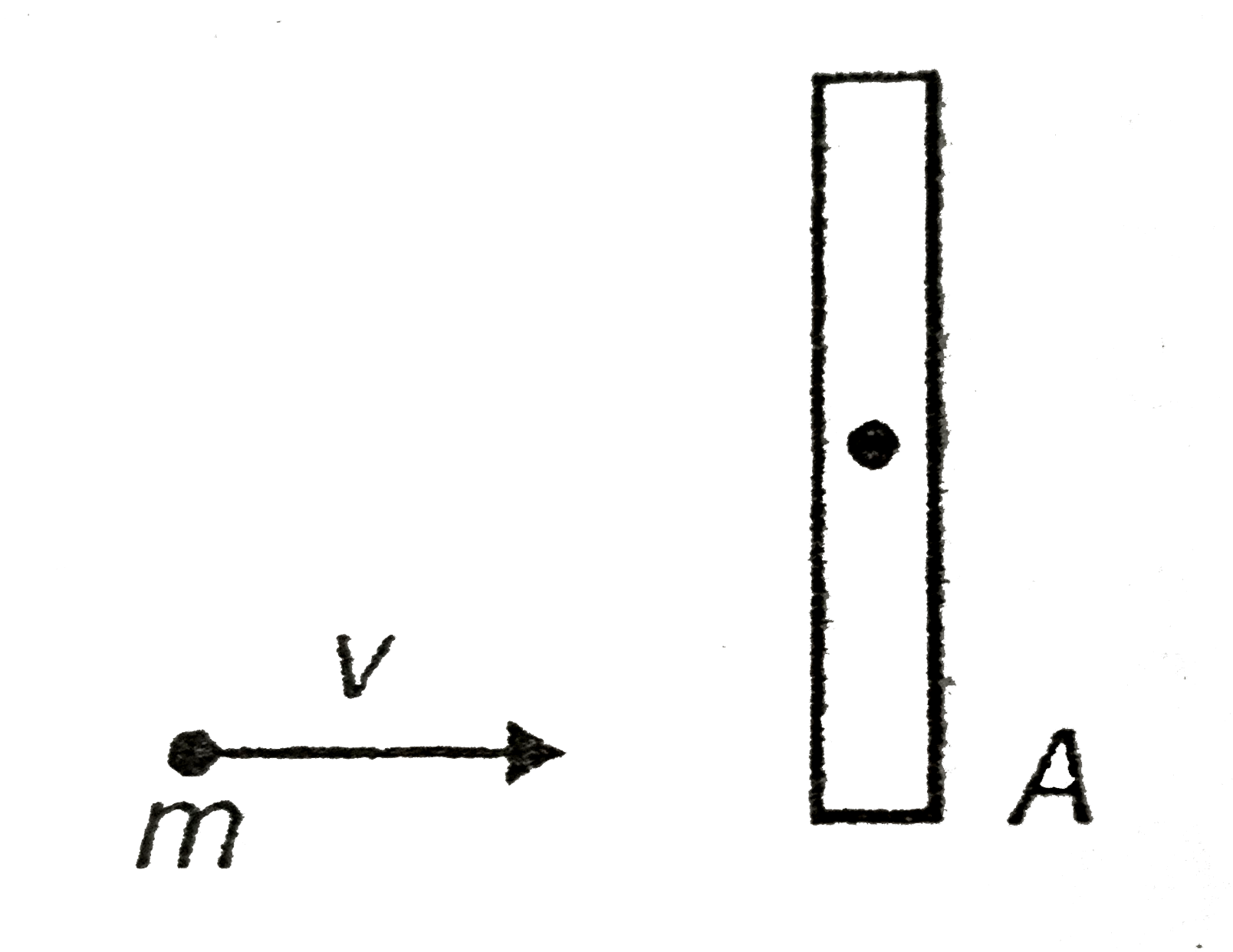
View SolutionA rod of mass m and length l hinged at the centre is placed on a horizontal surface. A bullet of mass m moving with velocity v strikes the end A of the rod and gets embedded in it. The angular velocity with which the systems rotates about its centre of mass after the bullet strikes the rod
 View Solution
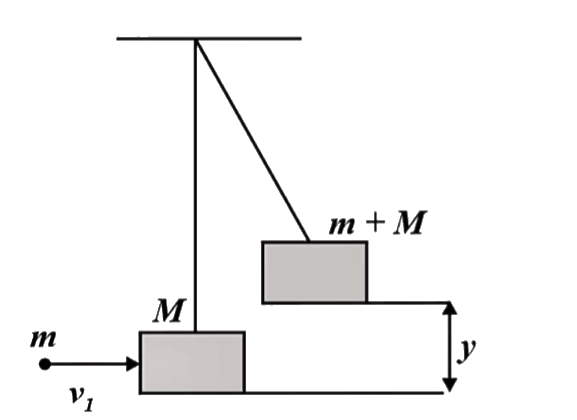
View SolutionA bullet of mass m moving with velocity υ1 strikes a suspended wooden block of mass M as shown in the figure and sticks to it. If the block rises to a height y. the initial of the bullet is
 View Solution
View Solution

