A solid cylinder of mass M=10kg and cross - sectional area A=20cm2 is suspended by a spring of force contant k=100N/m and hangs partically immersed in water. Calculate the period of small oscillation of the cylinder.
The correct Answer is:A
In such situation, upthrust also behaves like a spring force of force constant =ρAg

K≠t in the given situation is (k+ρAg)
∴T=2π√mk+ρAg
=2π√10100+1000×20×10−4×10
=1.8s
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 Single Correct
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 More Than One Correct
8 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Single Correct
24 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
A uniform cylinder of height h, mass m and cross sectional area A is suspended vertically from a fixed point by a massless spring of force constant k, A beaker full of water is placed under the cylinder so that 1/4th of its volume is submerged in the water at equilibrium position. When the cylinder is given a small downward push and released, it starts oscillating vertically with small amplitude. Calculate the frequency of oscillation of the cylinder, Take, density of water =ρ.
View SolutionA solid cylinder of mass m length L and radius R is suspended by means of two ropes of length l each as shown. Find the time period of small angular oscillations of the cylinder about its axis AA'
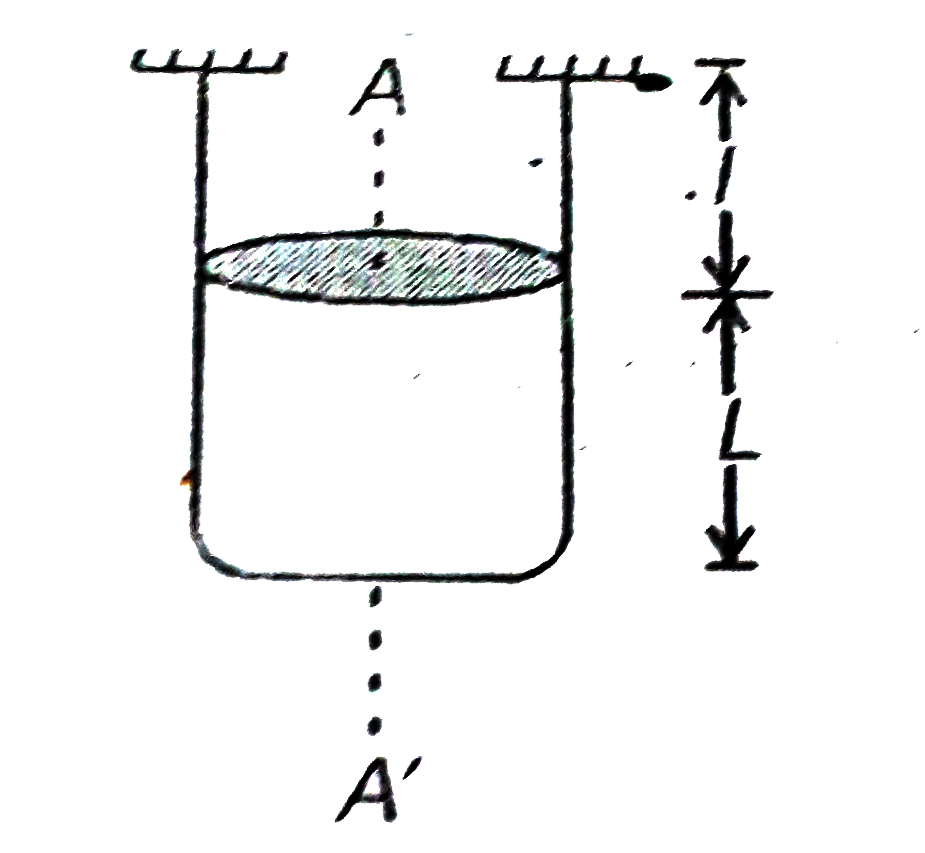
View Solution
Knowledge Check
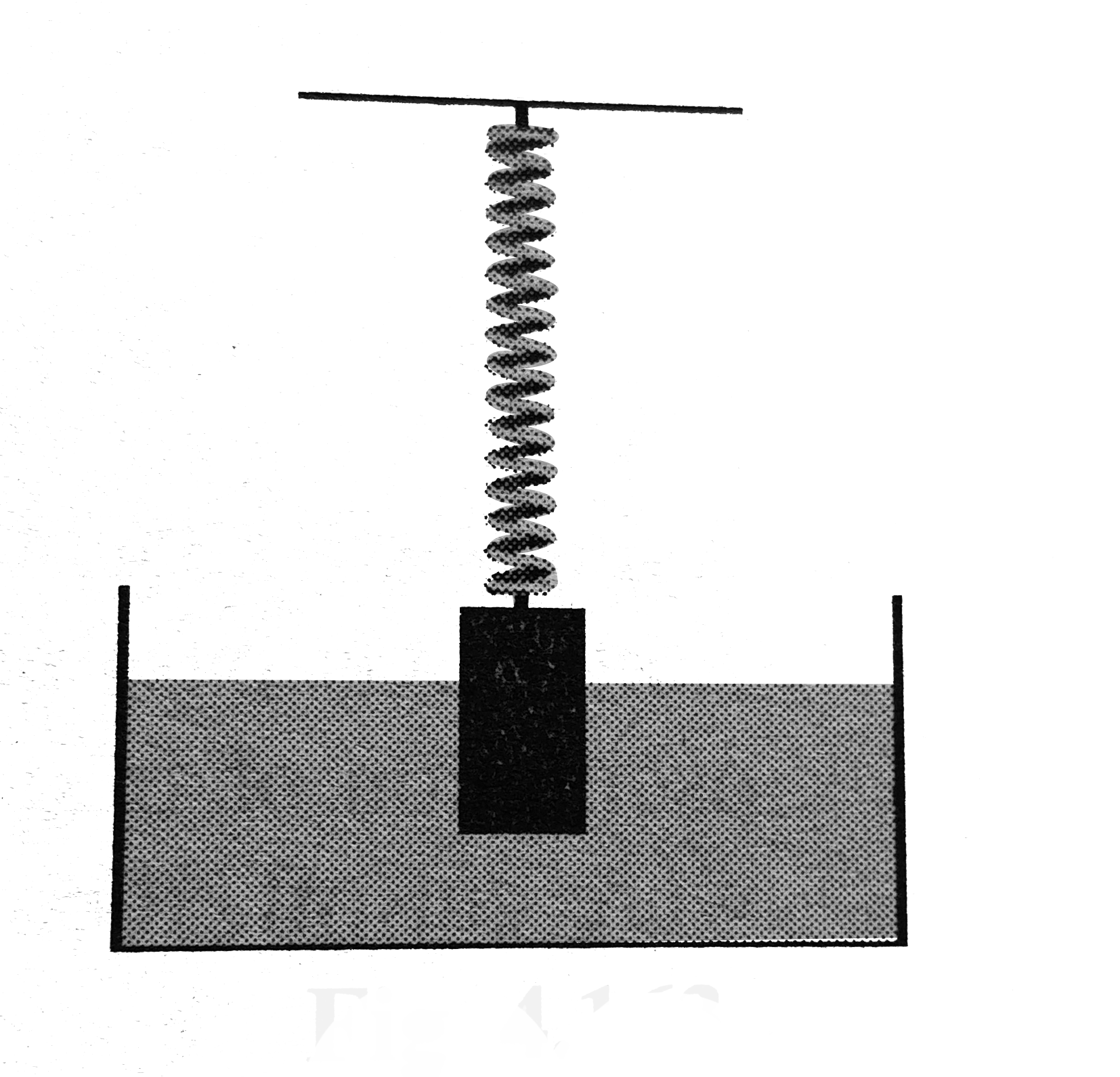
A solid right circular cylinder of weight 10 kg and cross sectional area 100cm2 is suspended by a spring, where k=1kgcm, and hangs partially submerged in water of density 1000kgm3 as shown in Fig. What is its perod when it makes simple harmonic vertical oscillations? (Take g=10ms2)A0.6 sB1 sC1.5 sD2.2 s
A mass m is suspended from a spring of force constant k and just touches another identical spring fixed to the floor as shown in the fig. The time period of small oscillations isA2π√mkBπ√mk+π√mk2Cπ√m3k2Dπ√mk+π√m2kA mass m is suspended from a spring of force constant k and just touches another idential spring fixed to the floras shown in the figure. The time period of small oscillation is
 A2π√mkBπ√mk+π√mk/2Cπ√m3k/2Dπ√mk+π√m2k
A2π√mkBπ√mk+π√mk/2Cπ√m3k/2Dπ√mk+π√m2k
The period of oscillation of a mass M, hanging from a spring of force constant k is T. When additional mass m is attached to the spring, the period of oscillation becomes 5T/4. m/M =
View SolutionA uniform cylinder of mass m, length l and cross sectional area A is suspended with its vertical from a fixed point, with the help of a massless spirng of force constant (K), The cylinder is then submerged in a liquid of density p. At equilibrium the cylinder remains submerged in the liquid with 1/4th of its volume outside the liquid, as shown in the figure. The elongation of hte spring at this point is x0. WHen the cylinder is given a slight downward push into the liquid and then released, its starts oscillating with vertical S.H.M. of small amplitude.

Time period of vertical S.H.M of the cylinder is
View SolutionA uniform cylinder of length L and mass M having cross-sectional area A is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half submerged in a liquid of density σ at equilibrium position. When the cylinder is given a downward push and released, it starts oscillating vertically with a small amplitude. The time period T of the oscillations of the cylinder will be :
View SolutionA uniform cylinder of mass m, length l and cross sectional area A is suspended with its vertical from a fixed point, with the help of a massless spirng of force constant (K), The cylinder is then submerged in a liquid of density p. At equilibrium the cylinder remains submerged in the liquid with 1/4th of its volume outside the liquid, as shown in the figure. The elongation of hte spring at this point is x0. WHen the cylinder is given a slight downward push into the liquid and then released, its starts oscillating with vertical S.H.M. of small amplitude.

If the cyleinder is displced by a small downward displacement a from its equilibrium postion and then released , the restoring force on it will be
View SolutionA uniform cylinder of mass m, length l and cross sectional area A is suspended with its vertical from a fixed point, with the help of a massless spirng of force constant (K), The cylinder is then submerged in a liquid of density p. At equilibrium the cylinder remains submerged in the liquid with 1/4th of its volume outside the liquid, as shown in the figure. The elongation of hte spring at this point is x0. WHen the cylinder is given a slight downward push into the liquid and then released, its starts oscillating with vertical S.H.M. of small amplitude.

The elongation X0 produced in the springs when the syste is in equilibrium is
View Solution
