A solid cylinder of mass M=10kg and cross - sectional area A=20cm2 is suspended by a spring of force contant k=100N/m and hangs partically immersed in water. Calculate the period of small oscillation of the cylinder.
The correct Answer is:A
To calculate the period of small oscillation of a solid cylinder partially immersed in water, we will follow these steps:
Step 1: Identify the given values
- Mass of the cylinder, M=10kg
- Cross-sectional area, A=20cm2=20×10−4m2=0.002m2
- Spring constant, k=100N/m
- Density of water, ρ=1000kg/m3
- Acceleration due to gravity, g=10m/s2
Step 2: Calculate the upthrust (buoyant force)
The upthrust Fb can be calculated using the formula:
Fb=ρ⋅A⋅g
Substituting the values:
Fb=1000kg/m3⋅0.002m2⋅10m/s2=20N
Step 3: Calculate the effective spring constant
The effective spring constant knet is the sum of the spring constant k and the equivalent spring constant due to the buoyant force:
knet=k+Fb
Substituting the values:
knet=100N/m+20N=120N/m
Step 4: Calculate the period of oscillation
The period T of small oscillations is given by the formula:
T=2π√Mknet
Substituting the values:
T=2π√10kg120N/m
Calculating the value:
T=2π√10120=2π√112≈2π⋅0.2887≈1.81s
Conclusion
The period of small oscillation of the cylinder is approximately T≈1.81s.
---
- Mass of the cylinder, M=10kg
- Cross-sectional area, A=20cm2=20×10−4m2=0.002m2
- Spring constant, k=100N/m
- Density of water, ρ=1000kg/m3
- Acceleration due to gravity, g=10m/s2
The upthrust Fb can be calculated using the formula:
Fb=ρ⋅A⋅g
Substituting the values:
Fb=1000kg/m3⋅0.002m2⋅10m/s2=20N
The effective spring constant knet is the sum of the spring constant k and the equivalent spring constant due to the buoyant force:
knet=k+Fb
Substituting the values:
knet=100N/m+20N=120N/m
The period T of small oscillations is given by the formula:
T=2π√Mknet
Substituting the values:
T=2π√10kg120N/m
Calculating the value:
T=2π√10120=2π√112≈2π⋅0.2887≈1.81s
The period of small oscillation of the cylinder is approximately T≈1.81s.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 Single Correct
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 More Than One Correct
8 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Single Correct
24 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
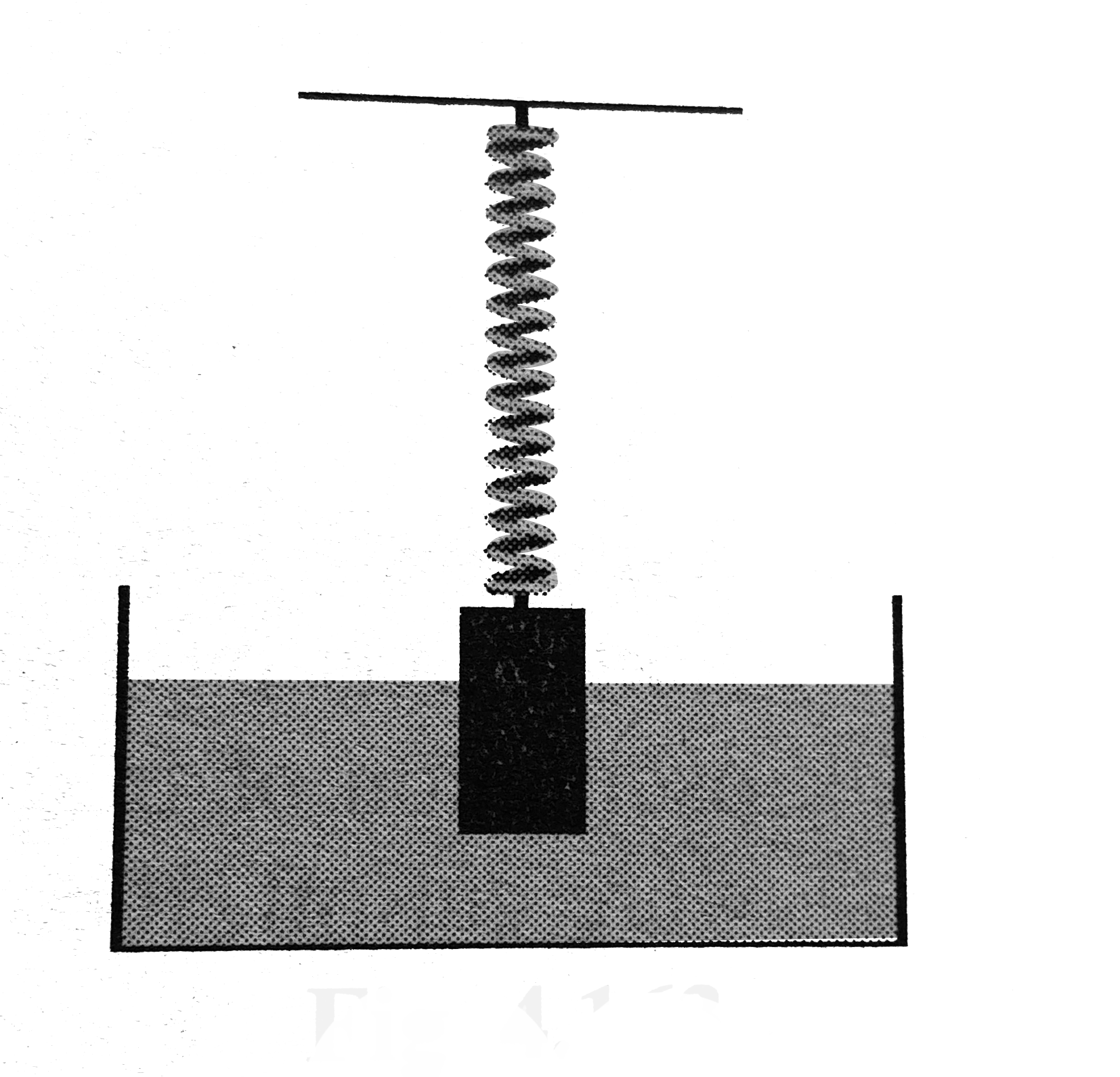
A solid right circular cylinder of weight 10 kg and cross sectional area 100cm2 is suspended by a spring, where k=1kgcm, and hangs partially submerged in water of density 1000kgm3 as shown in Fig. What is its perod when it makes simple harmonic vertical oscillations? (Take g=10ms2)
View Solution
A mass m is suspended from a spring of force constant k and just touches another identical spring fixed to the floor as shown in the fig. The time period of small oscillations is
View SolutionA spring of force constant 'k' is cut into four equal parts one part is attached with a mass m. The time period of oscillation will be
View SolutionA solid sphere of mass m is attached to a light spring of force constant k so that it can roll without slipping along a horizontal surface. Calculate the period of oscillation made by sphere.

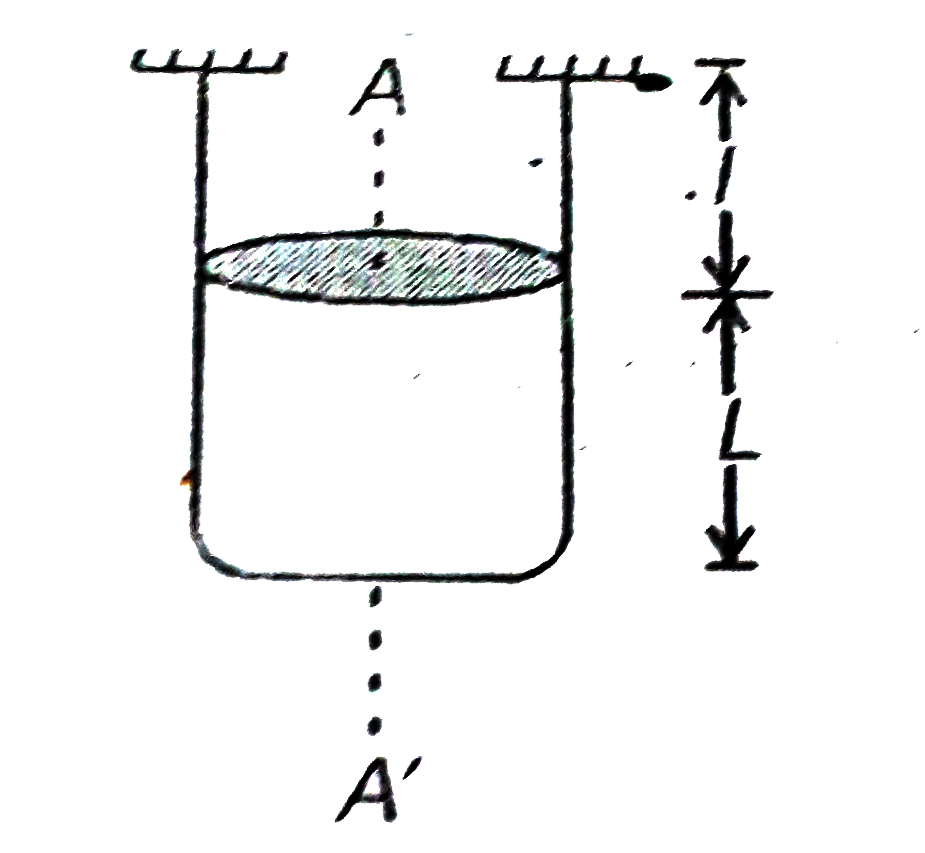
View SolutionA solid cylinder of mass m length L and radius R is suspended by means of two ropes of length l each as shown. Find the time period of small angular oscillations of the cylinder about its axis AA'
View Solutionfigure shown a partical mass m=100g attaches with four identical spring , each of length l=10cm . Initial tension in each spring is F0=25N. Neglecting gravity , Calculate the period of small oscillation of the article along a line perpendicular to the plane of the figure .

View SolutionFigure shows a particle mass m=100g attaches with four identical spring , each of length l=10cm . Initial tension in each spring is F0=25N. Neglecting gravity , Calculate the period of small oscillation of the particle along a line perpendicular to the plane of the figure .

View SolutionA cylindrical object of cork of mass 15g and cross-sectional area A1=10cm2 floats in a pan of water as shown in the figure. An aluminum, cylinder of mass 25g and cross-sectional area A2=2cm2 is attached 4cm below the cork and slides through a watertight frictionless hole in the bottom of the pan. Take density of the cork, ρ=0.2g/cm3,ρaluminium=2.7g/cm3,g=10m/s2. Based on the above information, answer the following questions.

The length of the cork cylinder inside the water in equilibrium is
View SolutionA block of mass 0.2 kg is attached to a mass less spring of force constant 80 N/m as shown in figure. Find the period of oscillation. Take g=10m/s2. Neglect friction

View SolutionA block of mass 0.2 kg is attached to a mass less spring of force constant 80 N/m as shown in figure. Find the period of oscillation. Take g=10m/s2. Neglect friction

View Solution
