A solid cylinder of mass $M$ and radius $R$ rolls without slipping down an inclined plane of length $L$ and height $h$ . What is the speed of its center of mass when the cylinder reaches its bottom

Video Solution

Text Solution

Verified by Experts

First method: "Force/Torque" Method
We can use the formula which we derived
$a = \frac{g sin θ}{1 + \frac{k^{2}}{R^{2}}}$ ……..i
For cylinder $I = \frac{m R^{2}}{2} \Rightarrow k^{2} = \frac{R^{2}}{2}$
Hence, acceleration of the cylinder $a = \frac{2}{3} g sin θ$
Let $v_{C M}$ be the velocity of the centre of mas at the bottom. From equation $v^{2} = u^{2} + 2 a s$ ,
$v_{C M}^{2} = 0^{2} + 2 (\frac{2}{3} g sin θ) (\frac{h}{sin θ}) = \frac{4}{3} g h$
$\Rightarrow v_{C M} = \sqrt{\frac{4}{3} g h}$
Second method: By Mechanical Energy Conservation
When the non conservative forces do not perform ay work on a system $(W_{nef} = 0)$ , the mechanical energy $(K + U)$ of the system remains constant.
Here $W_{f} = 0$ (because the velocity of the instantaneous point of contact is always zero)
$W_{N} = 0$ (because the velocity of the instantaneous point of contact is always zero)
Thus, $W_{nef} = 0$
The mechanical energy of the cylinder will remain constant.
${(K + U)}_{top} = {(K + U)}_{bottom}$
$\Rightarrow 0 + m g h = \frac{1}{2} m v_{C M}^{2} + \frac{1}{2} I_{C M} ω^{2} + 0$
$= \frac{1}{2} m v_{C M}^{2} + \frac{1}{2} (\frac{1}{2} m r^{2}) {(\frac{v_{C M}}{r})}^{2}$
$(v_{C M} = r ω,$ for rolling)
$= \frac{1}{2} m v_{C M}^{2} + \frac{1}{4} m v_{C M}^{2} \Rightarrow m g h = \frac{3}{4} m v_{C M}^{2}$
$\Rightarrow v_{C M} = \sqrt{\frac{4}{3} g h}$
Third Method: Using work energy Theorem $(Σ W = △ K)$
$W_{f} + W_{N} + W_{m g} = K_{2} - K_{1}$
$\Rightarrow 0 + 0 + (m g) h = (\frac{1}{2} m v_{C M}^{2} + \frac{1}{2} I_{C M} ω^{2})$
$\Rightarrow m g h = \frac{1}{2} m v_{C M}^{2} \Rightarrow m g h = \frac{3}{4} m v_{C M}^{2}$
$\Rightarrow v_{C M} = \sqrt{\frac{4}{3} g h}$
Fourth Method: Using work Ennergy Theorem Separately in Translational Motion and Rotational Motion
The rolling motioin of the cylinder is obtained by superimposing the translation and rotational motions, translational motion of the centre of mass and rotational motion about an axis passing through the centre of mass, cylinder's own axis.
you can apply the work energy theorem for the translational and rotatioinal components of the motion separately as under:
$Σ W_{force} = △ K_{translation}$
and. $Σ W_{torque} = (△ K_{rotational})$
The two forces acting at the point of contact, $f_{s}$ and $N$ can be translated to the centre of mass after applying an equivalent torque as shown in figure.
For the translational part of the motion.
$W_{f} + W_{N} + W (m g) = K_{2} - K_{1}$

$\Rightarrow - f_{s} (\frac{h}{sin θ}) + 0 + h = \frac{1}{2} m v + {(C M)}^{1} - 0$
For the rotational part,
Torque $\times$ Angular displacement $= \frac{1}{2} I_{C M} ω^{2} - 0$
$\Rightarrow (f_{s} . r) ⎛ ⎝ \frac{\frac{h}{sin θ}}{r} ⎞ ⎠ = \frac{1}{2} I_{C M} ω^{2} - 0$
$(W τ = τ θ)$ is $τ$ is contant and $θ_{1}$ and $τ$ are in the same sense of rotation where $θ_{1}$ is the angle through which the cyinder rotates about the centre of mass axis. Here, for rolling, $v_{C M} = r ω s, a_{C M} = r α$ and $s = r θ_{1})$
Thus $f_{s} (\frac{h}{sin θ}) = \frac{1}{2} I_{C M} ω^{2}$
From the above equations, we get
$m g h = \frac{1}{2} m v_{C M}^{2} + \frac{1}{2} I_{C M} + ω_{C M}^{2}$
$= \frac{3}{4} m v_{C M}^{2} +, I_{C M} = \frac{1}{2} m r^{2}$
$\Rightarrow v_{C M} = \sqrt{\frac{4}{3} g h}$
Fifth method:

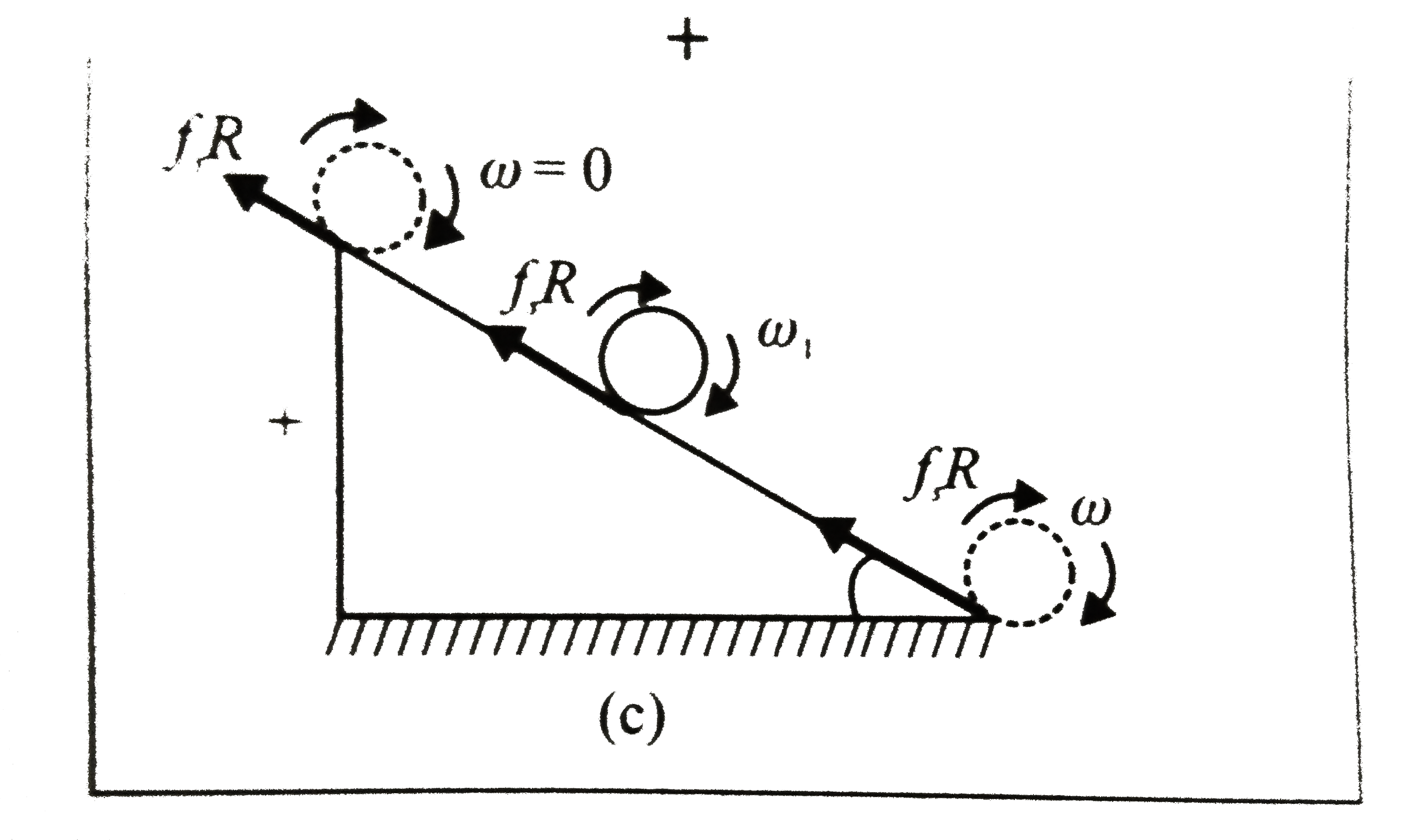
About the instantaneous point of contact, the torque acting on the cylinder is
$(\to τ = f_{s} \times 0 + N) + (m g) (r sin θ)$
$= m g r sin θ (- ˆ k) (c l o c k w i s e)$
Angular momentum of the cylinder about the instantaneous point of contact in the clockwise sense,
$\to L = [I_{C M} ω + m v_{C M} r] (- ˆ k)$
$[(\frac{1}{2} m r^{2}) (\frac{v_{C M}}{r}) + m v_{C M} r] (- ˆ k) = \frac{3}{2} m r v_{C M} (- ˆ k)$
now, from the equation $\to τ = \frac{- \to d L}{d t},$
$m g r sin θ s = \frac{d}{d t} (\frac{3}{2} m r v_{C M})$
Here $\to r τ = \frac{- \to d L}{d t}$ has been applied about the instantaneous point of contact).
$\Rightarrow m g r sin θ \frac{3}{2} m r \frac{d v_{C M}}{d t} = \frac{3}{2} m r a_{C M}$
$\Rightarrow a_{C M} = \frac{3}{2} g sin θ$
Now from the equation $v^{2} = u^{2} + 2 a s,$ we get
$v_{C M}^{2} = 0^{2} + 2 (\frac{2}{3} g sin θ) (\frac{h}{sin θ})$
$\Rightarrow v_{C M} = \sqrt{\frac{4}{3} g h}$
Alternative Method: You can also manipulate Eqn i as follows
$m g r s i θ = \frac{d}{d t} (\frac{3}{2} m r v_{C M})$
$g sin θ = \frac{3}{2} \frac{d v_{C M}}{d t} = \frac{3}{2} \frac{d v_{C M}}{d x} \frac{d x}{d t} = \frac{3}{2} v_{C M} \frac{d v_{C M}}{d x})$
$\Rightarrow g sin θ d x = \frac{3}{2} v_{C M} d v_{C M}$
$\int_{0}^{h / sin θ} g sin θ d x = \int_{0}^{v_{C M}} \frac{3}{2} v_{C M} d v_{C M}$
$\Rightarrow g h = \frac{3}{4} v_{C M}^{2} \Rightarrow v_{C M} = \sqrt{\frac{4}{3} g h}$

Updated on:21/07/2023