A solid cylinder of mass m is attached to a horizontal spring with force constant k. The cylinder can roll without slipping along the horizontal plane. (See the accompanying figure.) Show that the center of mass of the cylinder executes simple harmonic motion with a period T=2π√3m2k, if displaced from mean position.

The correct Answer is:A
In displaced position,
E=12kx2+12mv2+12Iω2
putting I=12mR2
and ω=vR
we get E=12kx2+34mv2
Since, E = constant
∴dEdt=0
or 0=12k(dxdt)(2x)+34m(2v)dvdt
putting, dxdt=v and dvdt=a
we get, F=(ma)=−(2k3)x
Since, F∝−x motion is simple harmonic
ke=−2k3
T=2π√mke=2π√3m2k Hence proved.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 Single Correct28videos
SIMPLE HARMONIC MOTION
- BOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 More Than One Correct8videos
SIMPLE HARMONIC MOTION
- BOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Single Correct24videos
SIMPLE HARMONIC MOTION
- BOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct3videos
SEMICONDUCTORS AND ELECTRONIC DEVICES
- BOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)38videos
SOLVD PAPERS 2017 NEET, AIIMS & JIPMER
Similar Questions
A solid sphere of mass m is attached to a light spring of force constant k so that it can roll without slipping along a horizontal surface. Calculate the period of oscillation made by sphere.
 View Solution
View SolutionA small solid cylinder of mass M attached to horizontal massless spring can roll without slipping along a horizontal surface. Show that if the cylinder is displaced slightly and released, it executes S.H.M. Also find its time period.
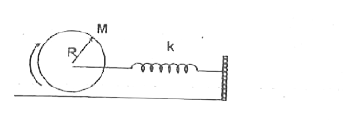 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A disc of mass M is attached to a horizontal massless spring of force constant K so that it can roll with out slipping along a horizontal surface. If the disc is pulled a little towards right and then released, its centre of mass executes SHM with a period of
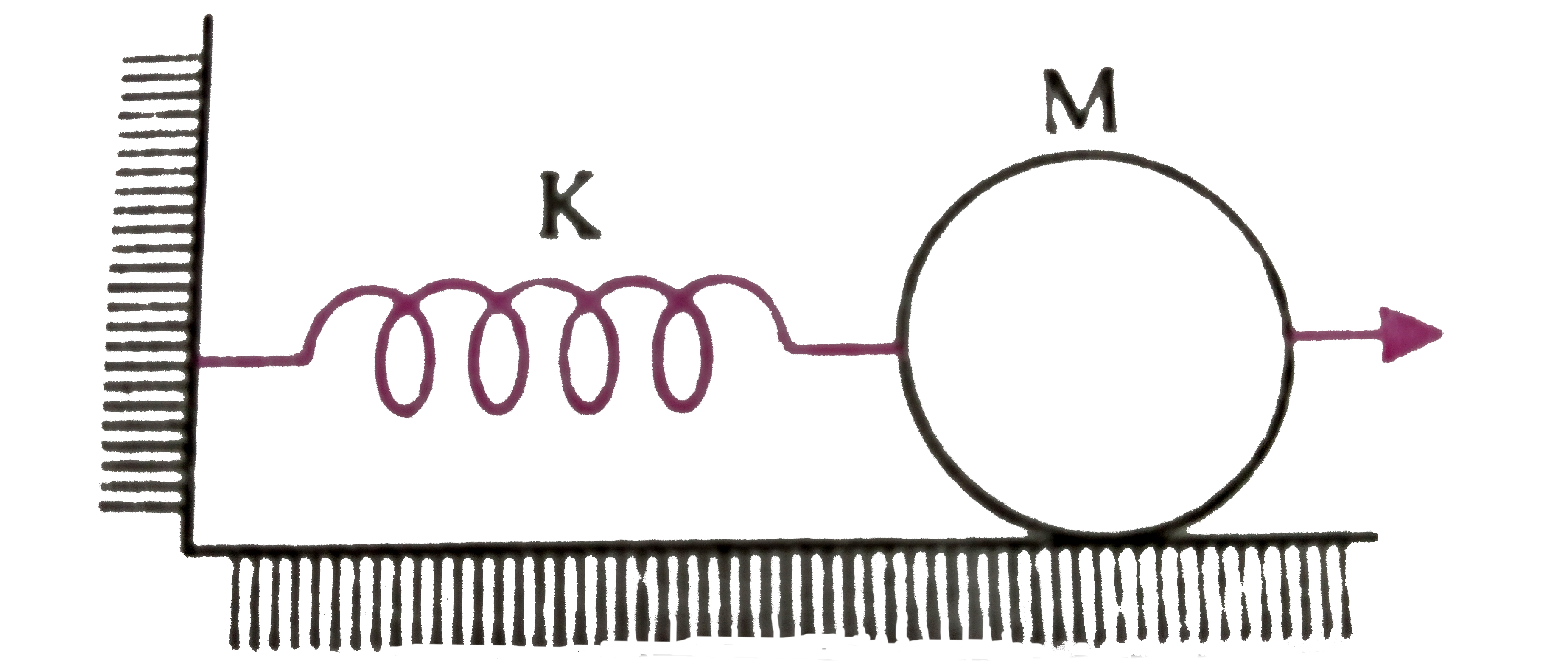 A2π√MKB2π√3MKC2π√M2KD2π√3M2K
A2π√MKB2π√3MKC2π√M2KD2π√3M2K - Question 2 - Select One
A solid cylinder of mass M and radius R rolls without slipping down an inclined plane of length L and height h. What is the speed of its center of mass when the cylinder reaches its bottom
A√34ghB√43ghC√4ghD√2gh - Question 3 - Select One
A solid uniform cylinder of mass M attached to a massless spring of force constant k is placed on a horizontal surface in such a way that cylinder can roll without slipping. If system is released from the stretched position of the spring, then the period will be-
_E01_059_Q01.png) A2π√MkB2π√3m2kC2π√M2kD2π√2M3k
A2π√MkB2π√3m2kC2π√M2kD2π√2M3k

A uniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force F is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder isView SolutionA solid cylinder of mass M and radius R rolls without slipping on a flat horizontal surface. Its moment of inertia about the line of contact is ?
View SolutionA solid cylinder of mass M and radius R rolls without slipping down an inclined plane of length L and height h. What is the speed of its centre of mass when the cylinder reaches its bottom ?
View SolutionA solid cylinder of mass M and radius R rolls without slipping down on inclined plane of length L and height h what is the speed of its centre of mass when the cylinder reaches its bottom?
View SolutionA solid cylinder of mass M and radius R rolls without slipping down on inclined plane of length L and height h what is the speed of its centre of mass when the cylinder reaches its bottom?
View Solution

