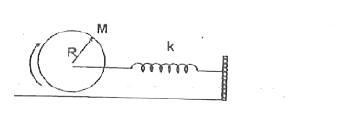
A solid cylinder of mass m is attached to a horizontal spring with force constant k. The cylinder can roll without slipping along the horizontal plane. (See the accompanying figure.) Show that the center of mass of the cylinder executes simple harmonic motion with a period T=2π√3m2k, if displaced from mean position.

Let at any position, x be the extension in the spring and v be the velocity of centre of mass of the cylinder. Then,
P.E. of spring U=12kx2
K.E. of translation, KT=12Mv2
K.E. of rotation, KR=12Iω2=14Mv2
[ ∵I=12Mr2 and v=ωr]
Total mechanical energy of the sysem is
E=U+KT+KR=12kx2+12Mv2+14Mv2
=12kx2+34Mv2...(i)
As per question , v=0, if x=0.25m , then
E+12×3×(0.25)+0=332J
At equilibrium position, U=0 [as x=0],
so from (i),
332=0+34Mv2 or Mv2=18J
At equilibrium position
(a) Translational K.E.
=12Mv2=12(18)=116J
(b) Rotational K.E.,
=14Mv2=14(18)=132J
(c) In SHM, the total energy is conserved,
so dEdt=0
From (i), we have
0=12k.2xdxdt+34M2vdvdt
or 34Md2xdt2=−12kx
[∵dxdt=v and dvdt=d2xdt2]
or d2xdt2=−2k3Mx ...(ii)
From (ii), we note that acceleration (d2x/dt2)∝x and is directed towards equilibrium position. Hence, the cylinder will execute SHM. Comparing (ii) with the equation
d2xdt2=−ω2x, we have
ω2=2k3M
or ω=√2k3M
Time period of SHM is,
T=2πω=2π√3M2k
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - conceptual problems
84 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Very Short Answer Questions
99 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - CURIOSITY QUESTION
2 Videos
- MATHEMATICAL TOOLSBOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks
5 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance
18 Videos
Similar Questions
A solid sphere of mass m is attached to a light spring of force constant k so that it can roll without slipping along a horizontal surface. Calculate the period of oscillation made by sphere.

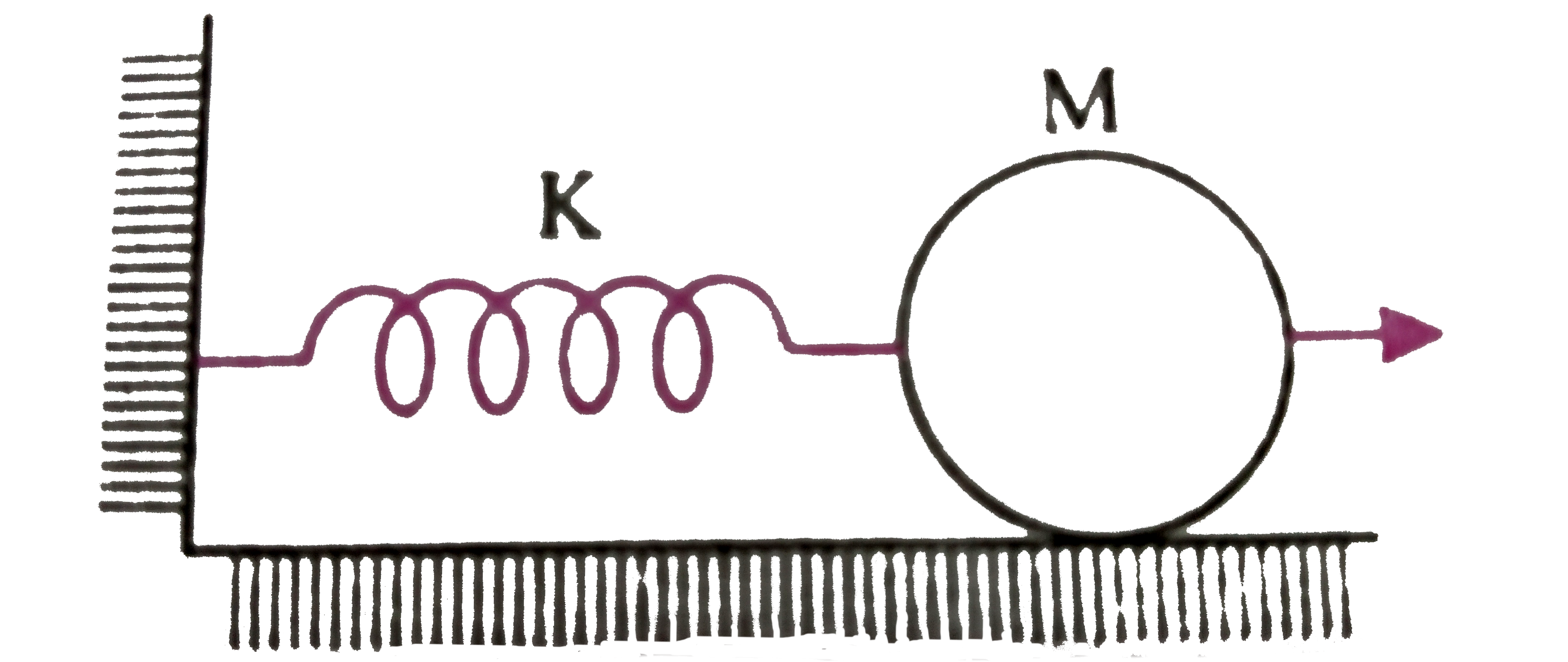
View SolutionA small solid cylinder of mass M attached to horizontal massless spring can roll without slipping along a horizontal surface. Show that if the cylinder is displaced slightly and released, it executes S.H.M. Also find its time period.
View Solution
Knowledge Check
A disc of mass M is attached to a horizontal massless spring of force constant K so that it can roll with out slipping along a horizontal surface. If the disc is pulled a little towards right and then released, its centre of mass executes SHM with a period of
 A2π√MKB2π√3MKC2π√M2KD2π√3M2K
A2π√MKB2π√3MKC2π√M2KD2π√3M2KA solid cylinder of mass M and radius R rolls without slipping down an inclined plane of length L and height h. What is the speed of its center of mass when the cylinder reaches its bottom
A√34ghB√43ghC√4ghD√2ghA solid uniform cylinder of mass M attached to a massless spring of force constant k is placed on a horizontal surface in such a way that cylinder can roll without slipping. If system is released from the stretched position of the spring, then the period will be-
_E01_059_Q01.png) A2π√MkB2π√3m2kC2π√M2kD2π√2M3k
A2π√MkB2π√3m2kC2π√M2kD2π√2M3k

A uniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force F is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder is
View SolutionA solid cylinder of mass M and radius R rolls without slipping on a flat horizontal surface. Its moment of inertia about the line of contact is ?
View SolutionA solid cylinder of mass M and radius R rolls without slipping down an inclined plane of length L and height h. What is the speed of its centre of mass when the cylinder reaches its bottom ?
View SolutionA solid cylinder of mass M and radius R rolls without slipping down on inclined plane of length L and height h what is the speed of its centre of mass when the cylinder reaches its bottom?
View SolutionA solid cylinder of mass M and radius R rolls without slipping down on inclined plane of length L and height h what is the speed of its centre of mass when the cylinder reaches its bottom?
View Solution
