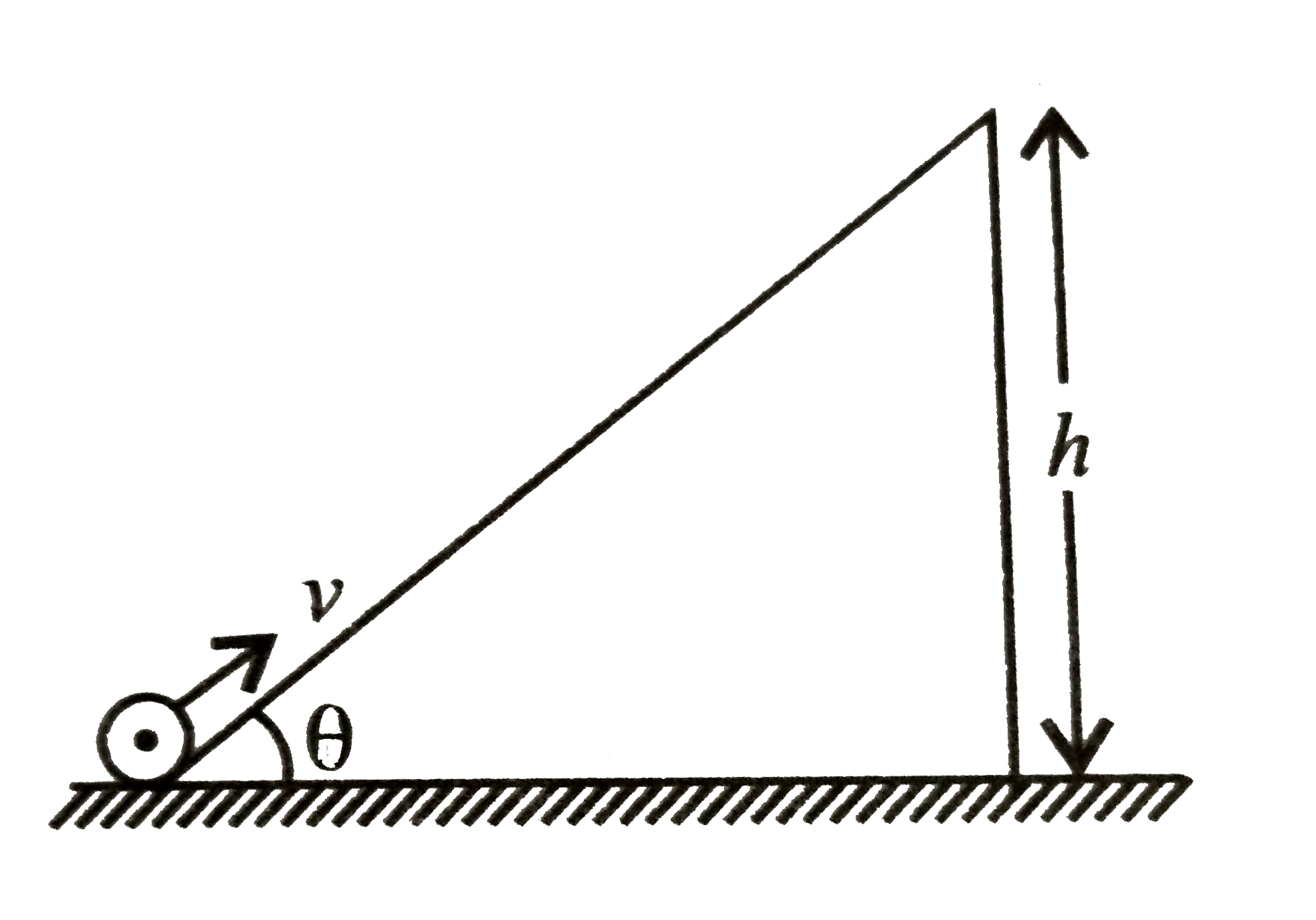
A solid cylinder rolls up an inclined plane of inclination $θ$ with an initial velocity $v$ . How far does the cylinder go up the plane ?

A

$\frac{3 v^{2}}{2 g sin θ}$

B

$\frac{v^{2}}{4 g sin θ}$

C

$\frac{3 v^{2}}{g sin θ}$

D

$\frac{3 v^{2}}{4 g sin θ}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Let the cylinder go up the plane upto a height h. Let M and R be the mass and radius of the cylinder respectively. According to law of conservation of mechanical energy, we get
$\frac{1}{2} M v^{2} + \frac{1}{2} I ω^{2} = M g h$
$\frac{1}{2} M v^{2} + \frac{1}{2} \frac{M R^{2}}{2} ω^{2} = M g h$ $∴$ For a solid cylinder $I = \frac{1}{2} M R^{2}$
$\frac{1}{2} M v^{2} + \frac{1}{4} M R^{2} ω^{2} = M g h$
$\frac{1}{2} M v^{2} + \frac{1}{4} M v^{2} = M g h (∴ v = R ω)$
$\frac{3}{4} M v^{2} = M g h$
$h = \frac{3 v^{2}}{4 g}$ ................(i)
Let s be distance travelled by the cylinder up the plane.
Then $sin θ = \frac{h}{s}$ or $s = \frac{h}{sin θ} = \frac{3 v^{2}}{4 g sin θ}$ (using (i))

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A solid cylinder roll up without slipping an inclined plane of inclination $θ$ with an initial velocity v. How for does the cylinder go up the plane :-
A $\frac{3 v^{2}}{2 g sin θ}$
B $\frac{v^{2}}{4 g sin θ}$
C $\frac{3 v^{2}}{g sin θ}$
D $\frac{3 v^{2}}{4 v sin θ}$
Question 2 - Select One or More
A solid cylinder is rolling down a rough inclined plane of inclination $θ$ . Then
AThe friction force is dissipative
BThe friction force is necessarily changing
CThe friction force will aid rotation but hinder translation
DThe friction force is reduced if $θ$ is reduced
Question 3 - Select One
If a solid cylinder rolls down an inclined plane, then its:
Arotational energy is $1 / 3$ and the translational energy $2 / 3$ of its total K.E.
Btranslational energy is $1 / 3$ and rotational energy is $2 / 3$ of its total K.E.
Crotational and translational energies are equal.
Dentire energy is rotational K.E.

NCERT FINGERTIPS-SYSTEM OF PARTICLES AND ROTATIONAL MOTIONS-Rolling Motion

Home
Ask Doubt
Profile