A solid cylinder with r=0.1m and mass M=2kg is placed such that it is in contact with the vertical and a horizontal surface as shown in Fig. The coefficient of friction is μ=(1/3) for both the surfaces. Find the distance (in CM) from the centre of the cylinder at .which a force F=40N should be applied vertically so that the cylinder just starts rotating in anticlockwise direction.

The correct Answer is:6
For equilibrium of the cylinder in the horizontal direction
N1=μN2……….i

In the vertical direction
N2+μN1=F+mg…….ii
Solving these two equations with F=40N,M=2kg and μ=13, we get
N1=18N
and N2=54N
Now, Fd=μ(N1+N1)r
∴d=M(N1+N2)rF
=(13)(18+50)(0.1)40=0.06m
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Linked Comprehension
28 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
A block of mass 1 kg is held at rest against a rough vertical surface by pushing by a force F horizontally. The coefficient of friction is 0.5. When

View SolutionA block of mass 20kg is placed on a rough horizontal plane and a horizontal force of 12N is applied. If coefficient of friction is 0.1 the frictional force acting on it is,
View Solution
Knowledge Check
Two blocks A and B of masses 10 kg and 15 kg are placed in contact with each other rest on a rough horizontal surface as shown in the figure. The coefficient of friction between the blocks and surface is 0.2. A horizontal force of 200 N is applied to block A. The acceleration of the system is (Take g=10ms−2)
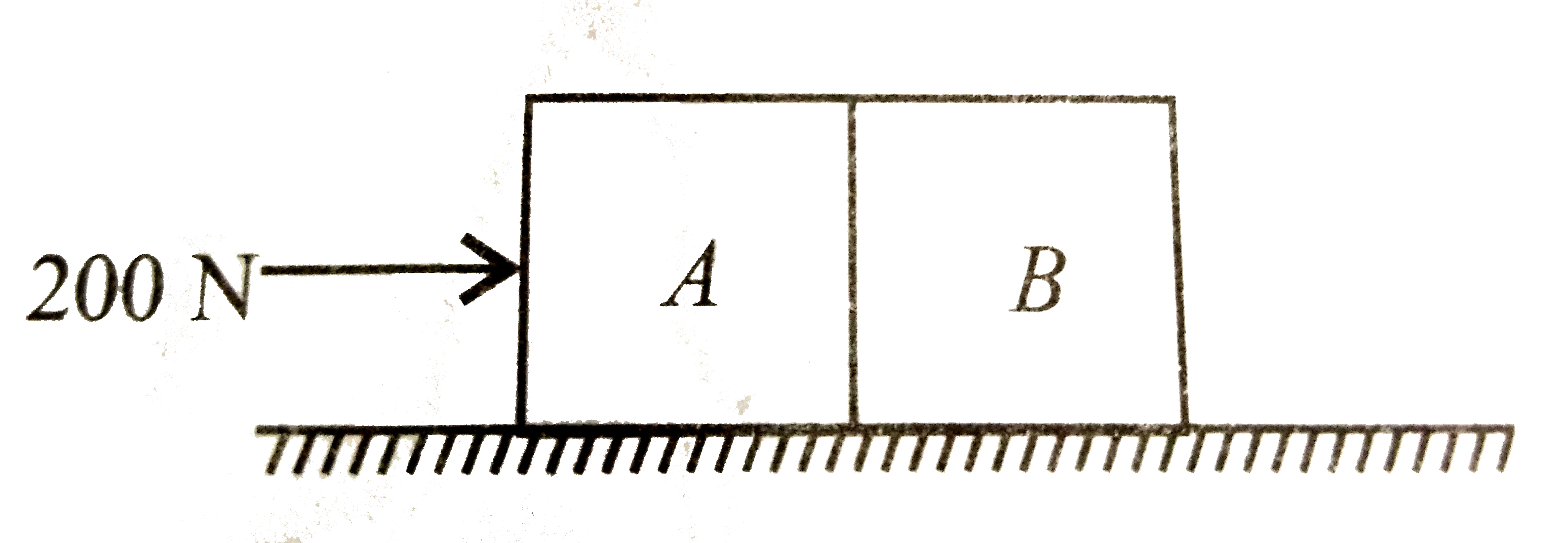 A4ms−2B6ms−2C8ms−2D10ms−2
A4ms−2B6ms−2C8ms−2D10ms−2
A block is kept on a rough horizontal surface as shown. Its mass is 2 kg and coefficient of friction between block and surface (μ)=0.5. A horizontal force F is acting on the block. When

View SolutionA block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the will be.
View SolutionA block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the will be.
View SolutionA block mass m=2kg is accelerating by a force F=20N applied on a smooth light pully as shown in fig 7.86 If the coefficient of kinetic friction between the block and the surface is μ=0.3 find its acceleration

View SolutionTwo blocks of masses 1 kg and 2 kg are placed in contact on a smooth horizontal surface as shown in fig. A horizontal force of 6N is applied d(a) on a 1-kg block. Find the force of interaction of the blocks.

 .
.
View SolutionA force F is applied at the centre of a disc of mass M. The minimum value of coefficient of friction of the surface for rolling is
View SolutionA force F is applied horizontally on a cylinder in the line of centre as shown in the figure. The cylinder is on a rough surface of coefficient of fricition μ. The direction of the friction force acting on the cylinder will be
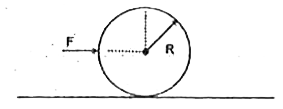
View Solution
