A solid sphere has a uniformly distributed mass of 1.0×104g and a radius of 1.0 m. What is the magnitude of the gravitational force due to the sphere on a particle of mass m = 2.0 kg when the particle is located at a distance of (a) 1.5 m and (b) 0.50 m from the center of the sphere? (c) Write a general expression for the magnitude of the gravitational force on the particle at a distance r≤1.0 , from the center of the sphere.
(a) 5.9×10−7N, (b) 6.7×10−7N, (c ) (1.3×10−6N/m)r
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)16videos
GRAVITATION
- BOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)7videos
GRAVITATION
- BOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - CHECKPOINT5videos
GRAVITATION
- BOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFRACTIONEXERCISE - Practice questions(Integers)4videos
GEOMETRICAL OPTICS : REFRACTION
- BOOK - RESNICK AND HALLIDAYCHAPTER - HEAT-MEASUREMENT AND TRANSFEREXERCISE - PRACTICE QUESTIONS( INTEGER TYPE)5videos
HEAT-MEASUREMENT AND TRANSFER
Similar Questions
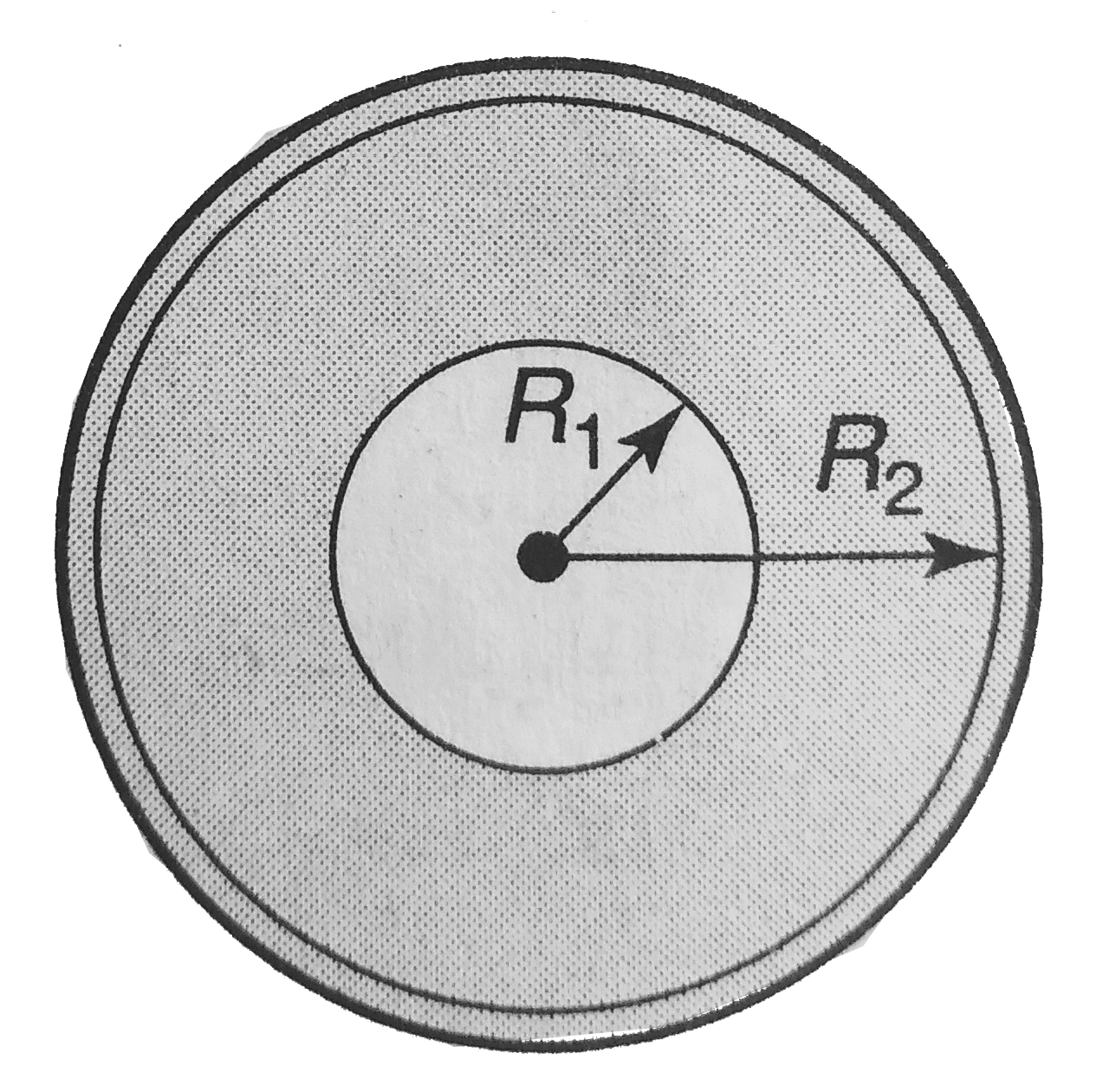
A spherical shell has inner radius R1, outer radius R2, and mass M, distributed uniformly throughout the shell. The magnitude of the gravitational force exerted on the shell by a point mass particle of mass m, located at a distance d from the center, inside the inner radius, is:
View SolutionThe masses of two spheres are 10 kg and 20 kg respectively. If the distance between their centres is 100 m, find the magnitude of the gravitational force between them.
View Solution
Knowledge Check
- Question 1 - Select One
A spherical shell has inner radius R1, outer radius R2, and mass M, distributed uniformly throughout the shell. The magnitude of the gravitational force exerted on the shell by a point mass particle of mass m, located at a distance d from the center, inside the inner radius, is:
A0BGMm/R21CGMm/d2DGMm/(R22−d2)
The masses of two spheres are 10 kg and 20 kg respectively. If the distance between their centres is 100m, find the magnitude of the gravitational force between them.
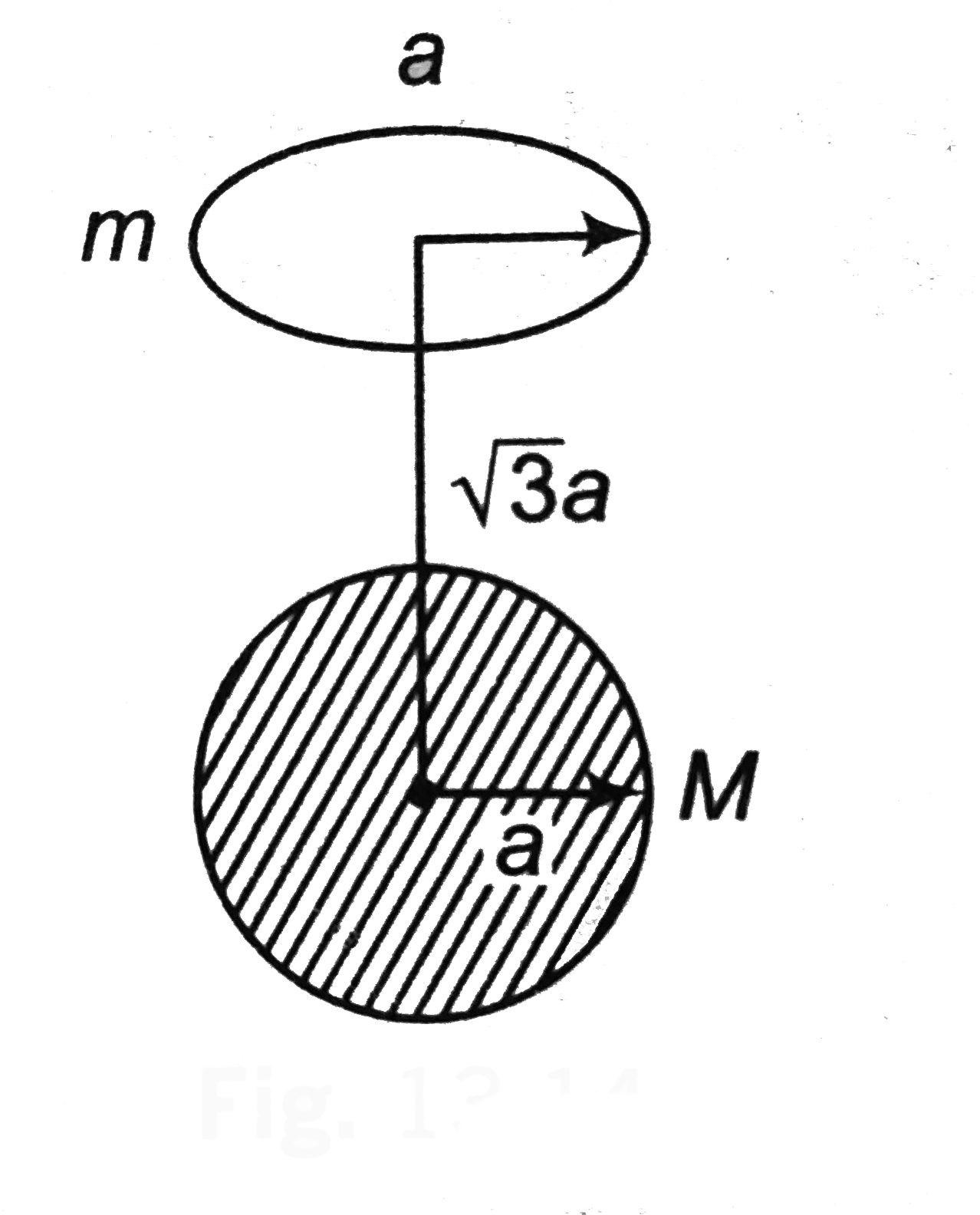
View SolutionA uniform ring of mass m is lying at a distance √3 a from the centre of mass M just over the sphere (where a is the radius of the ring as well as that of the sphere). Find the magnitude of gravitational force between them .
 View Solution
View SolutionA uniform ring of mass m is lying at a distance √3 a from the centre of mass M just over the sphere (where a is the radius of the ring as well as that of the sphere). Find the magnitude of gravitational force between them .
 View Solution
View SolutionA solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in the figure. A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if

x>2RView SolutionA particle of mass 1kg is kept on the surface of a uniform sphere of mass 20kg and radius 1.0m. Find the work to be done against the gravitational force between them to take the particle away from the sphere.
View SolutionA particle of mass 1kg is kept on the surface of a uniform sphere of mass 20kg and radius 1.0m. Find the work to be done against the gravitational force between them to take the particle away from the sphere.
View SolutionA sphare of mass M and radiusR2 has a concentric cavity of radius R1 as shown in figure The force F exerted by the sphere on a particle of mass m located at a distance r from the centre of sphere veries as (0≤r≤∞) .
 View Solution
View Solution

