A particle is to be placed, in turn, outside four objects each of mass m:(1) a large uniform solid sphere, (2) a large uniform spherical shell,(3) a small uniform solid sphere, and (4) a small uniform shell. In each situation,the distance between the particle and the center of the object is d. Rank the objects according tothe magnitude of the gravitational force they exert on the particle, greatest first.
All tie
Topper's Solved these Questions
- GRAVITATIONBOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - PROBLEMS
63 Videos
- GRAVITATIONBOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)
16 Videos
- GRAVITATIONBOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)
4 Videos
- GEOMETRICAL OPTICS : REFRACTIONBOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFRACTIONEXERCISE - Practice questions(Integers)
4 Videos
- HEAT-MEASUREMENT AND TRANSFERBOOK - RESNICK AND HALLIDAYCHAPTER - HEAT-MEASUREMENT AND TRANSFEREXERCISE - PRACTICE QUESTIONS( INTEGER TYPE)
5 Videos
Similar Questions
A particle of mass m is located outside a uniform sphere of mass M at a distance r from its centre. Find:
(a) the potential energy of gravitational interaction of the particle and the sphere,
(b) the gravitational force which the sphere exerts on the particle.
View SolutionA uniform solid sphere of mass m and radius r is suspended symmetrically by a uniform thin spherical shell of radius 2r and mass m.
View Solution
Knowledge Check
Three uniform spheres each of mass m and diameter D are kept in such a way that each touches the other two, then magnitudes of the gravitational force on any one sphere due to the other two is
A3Gm2D2B2√3Gm2D2C√3Gm24D2D√3Gm2D2A uniform solid sphere of mass m and radius r is suspended symmetrically by a uniform thin spherical shell of radius 2r and mass m.
AThe gravitational field at a distance of 1.5r from the centre is 29Gmr2BThe gravitational field at a distance of 2.5r from centre is 825Gmr2CThe gravitational field at a distance of 1.5r from centre is zeroDThe gravitational field between the sphere and spherical shell is uniform.A uniform ring of mass m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The centre of the ring is at distance √3a from the centre of the sphere. Find the gravitational force exerted by the sphere on the ring.
AGMm8r2BGMm4r2C√3GMm8r2DGMm8r3√3
A uniform ring of mas m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The center of the ring is at a distance √3a from the center of the sphere. Find the gravitational force exerted by the sphere on the ring.
View SolutionA uniform ring of mas m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The centre of the ring is at a distance √3 a from the centre of the sphere. Find the gravitational force exerted by the sphere on the ring.
View SolutionA solid sphere of mass m radius r is placed inside a hollow thin spherical shell of mass M and radius 2r as shown in figure. A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if
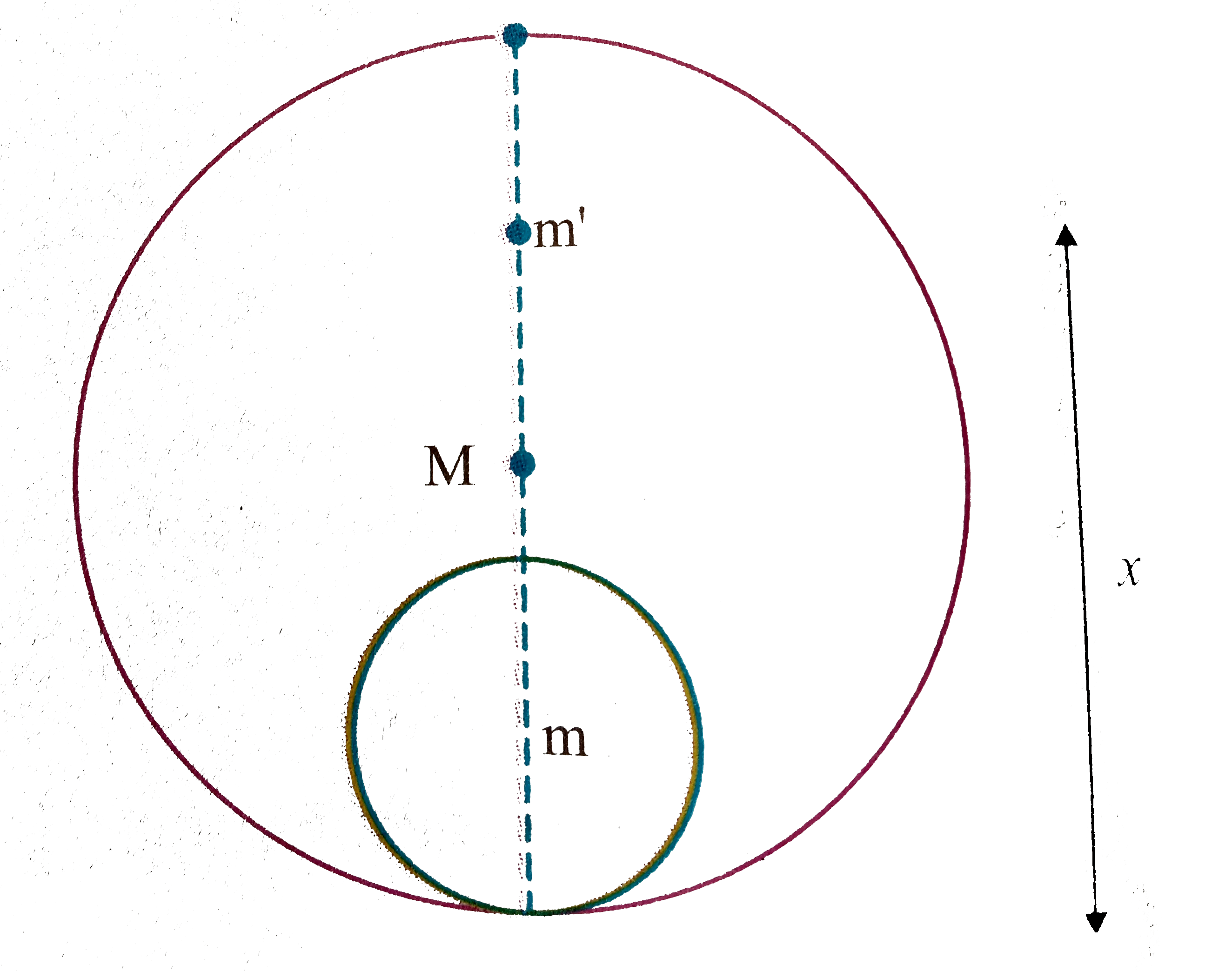
2r<x<2R
View SolutionA solid sphere of mass m radius r is placed inside a hollow thin spherical shell of mass M and radius 2r as shown in figure. A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if

x>2R
View SolutionA solid sphere of mass m and radius r is placed inside a hollow thin spherical shell of mass M and radius R as shown in the figure. A particle of mass m' is placed on the line joining the two centres at a distance x from the point of contact of the sphere and the shell. Find the magnitude of the resultant gravitational force on this particle due to the sphere and the shell if

r<x<2r
View Solution
