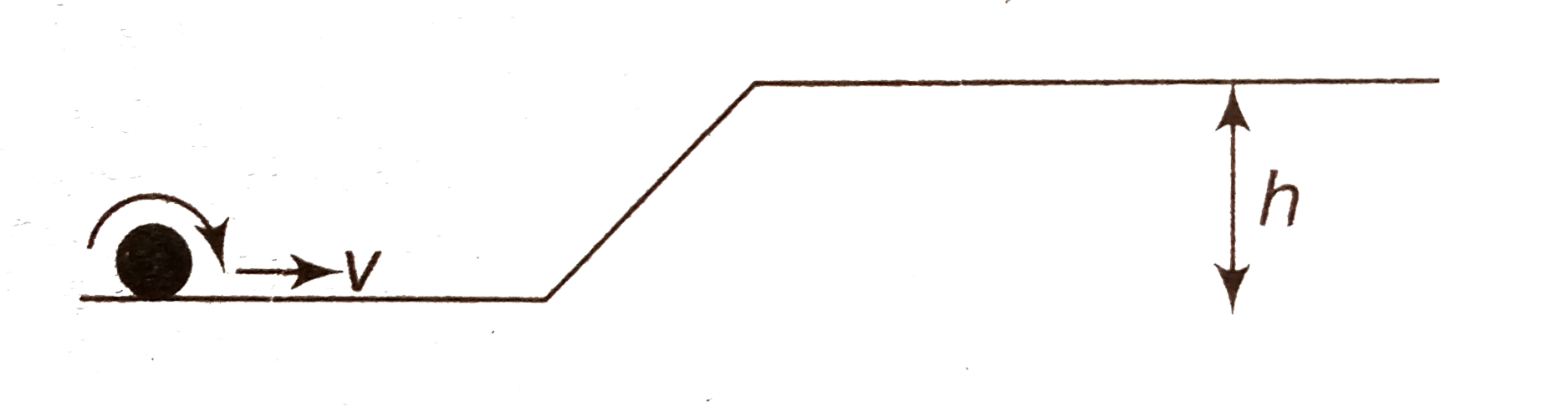
A solid sphere is rolling on a frictionless surface, shown in figure with a translational velocity $v m / s$ . If it is to climb the inclined surface then $v$ should be :

$2 g h$

$\frac{10}{7} g h$

$> \sqrt{2 g h}$

$\geq \sqrt{\frac{10}{7} g h}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Updated on:21/07/2023

A solid sphere is rolling on a frictionless surface, shown in figure with a translational velocity $v m / s$ . If is to climb the inclind surface then $v$ should be :

A(1) $\geq \sqrt{\frac{10}{7} g h}$
B $\geq \sqrt{2 g h}$
C $2 g h$
D $\frac{10}{7} g h$
A solid sphere is rolling down an inclined plane. Then the ratio of its translational kinetic energy to its rotational kinetic energy is
A2.5
B1.5
C1
D0.4
A sphere is moving on a smooth surface with linear speed $v_{0}$ and angular velocity $ω_{0}$ . It finds a rough inclined surface and it starts climbing up:

Aif $v_{0} > R ω_{0}$ friction force will act downwards
Bif $v_{0} < R ω_{0}$ , frictio force will act upwards
Cif $v_{0} = R ω_{0}$ no friction force will act
Dif all above case friction will act upwards