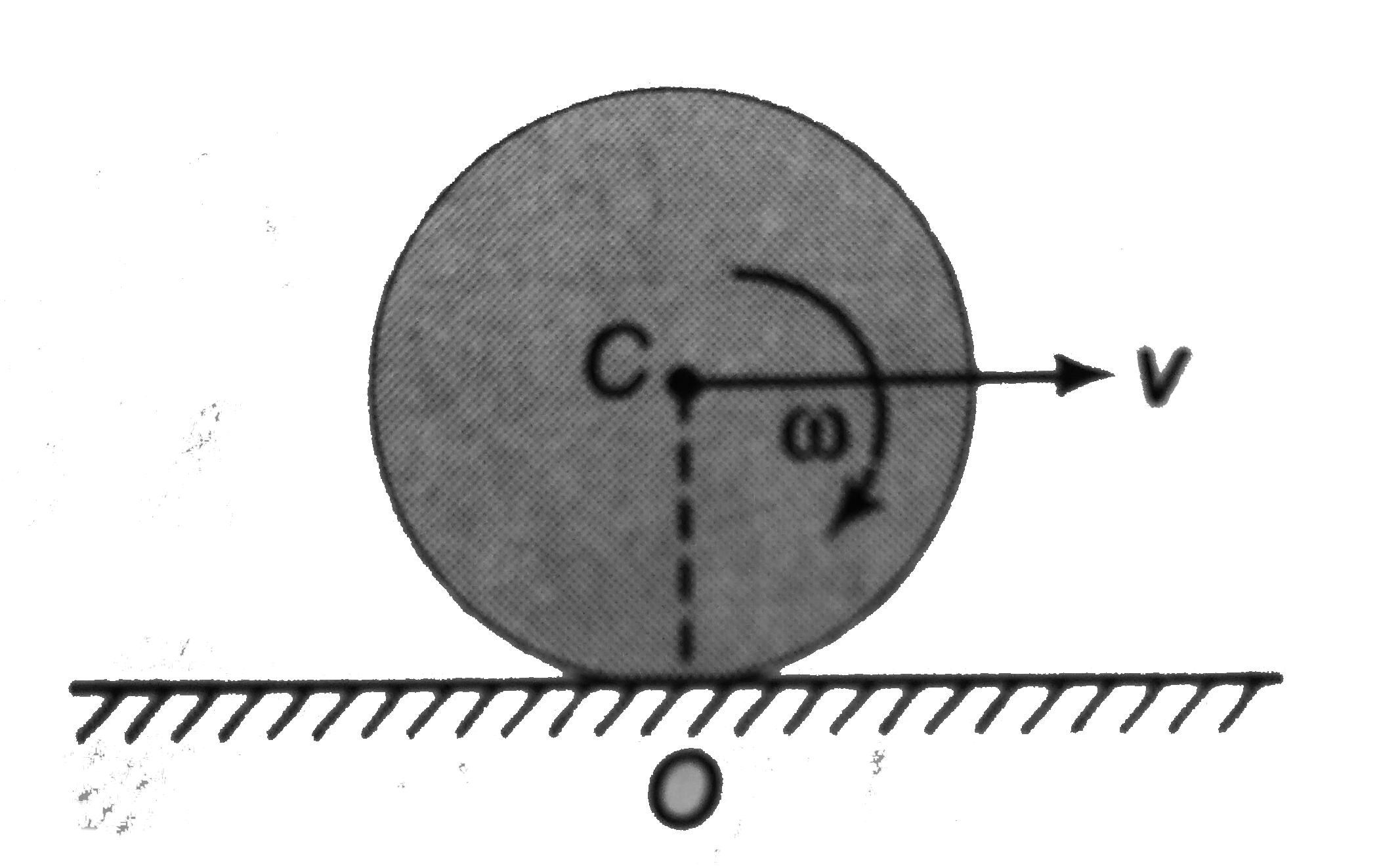
A solid sphere is rolling without slipping as shown in figure. Prove that
12mv2+12lCω2=12l0ω2
IC=25mR2,I0=75mR2 and ω=vR
substituting these values in the given equation we get the result.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercise 12.105videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercise 12.112videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercise 12.83videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises39videos
ROTATION
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions17videos
ROTATIONAL MOTION
Similar Questions
A 1 Kg solid sphere rolls without slipping on a rough horizontal suface as shown in figure. Select incorrect alternative
 View Solution
View SolutionWithout expanding at any stage, prove that ∣∣ ∣ ∣∣1ωω2ωω21ω21ω∣∣ ∣ ∣∣= 0
View SolutionIf 1,ω,ω2 are three cube roots of unity, prove that
11+ω+11+ω2=1View SolutionIf 1,x1,x2,x3 are the roots of x4−1=0andω is a complex cube root of unity, find the value of (ω2−x1)(ω2−x2)(ω2−x3)(ω−x1)(ω−x2)(ω−x3)
View Solution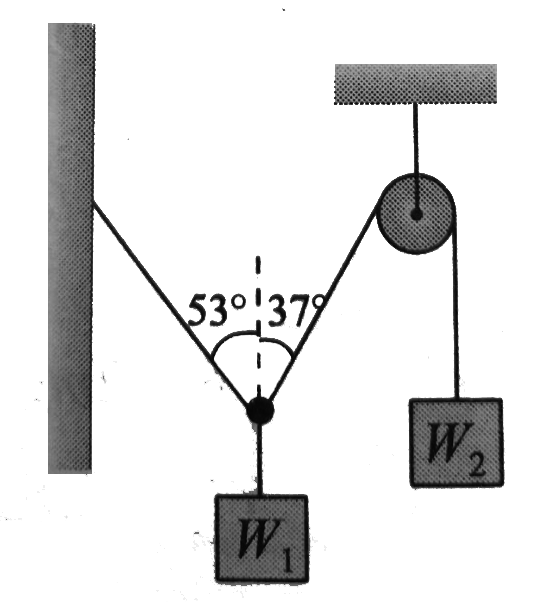
Two weights W1 and W2 in equilibrius and at rest are suspended as shown in figure. Then the ratio W1W2 is:View SolutionA : When a ring moves in pure rolling condition on ground it has 50% translational and 50% rotational energy.
R : KEtransKErot=12MV212lω2=12MV212(MR2)V2R2=1:1View Solutionif tanθ+secθ=l then prove that secθ=l2+12l
View Solutionif tanθ+secθ=l then prove that secθ=l2+12l
View SolutionIf 1,ω,ω2 are cube roots of unity, prove that (x+y)2+(xω+yω2)2+(xω2+yω)2=6xy
View Solution
If the direction cosines of two lines are (l1,m1,n1) and
(l2,m2,n2) and the angle between them is θ then
l21+m21+n21=1=l22+m22+n22
and costheta=l1l2+m1m2+n1n2
If the angle between the lines is 60∘ then the value
of l1(l1+l2)+m1(m1+m2)+n1(n1+n2) isView Solution

