A : When a ring moves in pure rolling condition on ground it has 50% translational and 50% rotational energy.
R : KEtransKErot=12MV212lω2=12MV212(MR2)V2R2=1:1
If both Assertion & Reason are true and the reason is the correct explanation of the assertion,
If both Assertion & Reason are true but the reason is not the correct explanation of the assertion,
If Assertion is true statement but Reason is false,
If both Assertion and Reason are false statements,
The correct Answer is:A
To solve the given assertion and reason question, we will analyze the kinetic energies involved in the rolling motion of a ring.
1. Understanding the Motion:
- When a ring rolls without slipping on the ground, it exhibits both translational and rotational motion. The translational motion refers to the movement of the center of mass of the ring, while the rotational motion refers to the spinning of the ring around its center.
2. Kinetic Energy Formulas:
- The translational kinetic energy (KE_trans) of the ring is given by:
KEtrans=12mv2
where m is the mass of the ring and v is the linear velocity of the center of mass.
- The rotational kinetic energy (KE_rot) of the ring is given by:
KErot=12Iω2
where I is the moment of inertia of the ring and ω is the angular velocity.
3. Moment of Inertia of the Ring:
- The moment of inertia I for a ring about its central axis is:
I=mR2
where R is the radius of the ring.
4. Relating Linear and Angular Velocity:
- In pure rolling motion, the relationship between linear velocity v and angular velocity ω is:
v=Rω⇒ω=vR
5. Substituting into the Rotational Kinetic Energy:
- Now substituting ω into the rotational kinetic energy formula:
KErot=12Iω2=12(mR2)(vR)2=12mR2⋅v2R2=12mv2
6. Finding the Ratio of Kinetic Energies:
- Now, we can find the ratio of translational kinetic energy to rotational kinetic energy:
KEtransKErot=12mv212mv2=1
7. Conclusion:
- Since the ratio of translational kinetic energy to rotational kinetic energy is 1:1, this means that both energies are equal when the ring is rolling without slipping. Hence, the assertion that the ring has 50% translational and 50% rotational energy is true.
Final Answer:
Both the assertion (A) and reason (R) are true, and the reason correctly explains the assertion.
---
- When a ring rolls without slipping on the ground, it exhibits both translational and rotational motion. The translational motion refers to the movement of the center of mass of the ring, while the rotational motion refers to the spinning of the ring around its center.
- The translational kinetic energy (KE_trans) of the ring is given by:
KEtrans=12mv2
where m is the mass of the ring and v is the linear velocity of the center of mass.
- The rotational kinetic energy (KE_rot) of the ring is given by:
KErot=12Iω2
where I is the moment of inertia of the ring and ω is the angular velocity.
- The moment of inertia I for a ring about its central axis is:
I=mR2
where R is the radius of the ring.
- In pure rolling motion, the relationship between linear velocity v and angular velocity ω is:
v=Rω⇒ω=vR
- Now substituting ω into the rotational kinetic energy formula:
KErot=12Iω2=12(mR2)(vR)2=12mR2⋅v2R2=12mv2
- Now, we can find the ratio of translational kinetic energy to rotational kinetic energy:
KEtransKErot=12mv212mv2=1
- Since the ratio of translational kinetic energy to rotational kinetic energy is 1:1, this means that both energies are equal when the ring is rolling without slipping. Hence, the assertion that the ring has 50% translational and 50% rotational energy is true.
Both the assertion (A) and reason (R) are true, and the reason correctly explains the assertion.
Similar Questions
The value of 1r21+1r22+1r32+1r2, is
View SolutionShow that (1r1+1r2)(1r2+1r3)(1r3+1r1)=64R3a2b2c2
View Solution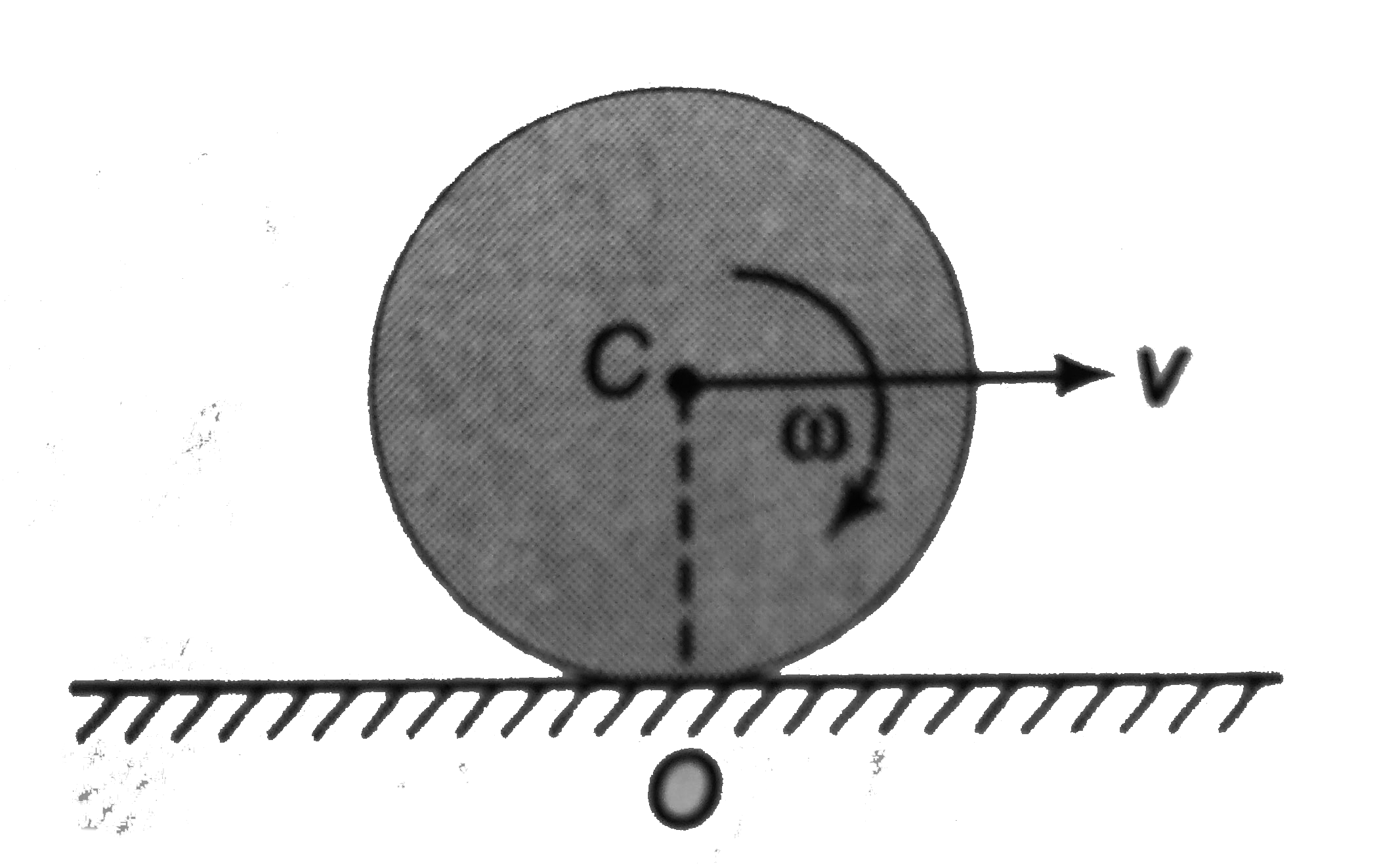
A solid sphere is rolling without slipping as shown in figure. Prove that
12mv2+12lCω2=12l0ω2View SolutionFor example , at the time t=0 , the particle is at its mean position, then at which times, the particle will have potential energy 50% of its total energy within t=0 to t=T ?
Hint : When PE is 50% of total energy 12kx2=12.12kA2View SolutionValue of 1r21'+1r22+1r23+1r2 is :
View SolutionCalculate the frequency of paritcle wave, when the kinetic energy of a sub-atomic particle is3.79×10−27J.
Hint :KE=12mv2
λ=hmv,λ=vv
∴vv=hmv,v=mv2h=2×12mv2hView SolutionFor Question , calculat the block's speed asit passes through the equilibrium point ?
Hint :E=K+U=12mv2+12kx2=12mv2+0 . Calculate vView SolutionThe circles having radii r1andr2 intersect orthogonally. The length of their common chord is 2r1r2√r12+r22 (b) √r12+r222r1r2 r1r2√r12+r12 (d) √r12+r12r1r2
View SolutionThe sum of coefficients of integral powers of x in the binomial expansion of (1−2√x)50 is: (1) 12(350+1) (2) 12(350) (3) 12(350−1) (4) 12(250+1)
View SolutionFind the sum ∞∑r=1tan−1(2(2r−1)4+r2(r2−2r+1))
View Solution

