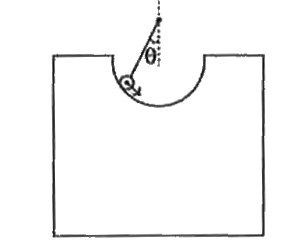
A solid sphere is rolling without slipping on a semi-circular track of radius 10m as shown in the figure. The radius of solid sphere is much smaller than the radius of semi-circular track. At the lowest point, it has a velocity 10 m/s. To what maximum angle θ from the vertical will the sphere travel before it comes back down? Neglect the rolling friction between the sphere and the track. (Take g=10m/s2)
 Solution in Telugu
Solution in Telugu
sin−1(35)
sin−1(37)
cos−1(310)
cos−1(13)
The correct Answer is:C
As there is no slip, energy is conserved So, mechanical energy of ball at bottom= mechanical energy of ball at top
⇒mgr+12mv2COM+12ICOMω2=mgh
⇒34v2=g(h−r)[∴I=mr22andv=rω]
and r can be neglected.
so, h=3v24g
Also, h−R(1−cosθ)⇒3v24g=R(1−cosθ) with value, we get
cosθ=310⇒θ=cos−1(310)
Topper's Solved these Questions
Similar Questions
If A represents density, B represents velocity, C represents specific heat capacity and D represents wavelength, then the quantity having the dimensions of product of A, B, C and D is
View SolutionMatch the entries in List I with those in List II.

View SolutionThe ratio of the accelerations for a solid sphere (mass m, and radius R ) rolling down an incline of angle theta without slipping, and slipping down the incline without rolling is
View SolutionA block of mass M with a semi - circular track of radius R rests on a smooth floor. A sphere of mass m and radius r is released from rest from A . Find the velocity of sphere and track , when the sphere reaches B .
View SolutionA solid sphere is rolling without slipping on rough ground as shown in figure. If collides elastically with an identical another sphere at rest. There is no friction between the two spheres . Radius of each sphere is R and mass is m.
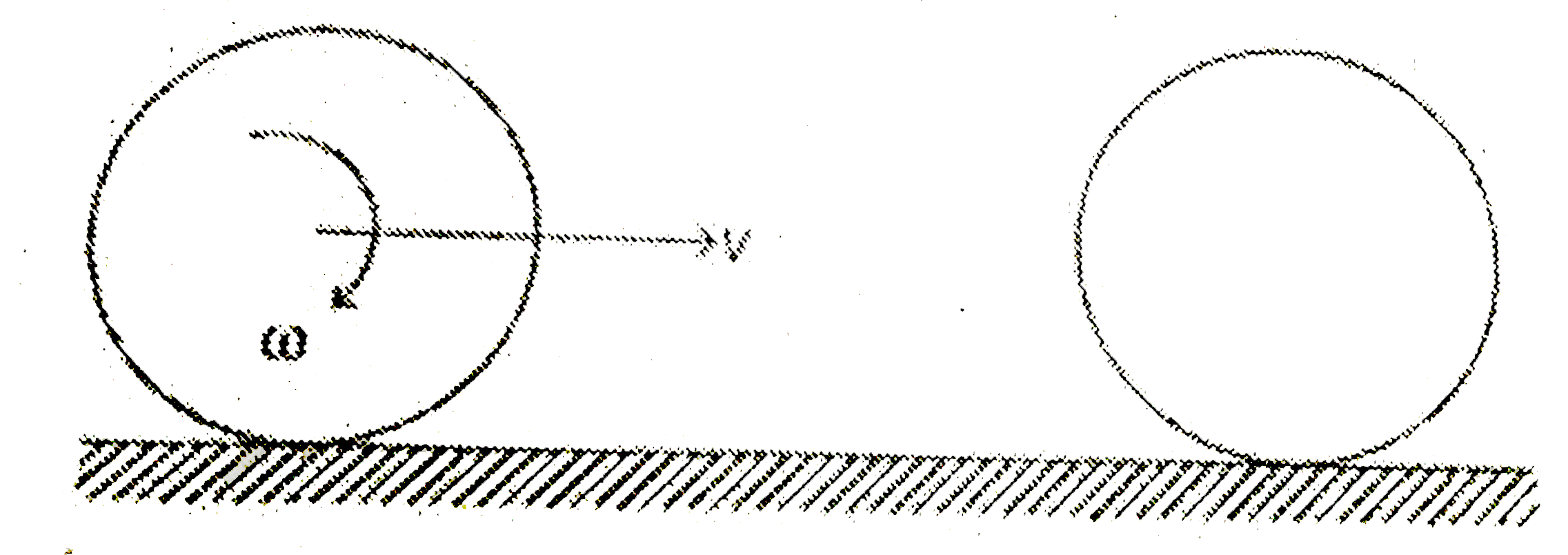
Linear velocity of first sphere after it again starts rolling without slipping is
View SolutionThe ratio of the acceleration for a solid sphere (mass m and radius R) rolling down an incline of angle θ without slipping and slipping down the incline without rolling is,
View SolutionA solid sphere is rolling without slipping on rough ground as shown in figure. It collides elastically with another identical sphere at rest. There is no friction between the two spheres. Radius of each sphere is R and mass is m. Linear velocity of first sphere after it again starts rolling without slipping is:
View SolutionA small solid sphere rolls without slipping along the track shown in figure. The sphere starts from rest from a height h above the bottom of a loop of radius R which is much larger than the radius of the sphere r. The minimum value of h for the sphere to complete the loop is:
View SolutionThe ratio of the acceleration for a solid sphere (mass m and radius R ) rolling down an incline of angle θ without slipping and slipping down the incline without rolling is
View SolutionThe ratio of the acceleration for a solid sphere (mass m and radius R) rolling down an incline of angle θ without slipping and slipping down the incline without rolling is,
View SolutionThe ratio of the acceleration for a solid sphere (mass .m. and radius .R.) rolling down and incline of angle .theta. without slipping and slipping down the incline without rolling is
View SolutionThe ratio of the accelerations for a solid sphere (mass m and radius R) rolling down an incline of angle theta without slipping and slipping down the incline without rolling is
View SolutionA solid cylinder of mass M and radius R rolls down an inclined plane of height h without slipping. The speed of its centre when it reaches the bottom is.
View SolutionThe ratio of the accelerations for a solid sphere (mass 'm' and radius 'R') rolling down and incline of angle θ without slipping and slipping down the incline without rolling is
View SolutionA solid sphere is rolling without slipping on rough ground as shown in figure. It collides elastically with an identical another sphere at rest. There is no friction between two spheres. Radius of each sphere is R and mass is m. Then linear velocity of first sphere (A) after it start rolling without slipping is
View Solution
