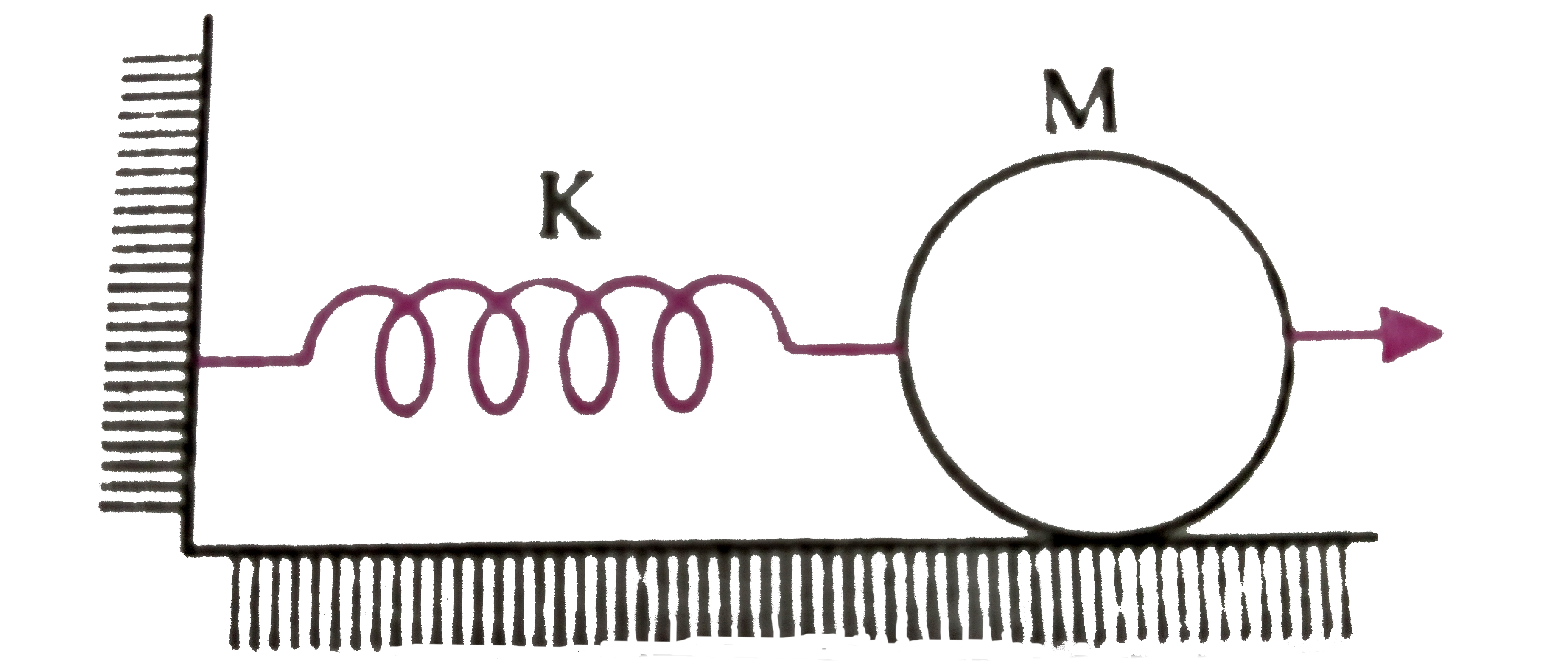
A solid sphere of mass M and Radius R is attached to a massless spring of force constant k as shown in the figure. The cylinder is pulled towards right slightly and released so that it executes simple harmonic motion of time period. If the cylinder rolls on the horizontal surface without slipping, calculate its time period of oscillation.

Total energy = translation K.E. + rotational k.E. + P.E. stored in spring
E=12mv2+12Iω2+12kx2
E=12mv2+12(25mR2)(vR)2+12kx2
⇒E=710mv2+12kx2
Now, the total energy of the sytem must remain constant, i.e., dEdt=0
We have dEdt=710m(2vdvdt)+12k(2xdxdt)=0
Now acceleration a=dvdt and velocity v=dxdt
Therefore, 75mva+kvx=0
or v(75ma+kx)=0
Since v≠0 we have
75ma+kx=0
or a=−(57km)x=−ω2x
where ω=√5k7m
Hence, time period T=2π√(7m)5k
Topper's Solved these Questions
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - NCERT FILE (Textbook Exercises)
19 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - NCERT (Additional Exercises)
6 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Conceptual Questions
18 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
Similar Questions
A small solid cylinder of mass M attached to horizontal massless spring can roll without slipping along a horizontal surface. Show that if the cylinder is displaced slightly and released, it executes S.H.M. Also find its time period.
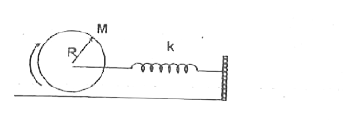
View SolutionA particle of mass m is attached with three springs A,B and C of equal force constancts k as shown in figure. The particle is pushed slightly against the spring C and released. Find the time period of oscillation.
 .
.
View Solution
Knowledge Check
A particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is
 A2π√mkB2π√m2kC2π√m3kDπ√mk
A2π√mkB2π√m2kC2π√m3kDπ√mkA particle of mass m is attached to three identical springs of spring constant k as shwon in figure. The time period of vertical oscillation of the particle is
 A2π√mkB2π√m2kC2π√m3kDπ√mk
A2π√mkB2π√m2kC2π√m3kDπ√mkA solid uniform cylinder of mass M attached to a massless spring of force constant k is placed on a horizontal surface in such a way that cylinder can roll without slipping. If system is released from the stretched position of the spring, then the period will be-
_E01_059_Q01.png) A2π√MkB2π√3m2kC2π√M2kD2π√2M3k
A2π√MkB2π√3m2kC2π√M2kD2π√2M3k
A particle of mass m is asttached to three springs A,B and C of equla force constants k as shown in figure. If the particle is pushed slightly against the spring C and released, find the time period of oscillastion.
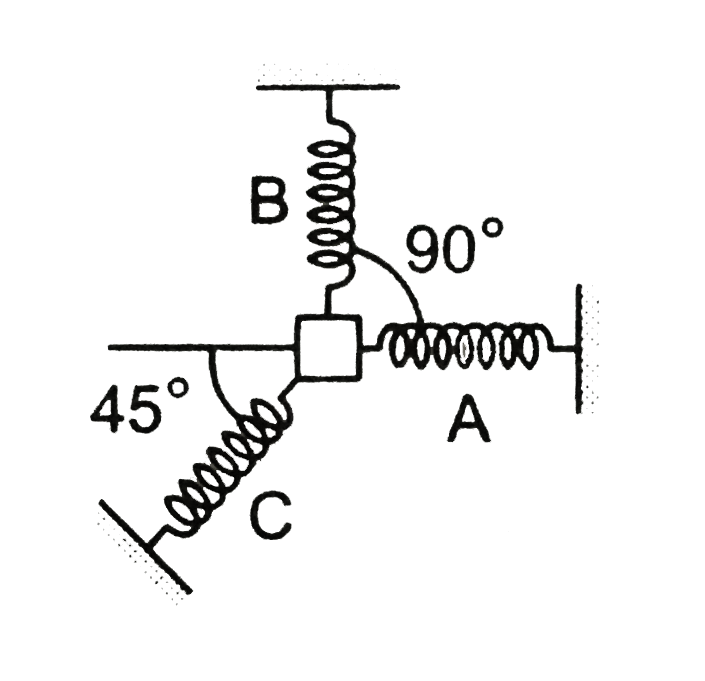
View SolutionA mass M is suspended from a spring of negligible mass. The spring is pulled a little then released, so that the mass executes simple harmonic motion of time period T. If the mass is increased by m, the time period becomes 5T3. Find the ratio of m/M.
View SolutionA solid sphere of mass m is attached to a light spring of force constant k so that it can roll without slipping along a horizontal surface. Calculate the period of oscillation made by sphere.

View SolutionA solid cylinder of mass M and radius R pure rolls on a rough surface as shown in the figure. Choose the correct alternative (s).

View SolutionA disc of mass M is attached to a horizontal massless spring of force constant K so that it can roll with out slipping along a horizontal surface. If the disc is pulled a little towards right and then released, its centre of mass executes SHM with a period of
View Solution
