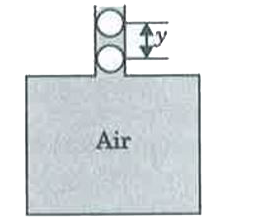
An air chamber of volume v has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction. Show that when the ball is pressed down a little and released for the time priod of oscillation, assuming pressure-volume variations of the air to be isothermal.
 ,
,
volume of chamber = V
Area of cross section of neck = a
mass of ball = m
Intially pressure
Let the ball be depressed by y units. Due to depression, there will be reduction in volume and hence, increase of pressure inside chamber.
∴ Decrease in volume of chamber = ΔV=ay
∴ Volumetric strain=ΔVV=ayV
∴B=Bk––mode–s=−PΔVV=−PVay
P=−BayV
Restoring force F=Pa
=−Ba2yV
As F=−Kx
∴ we can write k=Ba2V
T=2π√mVBa2
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - NCERT Exemplar Problems Subjective Question (Multiple Choice Questions (Type-I))11videos
OSCILLATIONS
- BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - NCERT Exemplar Problems Subjective Question (Multiple Choice Questions (Type-II))7videos
OSCILLATIONS
- BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - NCERT FILE (Textbook Exercises)19videos
OSCILLATIONS
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST16videos
MOTION IN A STRAIGHT LINE
- BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)6videos
PHYSICAL WORLD
Similar Questions
One end of a U-tube containing mercury is connected to a suction pump and the other end to atmosphere. A small pressure difference is maintained between the two columns. Show that, when the suction pump is removed, the column of mercury in the U-tube executes simple harmonic motion.
View SolutionAn air chamber of volume V has a neck area of cross section A into which a ball of mass m just fits and can move up and down without any friction, figure. Show that when the ball is pressed down a little and released, it executes SHM. Obtain an expression for the time periodof oscillations assuming pressure volume variatinos of air to be isothermal.
View Solution
Knowledge Check
- Question 1 - Select One
An air chamber of volume V has a neck area of cross section A into which a ball of mass m just fits and can move up and down without any friction, figure. Show that when the ball is pressed down a little and released, it executes SHM. Obtain an expression for the time period of oscillations assuming pressure volume variations of air to be isothermal.
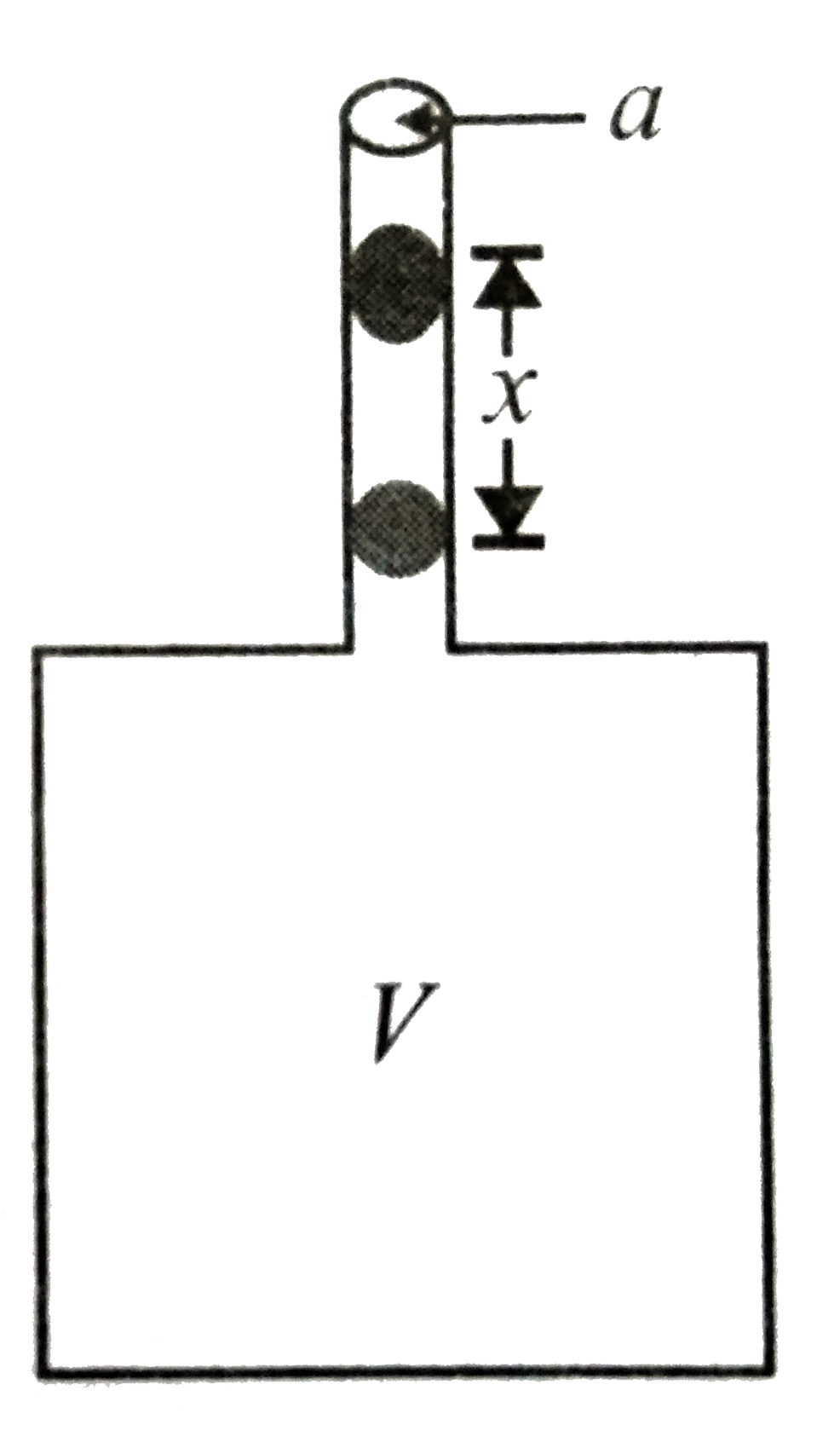 AT=2π√Ba2mVBT=2π√BVma2CT=2π√mBVa2DT=2π√mVBa2
AT=2π√Ba2mVBT=2π√BVma2CT=2π√mBVa2DT=2π√mVBa2 - Question 2 - Select One
An air chamber of volume V has a neck of cross-sectional area a into which a light ball of mass m just fits and can move up and down without friction. Consider diameter of the ball to be equal to that of the neck of the chamber. The ball is then pressed down a little and released. Let the bulk modulus of air is B. The time period of the oscillation of the ball is:
AT=2π√Ba2mVBT=2π√BVma2CT=2π√mBVa2DT=2π√mVBa2 - Question 3 - Select One
An air chamber of volume V has a long of cross sectional area A. A ball of mass m is fixed sympthlly in the track The ball modulus of air is B ball is pressed down slightly and released, the time period of the oscillation is
A2π√mV2BA2Bπ√2mVBA2C2π√mVBA2Dπ2√mBA2
An air chamber of volume V has a neck of crosssectional area "a' into which a light ball of mass "m' just fits and can move up and down without friction. The diameter of the ball is equal to that of the neck of the chamber. The ball is pressed down a little and released. If the bulk modulus of air is B the time period of the oscillation of the ball is 2πmxVyBza9. The value of xyq is
View SolutionA hollow cylindrical shell of radius R has mass M. It is completely filled with ice having mass m. It is placed on a horizontal floor connected to a spring (force constant k) as shown. When it is disturbed it performs oscillations without slipping on the floor.
(a) Find time period of oscillation assuming that the ice is tightly pressed against the inner surface of the cylinder.
(b) If the ice melts into non viscous water, find the time period of oscillations. (Neglect any volume change due to melting of ice)
 View Solution
View SolutionFigure shows initial state of an ideal gas trapped in a container with conducting walls and a piston (mass m) which can move without any friction. The container is placed on point supports and its wall are conducting. Assuming that atmospheric pressure is P0 and the mass of the ideal gas is negligible as compared to the mass of the piston and the mass of container. Take the cross section area of piston to be A. The piston is slowly lifted by an external agent and held in its position. Let M be the maximum mass of container so that it may "lift off" while pulling the piston upwards and Pi be the pressure of ideal gas in initial state. Pick the correct choice:
 View Solution
View SolutionA ideal gas is kept in a cylinder of cross sectional area A and volume v0. The mass of the gas enclosed is M and bulk modulus B. If the piston of the cylinder is pressed by small x, then find the time period of small oscillations,
View SolutionFigure shows initial state of an ideal gas trapped in a container with conducting walls and a piston (mass m) which can move without any friction. The container is placed on point supports and its wall are conducting. Assuming that atmospheric pressure is P0 and the mass of the ideal gas is negligible as compared to the mass of the piston and the mass of container. Take the cross section area of piston to be A. The piston is slowly lifted by an external agent and held in its position. Let M be the maximum mass of container so that it may "lift off" while pulling the piston upwards and Pi be the pressure of ideal gas in initial state. Pick the correct choice:
 View Solution
View Solution

