A solid sphere of mass m and radius R is moving with velocity of centre of massvˆi and angular velocity about centre ofmass ωˆi If the coefficient of friction between the sphere and ground μ the frictional force vectoris (consider v=ωR):
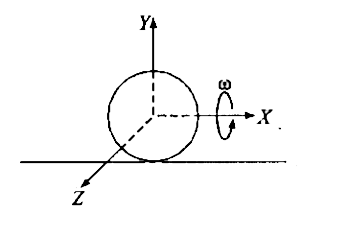
μmg(ˆi+ˆk)
μmg√2(ˆi+ˆk)
μmg√2(ˆk+ˆi)
μmgˆk
The correct Answer is:C
Step by step video, text & image solution for A solid sphere of mass m and radius R is moving with velocity of centre of massvhati and angular velocity about centre ofmass omegahati If the coefficient of friction between the sphere and ground mu the frictional force vectoris (consider v = omegaR): by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RIGID BODIES AND ROTATIONAL MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - paragraph
24 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - MCQ
16 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Conceptual MCQs Single Option Correct
39 Videos
- NEWTONS LAWS OF MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Unsolved Numerical Problem
81 Videos
- WORK, ENERGY AND POWERBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - unsolved
1 Videos
Similar Questions
A solid sphere of radius r and mass m rotates about an axis passing through its centre with angular velocity ω. Its K.E. Is
View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.

Force of friction between sphere and plank is
View Solution
Knowledge Check
A solid sphere with a velocity (of centre of mass) v and angular velocity ω is gently placed on a rough horizontal surface. The frictional force on the sphere :
Amust be forward (in direction of v)Bmust be backward (opposite to v)Ccannot be zeroDnone of the aboveA hollow sphere of mass m and radius R is rolling downdard on a rough inclined plane of inclination θ. If the coefficient of friction between the hollow sphere and incline is μ, then
AFriction opposes its translationBFriction supports rotation motionCOn decreasing θ, frictional force decreasesDAll of theseA ring and a solid sphere of same mass and radius are rotating with the same angular velocity about their diameteric axes then :-
Ait is easier to stop the ringBit is easier to stop the solid sphereCit is equally difficult to stop both of themDit is not possible to stop a rotating body
A solid sphere of mass m & radius R is cut into two equal parts and kept as shown. Find the height of centre of mass from the ground.
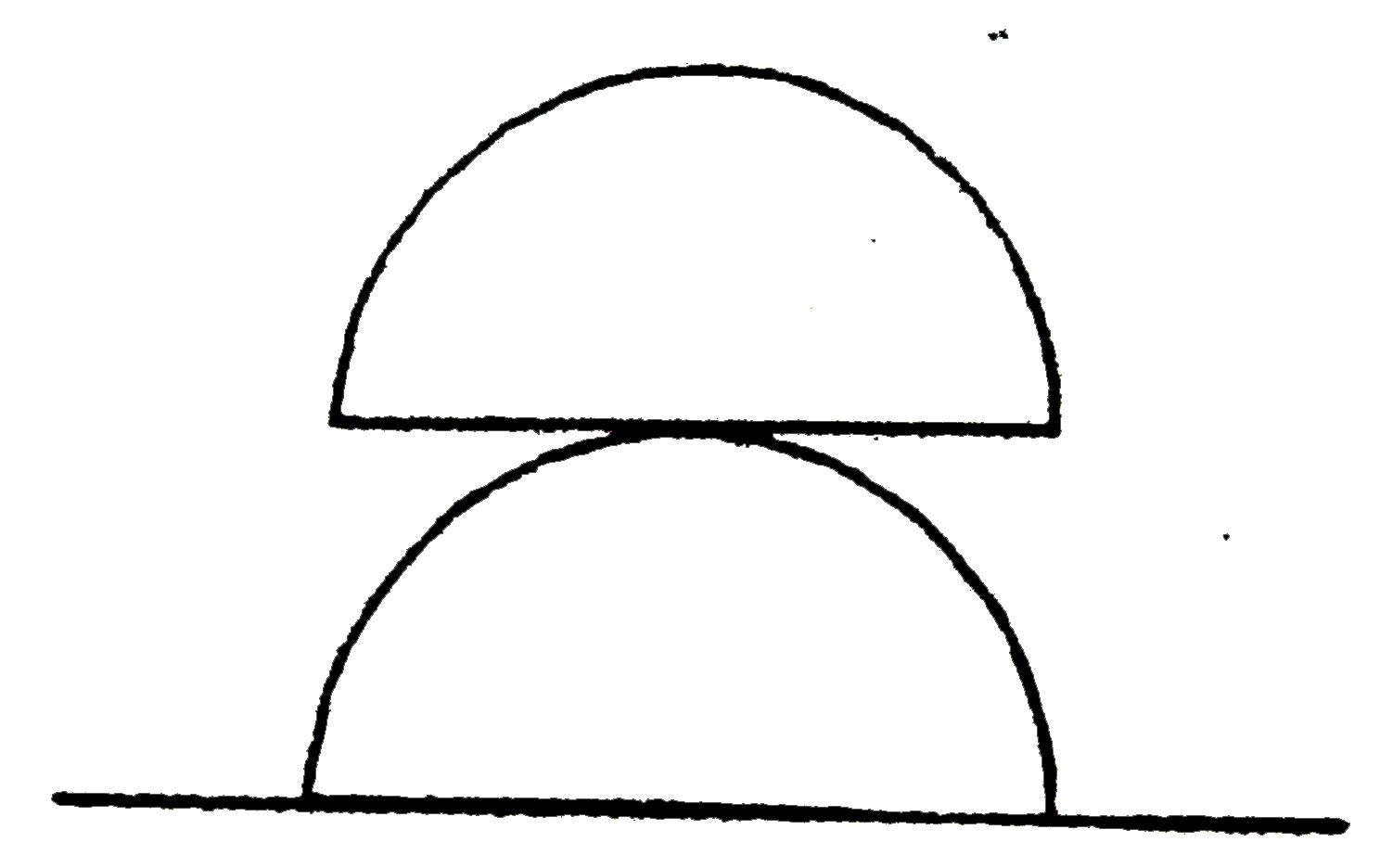
View SolutionA small sphere of mass 1kg is moving with a velocity (6ˆi+ˆj)m/s . It hits a fixed smooth wall and rebounds with velocity (4ˆi+ˆj)m/s. The coefficient of restitution between the sphere and the wall is
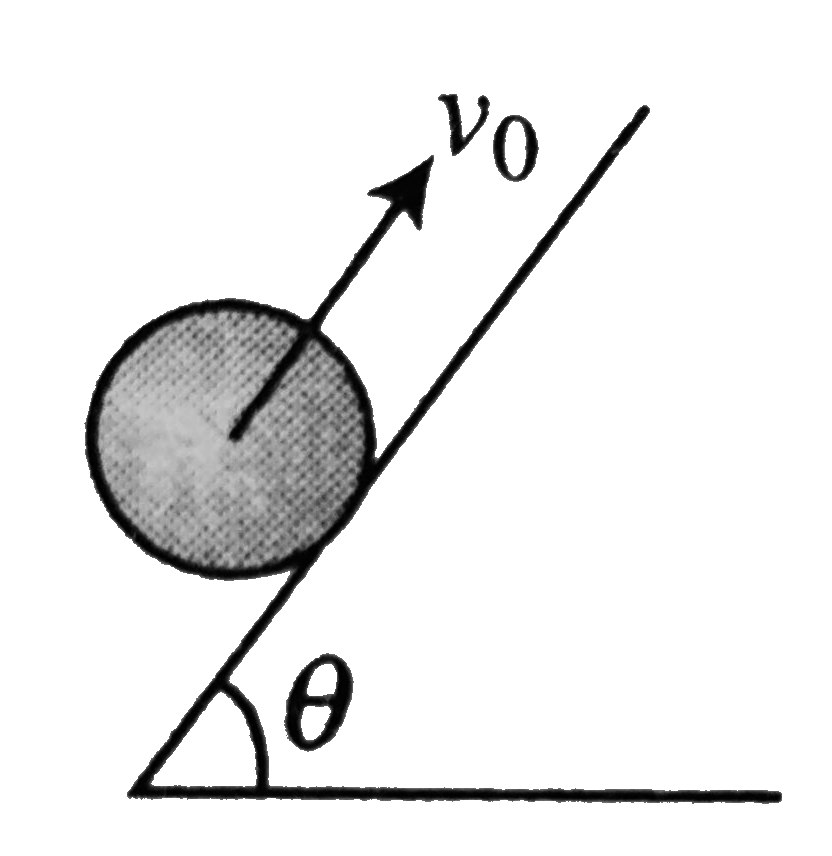
View SolutionA sphere is projected up an inclined plane with a velocity v0 and zero angular velocity as shown. The coefficient of friction between the sphere and the plane is μ=tanθ.. Find the total time of rise of the sphere.
View SolutionA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.
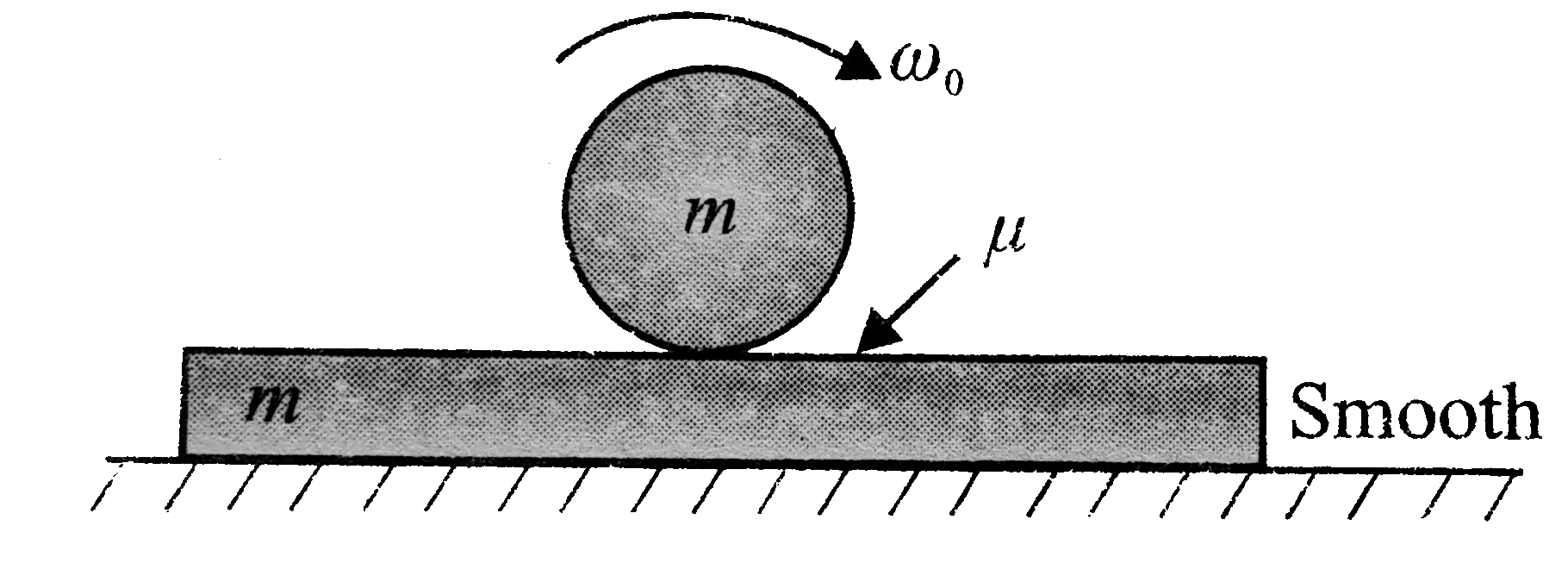
Find the velocity of the sphere after the pure rolling starts
View SolutionA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the displacement of the plank till the sphere starts pure rolling.
View Solution
