A sphere is projected up an inclined plane with a velocity v0 and zero angular velocity as shown. The coefficient of friction between the sphere and the plane is μ=tanθ.. Find the total time of rise of the sphere.
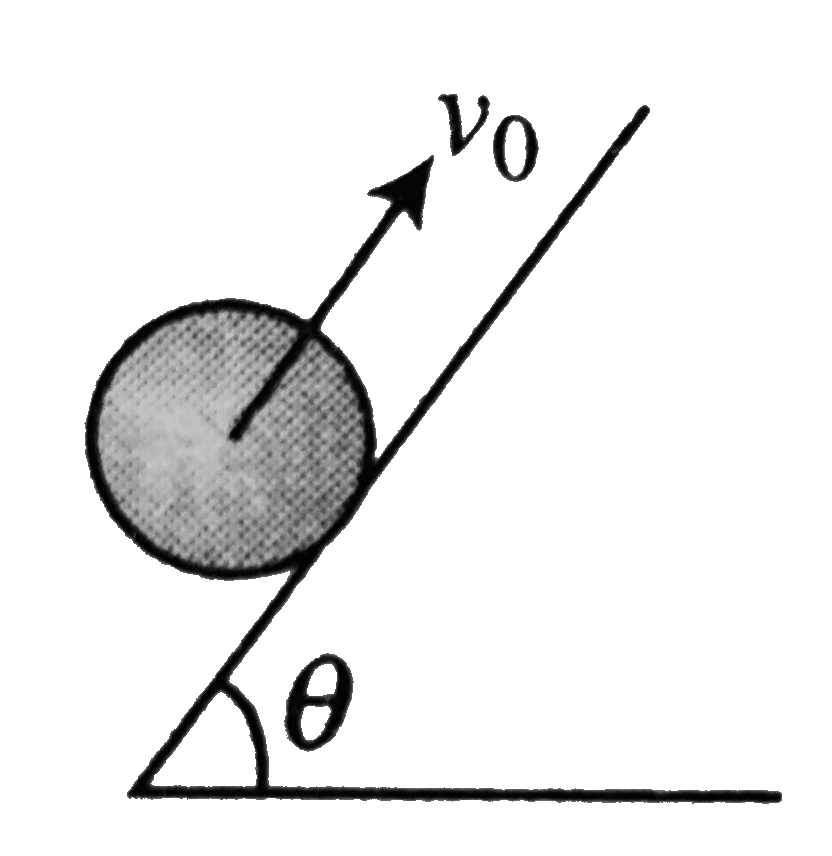
v0gcosθ
v0gsinθ
v0sinθg
none
The correct Answer is:V
The friction will act on the sphere is downward direction before pure rolling starts.

The frictional force is
fk=μN=tanθmgcosθ=mgsinθ
∴ Retardation of sphere a1=mgsinθ+fkm
a1=2gsinθ.i
Now fkr=Icmα
mgsinθR=25mR2α
∴α=5gsinθ2R.............iii
Now let time elapsed before pure rolling starts be t1.
v=wR
v0−2gsinθ1=52gsinθt1
t1=2v09gsinθ.........iii
Once the pure rolling starts, retardation of sphere is
a2=gsinθmR2
also velocity of sphere when pure rolling starts
v=v0−2gsinθt1=v0−4v09=5v09........iv
Now let time elapsed for further rise till stops be t2
∴v−a2t2≡0⇒5v09−57gsinθt2=0
∴t2=7v09gsinθ ................v
∴ Total time to rise t=t1+t2
=2v09gsintη+7v09gsinθ=v0gsinθ
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Single Correct142videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct26videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.413videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
The coefficient of friction between the block and the inclined plane is μ.
View SolutionA block of mass m is projected up with a velocity v0 along an inclined plane of angle of inclination θ=37∘. The coefficient of friction between the inclined plane AB and blocks is μ(=tanθ). Find the values of v0 so that the block moves in a circular path from B to C.
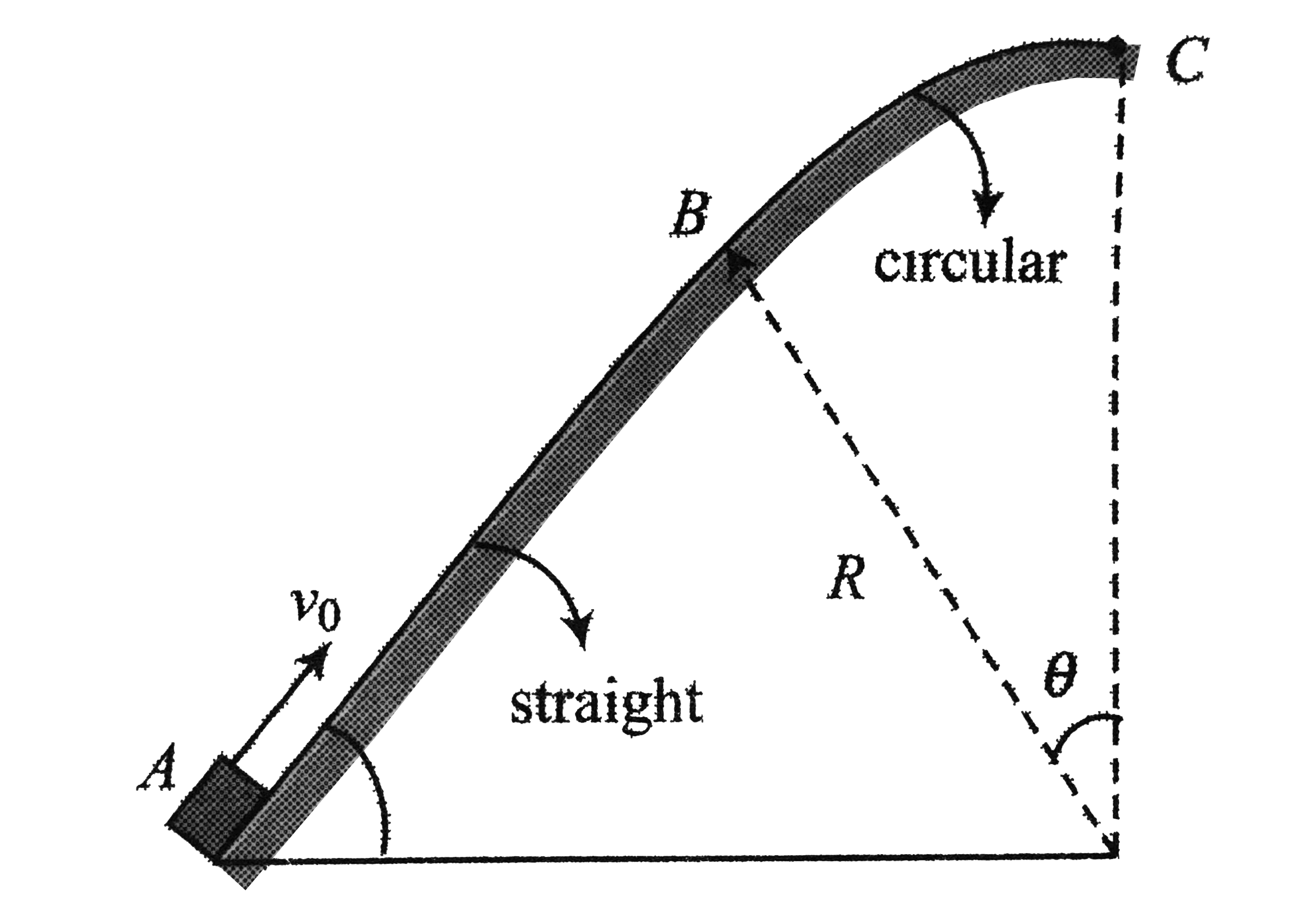 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A block is stationary on an inclined plane If the coefficient of friction between the block and the plane is μ then
 .Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θ
.Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θ - Question 2 - Select One
A long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the velocity of the sphere after the pure rolling startsA2ω0r9Bω0r9Cω0r3D2ω0r3 - Question 3 - Select One
A block of mass m slides down a rough inclined plane of inclination θ with horizontal with zero initial velocity. The coefficient of friction between the block and the plane is μ with θ>tan−1(μ). Rate of work done by the force of friction at time t is
Aμmg2tsinθBmg2t(sinθ−μcosθ)Cμmg2tcosθ(sinθ−μcosθ)Dμmg2tcosθ
A paricle is projected up from the bottom of an inlined plane of inclination α with velocity v0 If it returns to the points of projection after an elastic impact with the plane, find the total time of motion of the particle.
View SolutionA uniform solid sphere of radius r is rolling on a smooth horizontal surface with velocity V and angular velocity ω=(V=ωr). The sphere collides with a sharp edge on the wall as shown in Fig. The coefficient of friction between the sphere and the edge μ=1/5. Just after the collision the angular velocity of the sphere becomes equal to zero. The linear velocity of the sphere just after the collision is equal to
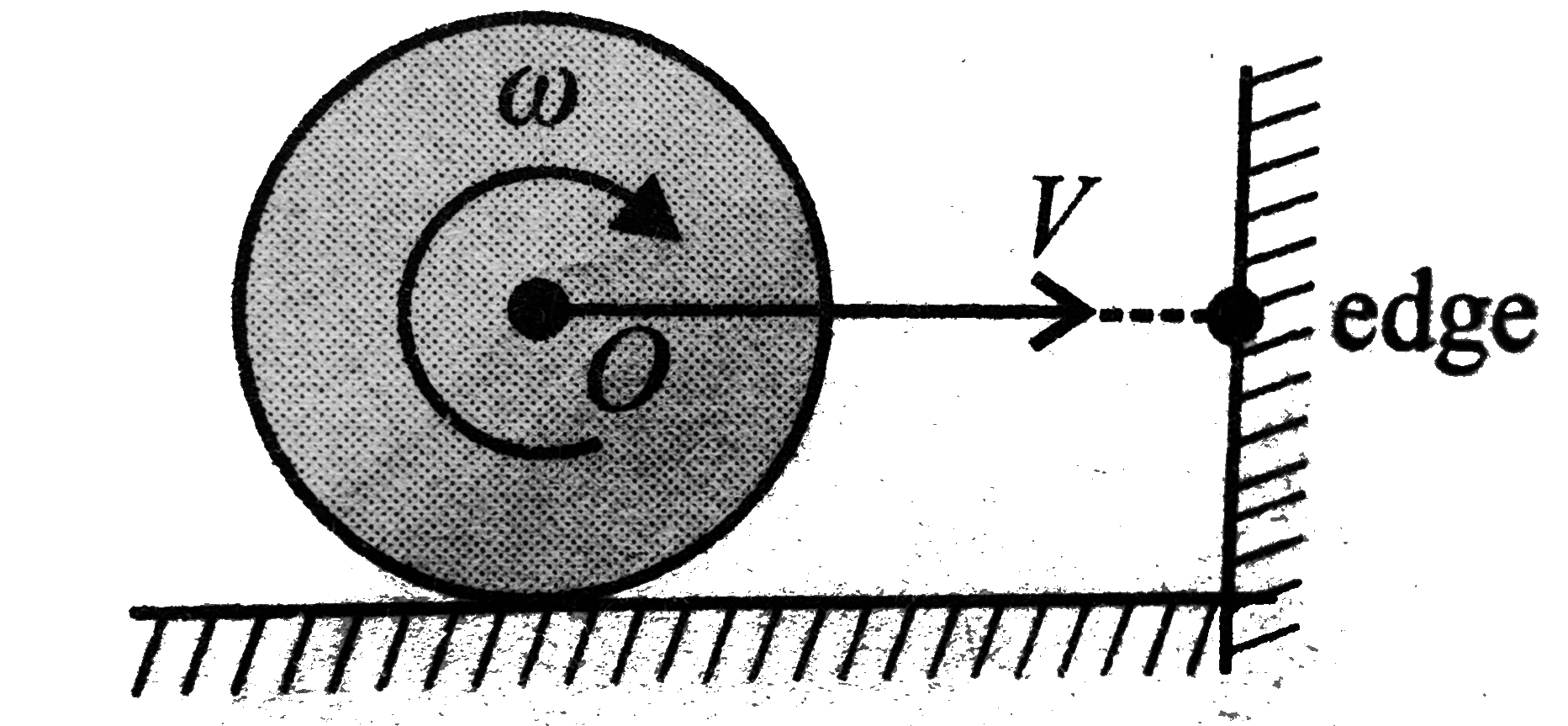 View Solution
View SolutionA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the velocity of the sphere after the pure rolling startsView SolutionA uniform solid sphere of radius r is rolling on a smooth horizontal surface with velocity v and angular velocity ω=(v=ωr). The sphere collides with a sharp edge on the wall as shown in figure. The coefficient of friction between the sphere and the edge μ=1/5. Just after the collision the angular velocity of the sphere becomes equal to zero. The linear velocity of the surface just after the collision is equal to
 View Solution
View SolutionA body is projected up along a rough inclined plane of inclination 45∘ . The coefficient of friction is 0.5. Then the retardation of the block is
View Solution

