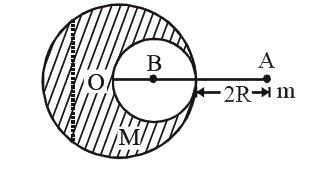
A solid sphere of uniform density and radius R applies a gravitational force of attraction equal to F1 on a particle placed at P, distance 2R from the centre O of the sphere. A spherical cavity of radius R/2 is now made in the sphere as shown in figure. The particle with cavity now applies a gravitational force F2 on same particle placed at P. The radio F2/F1 will be
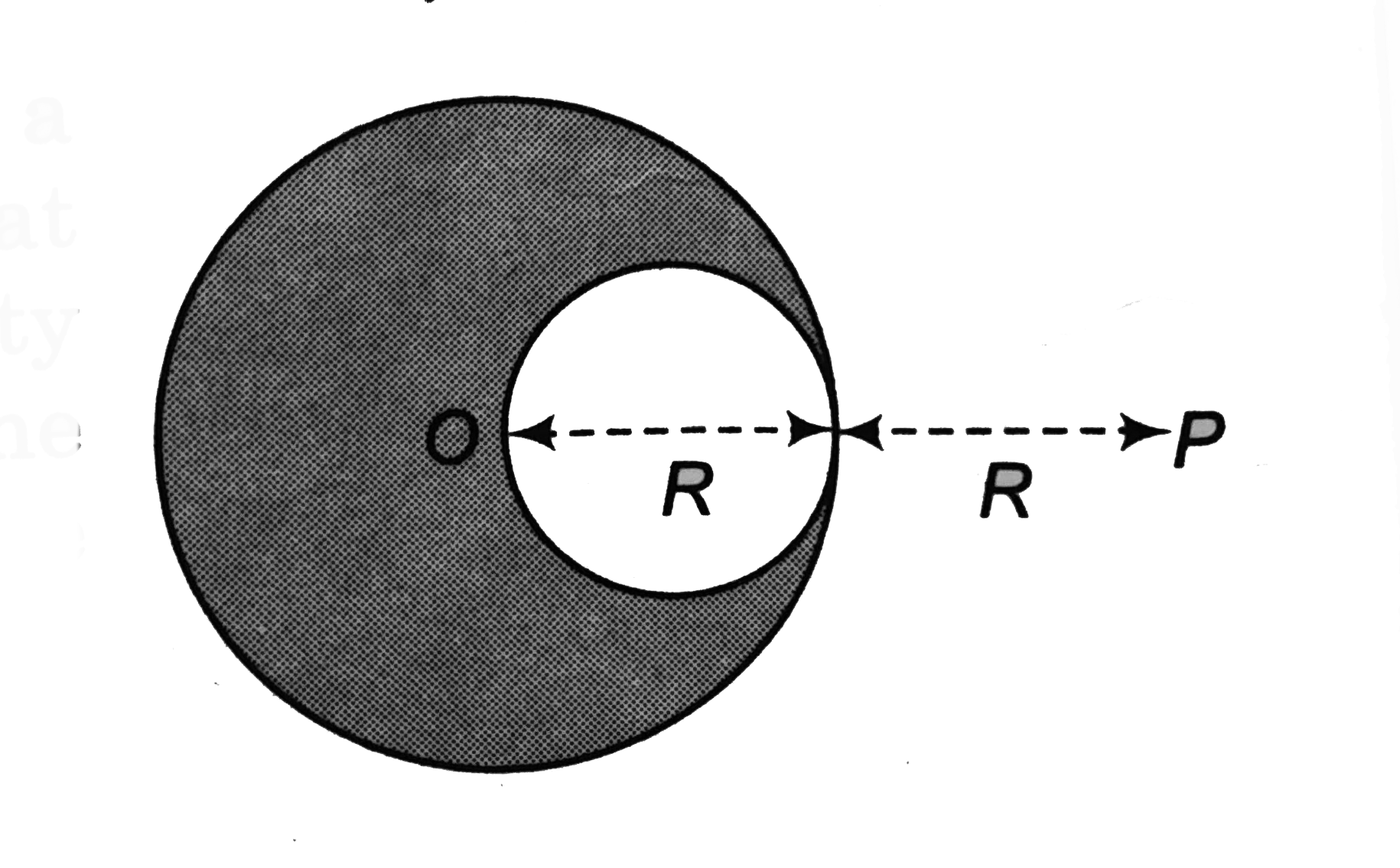
If M and m are the masses of solid sphere and particle respectively and R is the radius of the sphere, then gravitational force of attraction acting on the particle at P is, F1=GMm/4R2.
Mass of sphere of radius R/2=43π(R/2)3ρ=M8
The gravitational force of attraction (F2) acting on the particle due to sphere with cavity = force due to soild sphere - force due to the sphere creating the cavity assumed to be present at that position alone
So, F2=GMm(2R)2−G(M/8)m(3R/2)2=736GMmR2
Hence, F2F1=736GMmR2(GMm4R2)=79
Topper's Solved these Questions
- GRAVIATIONBook:PRADEEPChapter:GRAVIATIONExercise:VALUE BASED QUESTIONS
Explore 5 Videos
- GRAVIATIONBook:PRADEEPChapter:GRAVIATIONExercise:CURIOSITY QUESTION
Explore 1 Video
- GRAVIATIONBook:PRADEEPChapter:GRAVIATIONExercise:VERY SHORT ANSWER QUESTIONS
Explore 11 Videos
- BEHAVIOUR OF PERFECT GAS & KINETIC THEORYBook:PRADEEPChapter:BEHAVIOUR OF PERFECT GAS & KINETIC THEORYExercise:Assertion - Reason Type questions
Explore 14 Videos
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:1 NCERT Comprehension
Explore 4 Videos
Similar Questions
A solid sphere of uniform density and radius R applies a gravitational force of attraction equal to F1 on a particle placed at a distance 3R from the center of the sphere. The 1 sphere with the cavity now applies a gravitational force F2, on the same particle. Then ratio F1F2 is
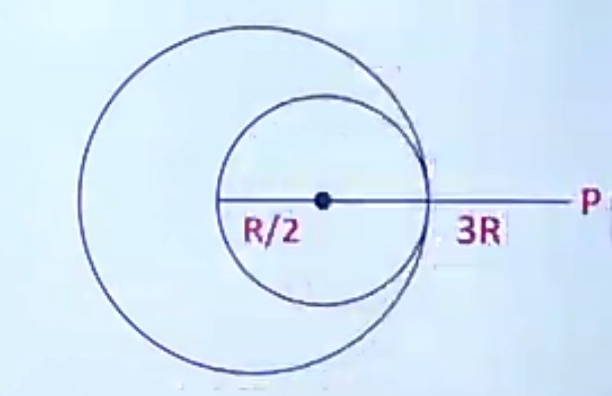
View SolutionThe gravitational force acting on a particle, due to a solid sphere of uniform density and radius R, at a distance of 3R from the centre of the sphere is F1. A spherical hole of radius (R/2) is now made in the sphere as shown in diagram. The sphere with hole now exerts a force F2 on the same particle. ratio of F1 to F2 is
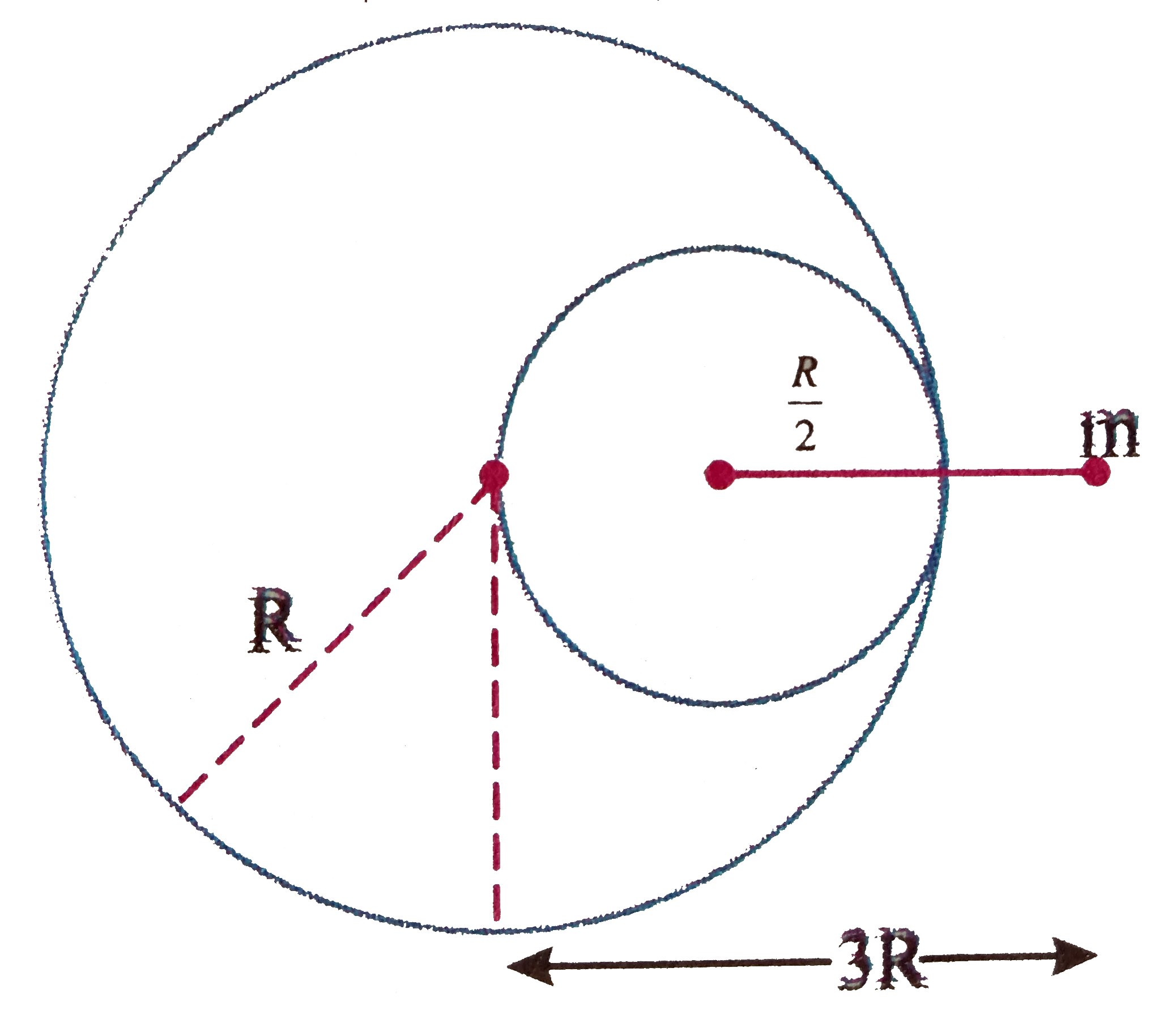
View Solution
Knowledge Check
A solid sphere of uniform density and radius R applies a gravitational force attraction equal to F1 on a particle placed at P, distance 2R from the centre O of the sphere. A spherical cavity of radius R/2 is now made in the sphere as shows in figure. The particle with cavity now applies a gravitational force F2 on same particle placed at P. The radio F2/F1 will be
 A1/2B7/9C3D7
A1/2B7/9C3D7A solid sphere of uniform density and radius R applies a gravitational force of attraction equal to F1 on a particle placed at P, distance 2R from the centre O of the sphere. A spherical cavity of radius R/2 is now made in the sphere as shown in given figure. The sphere with cavity now applies a gravitational force F2 on same particle placed at P. The ratio F2/F1 will be
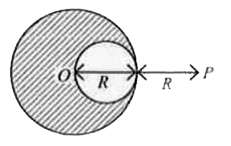 A1/2B7/9C3D7
A1/2B7/9C3D7A solid sphere of uniform density and radius R applies a gravitational force of attraction equal to F1 on a particle placed at P, distance 2R from the centre O of the sphere. A spherical cavity of radius R/2 is now made in the sphere as shown in figure. The particle with cavity now applies a gravitational force F2 on same particle placed at P. The radio F2/F1 will be
 A12B79C3D7
A12B79C3D7
A solid of radius 'R' is uniformly charged with charge density ρ in its volume. A spherical cavity of radius R2 is made in the sphere as shown in the figure. Find the electric potential at the centre of the sphere.

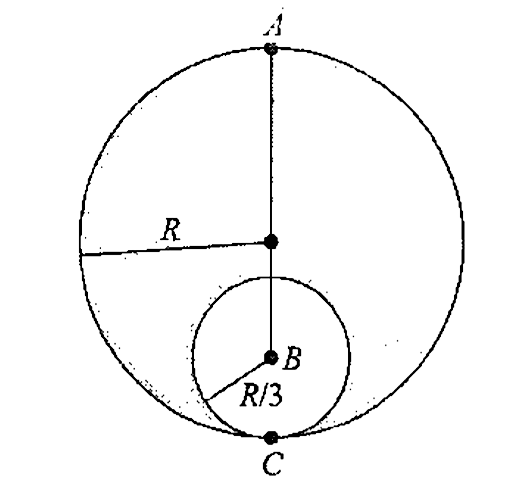
View SolutionInside a uniform sphere of mass M and radius R, a cavity of radius R/3, is made in the sphere as shown :
View SolutionA solid sphere of radius R gravitationally attracts a particle placed at 3R form its centre with a force F1. Now a spherical cavity of radius (R2) is made in the sphere (as shown in figure) and the force becomes F2 The value of F1:F2 is:
View SolutionA hemi-spherical cavity is created in solid sphere (of radius 2R) as shown in the figure. Then

View SolutionA hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . Then y -coordinate of the centre of mass of the remaining sphere is

View Solution