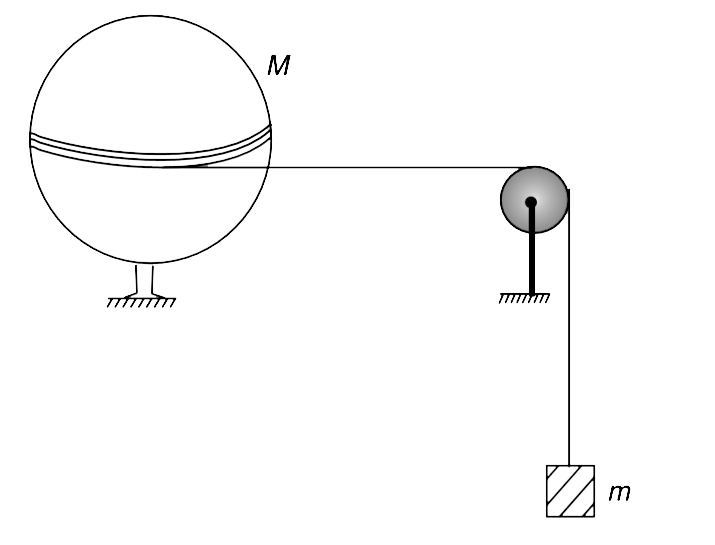
A solid uniform sphere of mass M and radius R can rotate about a fixed vertical axis. There is no frictional torque acting at the axis of rotation. A light string is wrapped around the equator of the sphere. The string has exactly 6 turns on the sphere. The string passes over a light pulley and carries a small mass m at its end (see figure). The string between the sphere and the pulley is always horizontal. The system is released from rest and the small mass falls down vertically. The string does not slip on the sphere till 5 turns get unwound. As soon as turn gets unwound completely, the friction between the sphere and the string vanishes all of a sudden.
(a) Find the angular speed of the sphere as the string leaves it.
(b) Find the change in acceleration of the small mass after 5 turns get unwound from the sphere.
The correct Answer is:(a)
(b)
Step by step video, text & image solution for A solid uniform sphere of mass M and radius R can rotate about a fixed vertical axis. There is no frictional torque acting at the axis of rotation. A light string is wrapped around the equator of the sphere. The string has exactly 6 turns on the sphere. The string passes over a light pulley and carries a small mass m at its end (see figure). The string between the sphere and the pulley is always horizontal. The system is released from rest and the small mass falls down vertically. The string does not slip on the sphere till 5 turns get unwound. As soon as 5^(th) turn gets unwound completely, the friction between the sphere and the string vanishes all of a sudden. (a) Find the angular speed of the sphere as the string leaves it. (b) Find the change in acceleration of the small mass m after 5 turns get unwound from the sphere. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
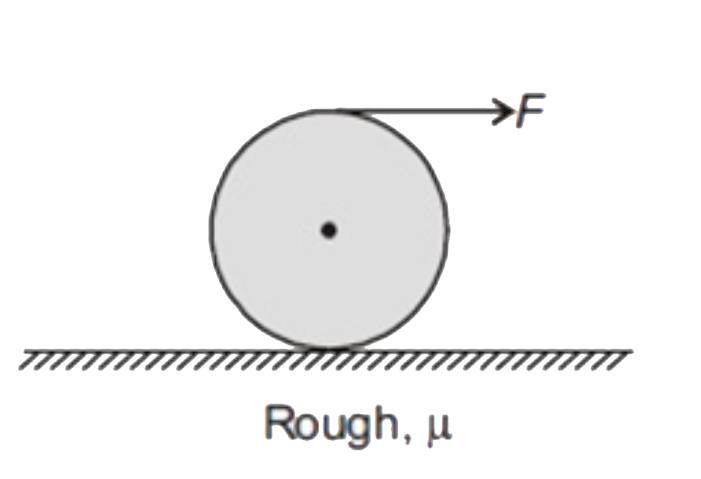
A solid sphere of mass M and radius R is pulled by a force F as shown in figure . If the sphere does not slip over the surface , then frictional force acting on the sphere is
View SolutionA solid sphere of radius r and mass m rotates about an axis passing through its centre with angular velocity ω. Its K.E. Is
View Solution
Knowledge Check
A uniform disc of mass M and radius R is mounted on a fixed horizontal axis. A block of mass m hangs from a massless string that is wrapped around the rim of the disc. The magnitude of the acceleration of the falling block (m) is
A2MM+2mgB2mM+2mgCM+2m2MgD2M+m2MgA solid sphere of mass M and radius R spins about an axis passing through its centre making 600 r.p.m. What is its kinetic energy of rotation?
A25πM2R2B80π2MR2C80πRD25π2MRA solid sphere of mass M and radius R spins about an axis passing through its centre making 600 rpm. Its kinetic energy of rotation is
A25π2MRB25πM2R2C80πMRD80π2MR2
A light string passing over a light smooth pulley carries masses of 3 kg and 5 kg at its ends. If the string is allowed to move from the rest, the acceleration of the motion is equal to :
View SolutionA light string passing over a light smooth pulley carries masses of 3 kg and 5 kg at its ends. If the string is allowed to move from the rest, the acceleration of the motion is equal to :
View SolutionA uniform disc of mass M, radius R is attached to a frictionless horizontal axis. Its rim is wound with a light string and a tension T is applied to it, the angular acceleration will be?
View SolutionTwo masses M and m(M>m) are joined by a light string passing over a smooth light pulley.
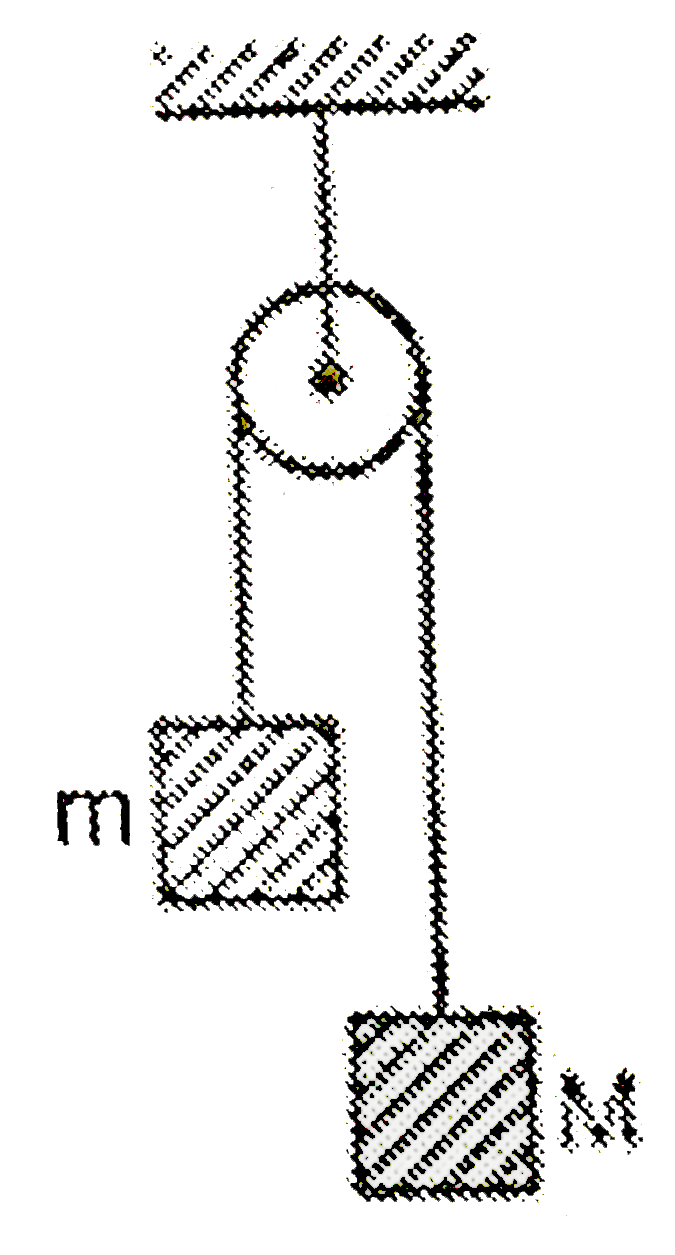
View SolutionA solid sphere of mass m and radius R is rotating about its diameter. A solid cylinder of the same mass and same radius is also rotating about its geometrical axis with an angular speed twice that of the sphere. The ratio of their kinetic energies of rotation (Esphere/Ecylinder) will be
View Solution
