A solid uniform sphere rotating about its axis with kinetic energy $E_{1}$ is gently placed on a rough horizontal plane at time t=0, Assume that, at time $t = t_{1}$ , it starts pure rolling and at that instant total KE of the sphere is $E_{2} .$ After sometime, at time $t = t_{2}$ . KE of the sphere is $E_{3}$ . Then

$E_{1} = E_{2} = E_{3}$

$E_{1} > E_{2} = E_{3}$

$E_{1} > E_{2} > E_{3}$

$E_{1} < E_{2} = E_{3}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Answer

Step by step video, text & image solution for A solid uniform sphere rotating about its axis with kinetic energy E_(1) is gently placed on a rough horizontal plane at time t=0, Assume that, at time t=t_(1), it starts pure rolling and at that instant total KE of the sphere is E_(2). After sometime, at time t=t_(2). KE of the sphere is E_(3). Then by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
A sphere is rolling on a horizontal surface without slipping. The ratio of the rotational K.E. to the total kinetic energy of the sphere is
A $\frac{2}{5}$
B $\frac{2}{7}$
C $\frac{5}{7}$
D $\frac{3}{7}$
Question 2 - Select One
A long horizontal plank of mass $m$ is lying on a smooth horizontal surface. A sphere of same mass $m$ and radius $r$ is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is $μ$ . After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the displacement of the plank till the sphere starts pure rolling.
A $\frac{ω_{0}^{2} r^{2}}{81 μ g}$
B $\frac{2}{27} \frac{ω_{0}^{2} r^{2}}{μ g}$
C $\frac{4}{81} \frac{ω_{0}^{2} r^{2}}{μ g}$
D $\frac{2}{81} \frac{ω_{0}^{2} r^{2}}{81 μ g}$
Question 3 - Select One
A long horizontal plank of mass $m$ is lying on a smooth horizontal surface. A sphere of same mass $m$ and radius $r$ is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is $μ$ . After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

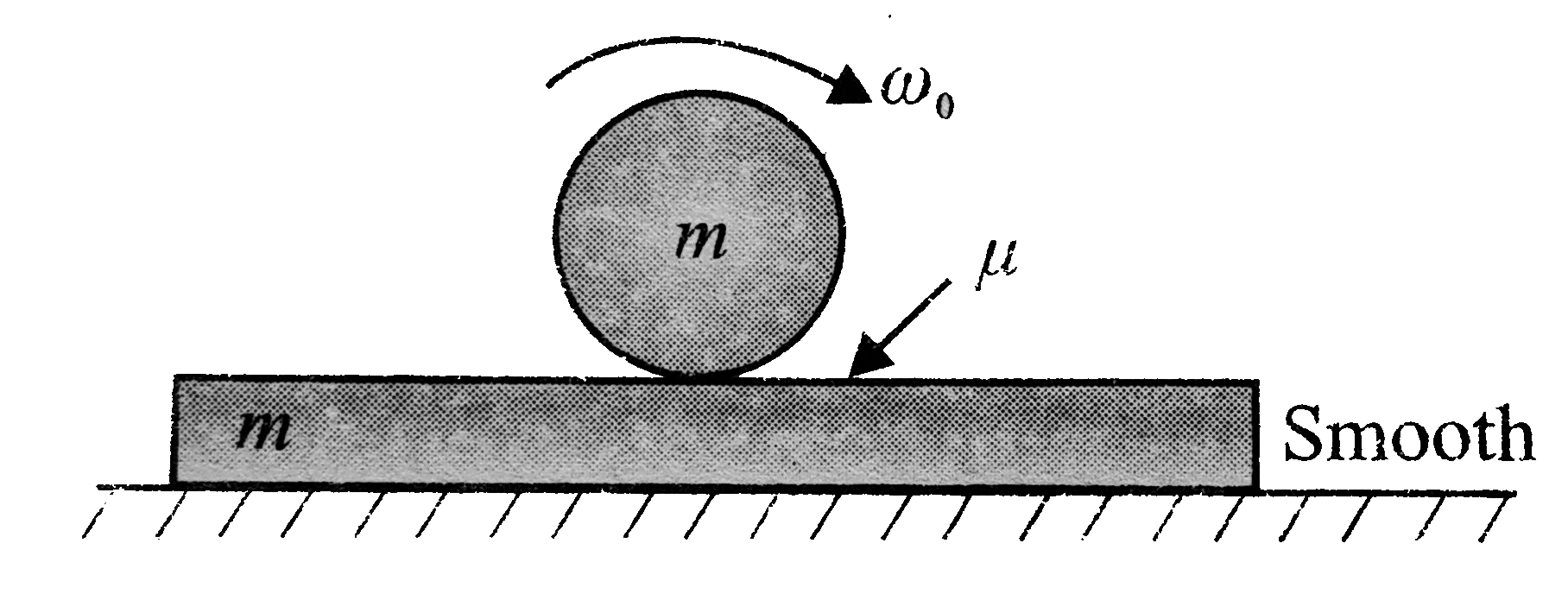
Find the time $t$ at which the pure roiling starts
A $\frac{ω_{0} r}{9 μ g}$
B $\frac{2 ω_{0} r}{9 μ g}$
C $\frac{ω_{0} r}{3 μ g}$
D $\frac{2 ω_{0} r}{μ g}$