A source of acoustic wave of the frequency and a receiver are located at the same point. At the instant , the source start from rest to move away from the receiver with a constant acceleration . The velocity of sound in air is .
If for 10s and then for , the apparent frequency recorded by the receiver at
The correct Answer is:B
Source frequency . Source (coinciding with observer at ) moves away with uniform acceleration . Consider the wave which is received by the observer at instant It will have left the source at an earlier instant of time, say , when the distance of source was r(say). If u be velocity of source at instant t, then and . We then have the relation between and
This is quadratic equation in t, giving the solution
Then apparent frequency is given by
Putting values ,,,
We have
Topper's Solved these Questions
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Assertion-Reasoning
24 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Comprehension Type
5 Videos
Similar Questions
A source S of acoustic wave of the frequency v0=1700Hz and a receiver R are located at the same point. At the instant t=0, the source start from rest to move away from the receiver with a constant acceleration ω. The velocity of sound in air is v=340ms.
Q. If ω=10ms2, the apparent frequency that will be recorded by the stationary receiver at t=10s will be
View SolutionA source of sonic oscillations with frequency n=1700Hz and a receiver are located on the same normal to a wall. Both the source and receiver are stationary, and the wall recedes from the source with velocity u=6.0ms. Find the beat frequency registered by the receiver. The velocity of sound is v=340ms.
View SolutionA source of sonic oscillations with frequency n=1700Hz and a receiver are located on the same normal to a wall. Both the source and receiver are stationary, and the wall recedes from the source with velocity u=6.0ms. Find the beat frequency registered by the receiver. The velocity of sound is v=340ms.
View SolutionA listener is at rest and a police siren is moving away from the listerner at 60m/s. what frequency does the listerner hear given that the velocity of sound in air is 340m/s and frequency os siren is 500Hz?
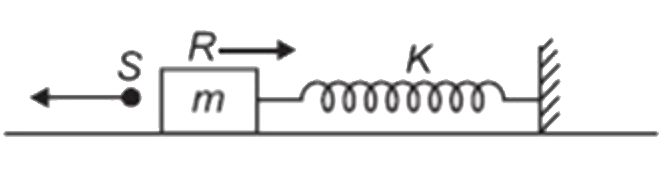
View SolutionA sound source S, emitting a sound of frequency 400 Hz and a receiver R of mass m are at the same point. R is performing SHM with the help of a spring of force constant K. At a time t = 0, R is at the mean position and moving towards the right, as shown. At the same time, the source starts moving away from R with some acceleration a. The frequency registered by the receiver at a time t = 10 s is 250 Hz. What is the time (in seconds) at which the corresponding registered frequency of 250 Hz was emitted by the source? [Given that mK=25π2 and amplitude of oscillation = 100πm,Vsound = 320 m s^(-1)]
View SolutionA source of sound of frequency 300 Hz and a receiver are located along the same line normal to the wall as shown in the figure. Both the source and the receiver are stationary and the wall receeds from the source with velocity 20ms−1.If the beat frequency registered by the receiver is 240x Hz then x is :
(Assume Vsound=300 m/s).

View SolutionA car is moving with a constant velocity 10m/s towards the stationary wall. The car blows a horn of frequency 320Hz. The velocity of sound in air is 330m/s. The beats frequency received by the observer is

View Solution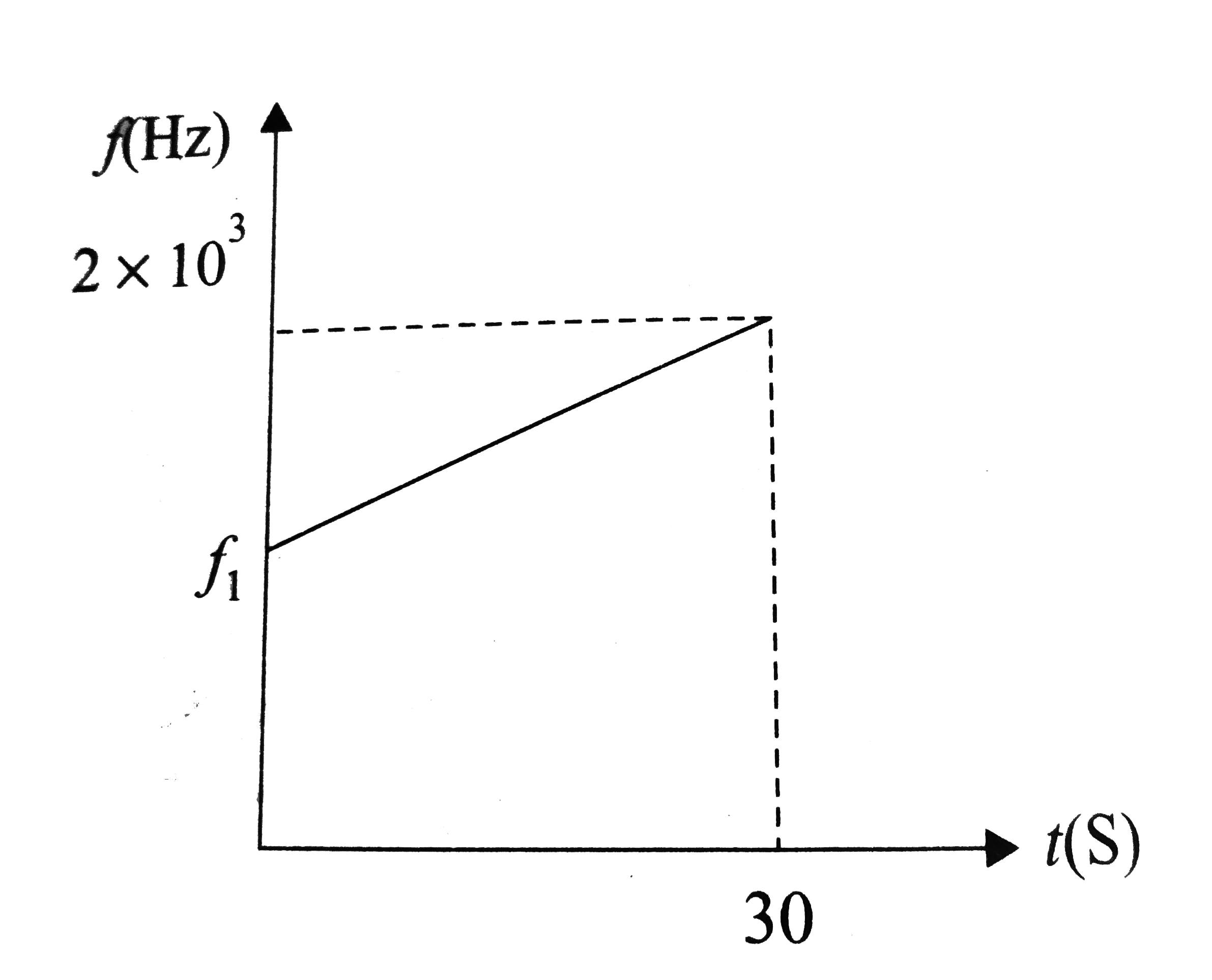
A source of sound of frequency f1 is placed on the ground. A detector placed at a height is released from rest on this source. The observed frequency f(Hz) is plotted against time t(sec) . The speed of sound in air is 300ms. Find f1 (g=10ms).
View Solution
A source of sound of frequency f1 is placed on the ground. A detector placed at a height is released from rest on this source. The observed frequency f(Hz) is plotted against time t(sec) . The speed of sound in air is 300ms. Find f1 (g=10ms).
View Solution
A source of sound of frequency f1 is placed on the ground. A detector placed at a height is released from rest on this source. The observed frequency f(Hz) is plotted against time t(sec) . The speed of sound in air is 300ms. Find f1 (g=10ms).
View Solution
