A spaceship approaches the Moon (mass and radius along a parabolic path which is almost tangential to its surface. At the moment of the maximum approach, the brake rocket is fired to convert the spaceship into a satellite of the Moon. Find the change in speed.
The correct Answer is:
If the velocity at the vertex of the parabola, then is also the escape velocity. It will follow the parabolic path ever to return to the Moon. Now
The negaive sign means the speed has to be decreased.
Therefore, the required change in the speed is
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Single Correct122videos
GRAVITATION
- BOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Multiple Correct24videos
GRAVITATION
- BOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Exercise 6.416videos
GRAVITATION
- BOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE1videos
FLUID MECHANICS
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer9videos
KINEMATICS-1
Similar Questions
A spaceship approaches the Moon along a parabolic trajectory which is almost tangent to the Moon's surface. At the moment of the maximum approach the brake rocket was fired for a short time interval, and the spaceship was transferred into a circular orbit of a Moon satellic. Find how the spaceship velocity modulus increased in the process of braking.
View SolutionA sapceship nears the Moon along a parabolic trajectory that almost toches the Moon's surface. In order to transfer closest approach. The engine ejects gas ata speed of u=4km/s realtive to the spaceship In its direction of motion. If v1= velocity of spaceship in parabolic trajectory, when it almost touches the earth and v2= velocity of spaceship in circular orbit when it almost to'uches the earth. Then what friction of total mass should the fuel burn to transfer space ship to circular orbit?
View Solution
Knowledge Check
- Question 1 - Select One
The moment of inertia of a disc of mass M and radius R about an axis. Which is tangential to sircumference of disc and parallel to its diameter is.
A54MR2B23MR2C32MR2DMR2 - Question 2 - Select One
A satellite of mass m revolves around the earth of radius R at a hight x from its surface. If g is the acceleration due to gravity on the surface of the earth, the orbital speed of the satellite is
AgR2R+xBgRR−xCgxD(gR2R+x)1/2 - Question 3 - Select One
_E01_028_Q01.png)
Spacemen Fred's spaceship (which has negligible mass) is in an elliptical orbit about planet Bob. The minimum distance between the spaceship and the planet is R, the maximum distance between the spaceship and the planet is 2R. At the point of maximum distance, spaceman fred is traveling at speed v0. he then fires his thrusters so that he enters a circular orbit of radius 2R. what is his new speed?A√3/2v0B√5v0C√3/56v0D√2v0
A spaceship approaches the Moon along a parabolic trajectory which is almost tangent to the Moon's surface. At the moment of the maximum approach the brake rocket was fired for a short time interval, and the spaceship was transferred into a circular orbit of a Moon satellic. Find how the spaceship velocity modulus increased in the process of braking.
View Solution
A ball of mass m and radius r rolls along a circular path of radius R its speed at the bottom (θ=0∘) of the path is v0 find the force of the path on the ball as a function of θ.View Solution
A small asteroid is approaching a planet of mass M and radius R from a large distance. Initially its velocity (u) is along a tangent to the surface of the planet. It fall on the surface making an angle of 302 with the vertical. Calculate u.View SolutionA hoop with mass M and radius R lies flat on a perfectly smooth surface. An insect with mass m rests on it. On being distrubed by some noise it starts crawling on the hoop with speed v. Find the trajectory of the centre of the hoop and its speed.
View SolutionA spaceship is sent to investigate a planet of mass M and radius R. While hanging motionless in space at a distance 5R from the centre of the planet, the spaceship fires an instrument package of mass m, which is much smaller than the mass of the spaceship. For what angle θ will the package just graze the surface of the planet?
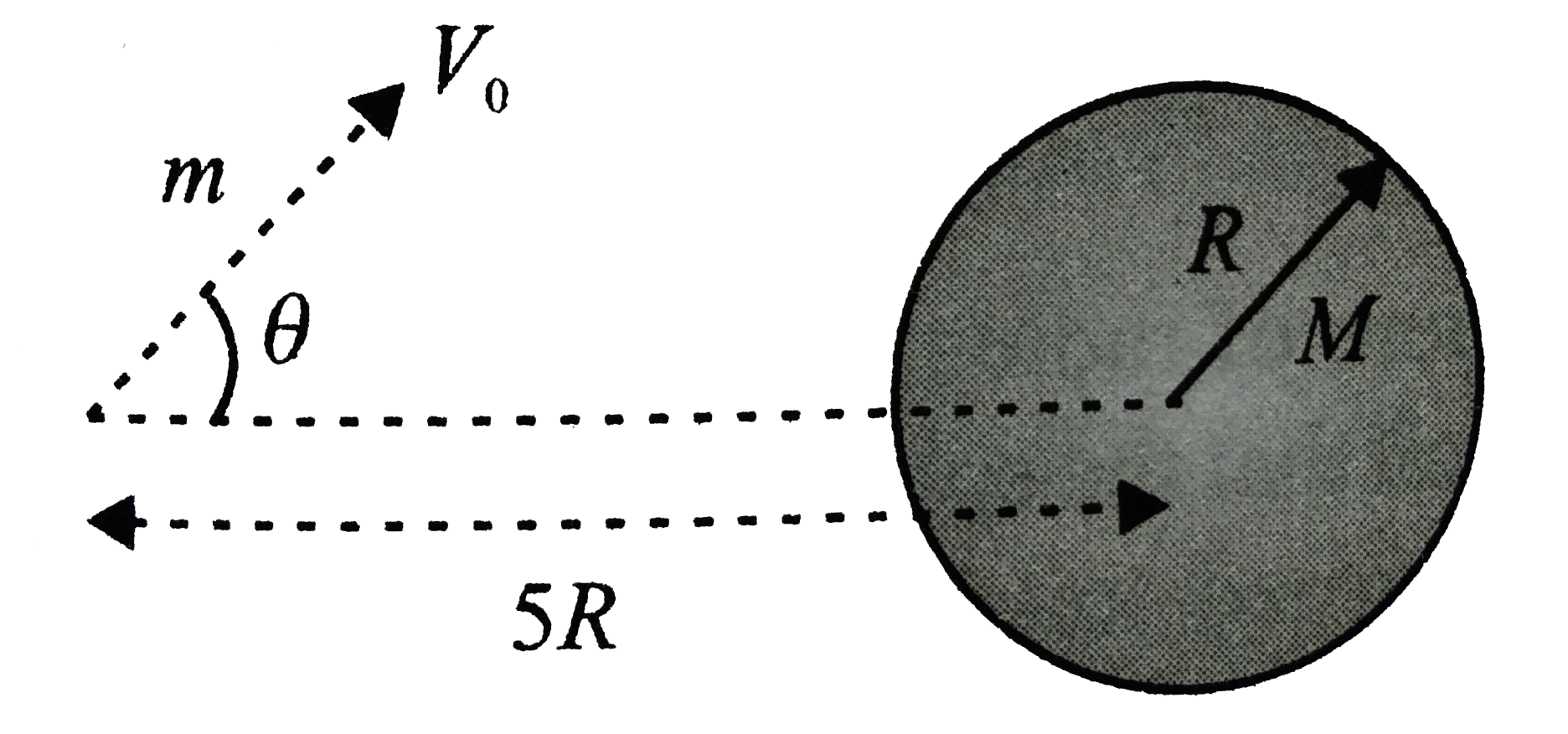View Solution