A sphere is rotating about a diameter
the particles on the surface of the sphere do not have any linear acceleration
the particles on the diameter mentioned above do not have any linear acceleration
different particle son the surfce have different angular speeds.
All particles on the surface have same linear speed
The correct Answer is:B
To solve the problem regarding the rotation of a sphere about its diameter, we will analyze the statements provided in the question step by step.
1. Understanding the Rotation:
A sphere is rotating about its diameter with an angular velocity ω. Each point on the surface of the sphere will have a linear speed that depends on its distance from the axis of rotation.
2. Linear Speed Calculation:
The linear speed v of a point on the surface of the sphere is given by the formula:
v=rω
where r is the distance from the axis of rotation (the diameter in this case) to the point on the surface.
3. Analyzing the First Statement:
The first statement claims that "all particles on the surface have the same linear speed." Since r varies for different points on the surface (e.g., points at the equator have a larger r than points near the poles), the linear speed v will also vary. Therefore, this statement is incorrect.
4. Analyzing the Second Statement:
The second statement claims that "the particles on the diameter mentioned above don't have any linear acceleration." For particles on the diameter (which is the axis of rotation), the distance r from the axis is zero. Thus, their linear speed v is:
v=0⋅ω=0
Since their speed is constant (zero), these particles do not have any linear acceleration. Therefore, this statement is correct.
5. Analyzing the Third Statement:
The third statement claims that "different particles on the surface have different angular speeds." However, all particles on the surface of the sphere share the same angular velocity ω since they complete the rotation in the same time. Thus, this statement is incorrect.
6. Analyzing the Fourth Statement:
The fourth statement claims that "particles on the surface of the sphere don't have any linear acceleration." Since the particles on the surface are moving in a circular path, they experience centripetal acceleration. Therefore, this statement is incorrect.
Summary of Results
- Statement 1: Incorrect
- Statement 2: Correct
- Statement 3: Incorrect
- Statement 4: Incorrect
A sphere is rotating about its diameter with an angular velocity ω. Each point on the surface of the sphere will have a linear speed that depends on its distance from the axis of rotation.
The linear speed v of a point on the surface of the sphere is given by the formula:
v=rω
where r is the distance from the axis of rotation (the diameter in this case) to the point on the surface.
The first statement claims that "all particles on the surface have the same linear speed." Since r varies for different points on the surface (e.g., points at the equator have a larger r than points near the poles), the linear speed v will also vary. Therefore, this statement is incorrect.
The second statement claims that "the particles on the diameter mentioned above don't have any linear acceleration." For particles on the diameter (which is the axis of rotation), the distance r from the axis is zero. Thus, their linear speed v is:
v=0⋅ω=0
Since their speed is constant (zero), these particles do not have any linear acceleration. Therefore, this statement is correct.
The third statement claims that "different particles on the surface have different angular speeds." However, all particles on the surface of the sphere share the same angular velocity ω since they complete the rotation in the same time. Thus, this statement is incorrect.
The fourth statement claims that "particles on the surface of the sphere don't have any linear acceleration." Since the particles on the surface are moving in a circular path, they experience centripetal acceleration. Therefore, this statement is incorrect.
- Statement 1: Incorrect
- Statement 2: Correct
- Statement 3: Incorrect
- Statement 4: Incorrect
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
21 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -1
26 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer
13 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer
15 Videos
Similar Questions
A solid sphere is rotating about a diameter at an angular velocity ω. If it cools so that its radius reduces to 1/n of its original value, its angular velocity becomes
View SolutionSTATEMENT-1 : When a sphere rotates about a diameter, the particles on the surface of sphere have different linear speeds.
STATEMENT-2 : When a ring rotates about its own axis, the particles on the circumference of ring have different linear velocities.
STATEMENT-3 : Linear acceleration of all the particles lying on the surface of a sphere rotating uniformly about its diameter are equal.
View Solution
Knowledge Check
A solid sphere of mass m and radius R is rotating about its diameter. A solid cylinder of the same mass and same radius is also rotating about its geometrical axis with an angular speed twice that of the sphere. The ratio of their kinetic emergies of rotation (Esphere/Ecylinder) will be.
A1:4B3:1C2:3D1:5
A solid sphere is rotating about an axis as shown in figure. An insect follows the dotted path on the cricumference of sphere as shown .
Match the following

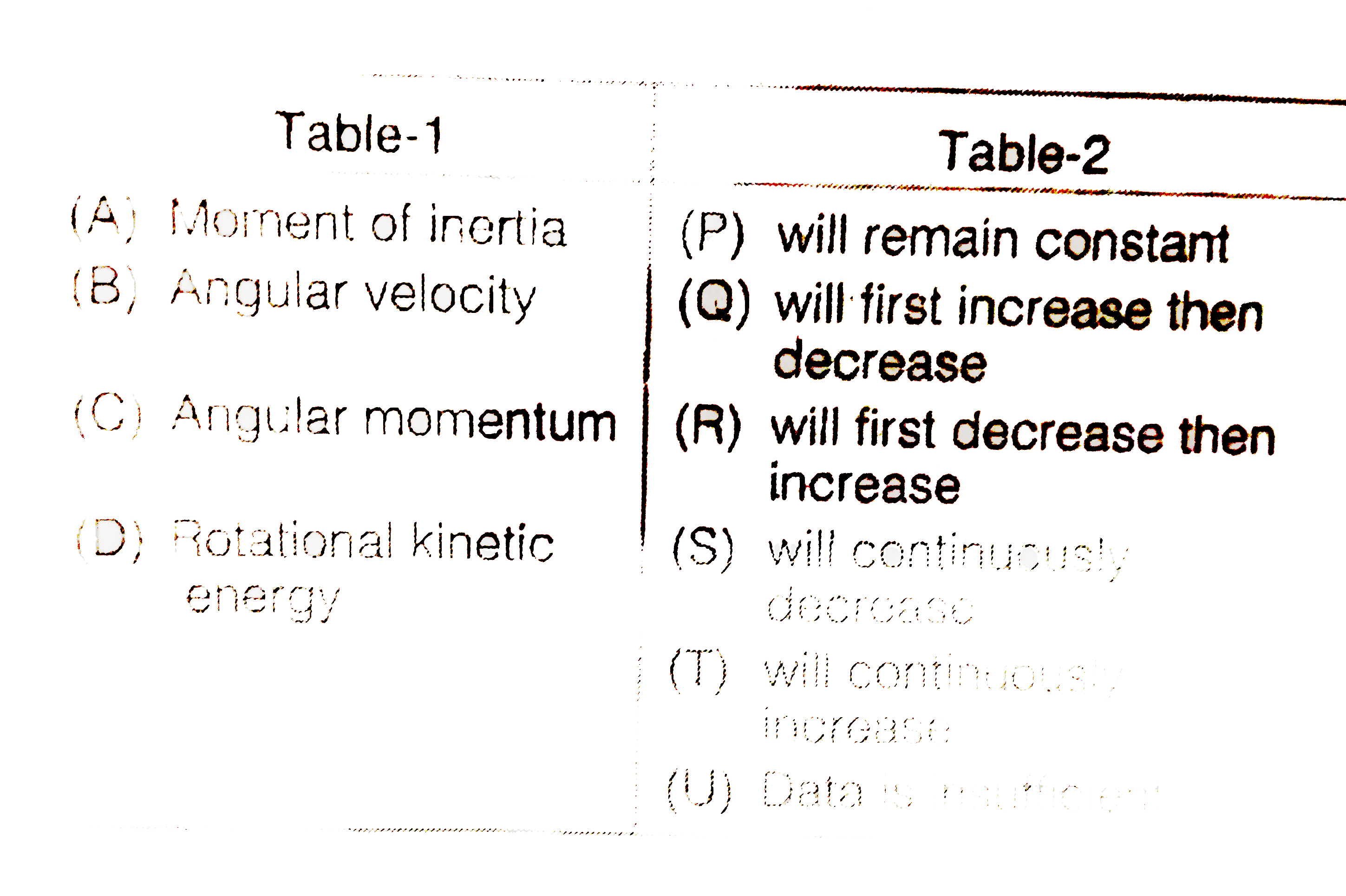
View SolutionA solid sphere of mass m and radius R is rotating about its diameter. A solid cylinder of the same mass and same radius is also rotating about its geometrical axis with an angular speed twice that of the sphere. The ratio of their kinetic emergies of rotation (Esphere/Ecylinder) will be.
View SolutionA uniformly charged solid sphere a mass M, radius R having charge Q is rotated about its diameter with frequency f0. The magnetic moment of the sphere is
View SolutionA hollow sphere of mass 1 kg and radius 10 cm is free to rotate about its diameter. If a force of 30 N is applied tangentially to it, its angular acceleration is (in rad/s2)
View SolutionThe moment of inertia of a solid sphere of radius R about its diameter is same as that of a disc of radius 2R about its diameter. The ratio of their masses is
View SolutionA solid sphere is rotating with a constant angular velocity about an axis touching the surface. Its angular momentum will be:
View SolutionA semi-circle of radius 17.5 cm is rotated about its diameter. Find the curved surface of so generated solid.
View Solution