Let IA and IB be moments of inertia of a body about two axes A and B respectively. The axis A passes through the centre of mass of the body but B does not. Then
IA<IB
IfIA<IB the axes pareparallel
Iftheaxesareparal≤lIA<IB
Iftheaxesare¬paral≤lIA≥IB
The correct Answer is:C
To solve the problem regarding the moments of inertia IA and IB about two different axes A and B, we can follow these steps:
Step 1: Understand the Concept of Moment of Inertia
The moment of inertia of a body is a measure of how difficult it is to change its rotational motion about a given axis. It depends on the mass distribution of the body relative to the axis of rotation.
Step 2: Identify the Axes
- Axis A passes through the center of mass (CM) of the body.
- Axis B does not pass through the center of mass.
Step 3: Apply the Parallel Axis Theorem
The Parallel Axis Theorem states that if you know the moment of inertia ICM about an axis through the center of mass, you can find the moment of inertia about any parallel axis using the formula:
IB=ICM+Md2
where:
- IB is the moment of inertia about axis B,
- ICM is the moment of inertia about the center of mass (which is IA),
- M is the total mass of the body,
- d is the distance between the two axes.
Step 4: Calculate Moments of Inertia
For axis A (through the center of mass):
IA=ICM
For axis B (not through the center of mass):
IB=IA+Md2
Step 5: Compare IA and IB
Since d is a positive distance (as B does not pass through the center of mass), we can conclude that:
IB=IA+Md2>IA
This implies that:
IA<IB
Conclusion
Thus, we have shown that the moment of inertia about the axis passing through the center of mass IA is less than the moment of inertia about the axis B that does not pass through the center of mass.
Final Answer
IA<IB
The moment of inertia of a body is a measure of how difficult it is to change its rotational motion about a given axis. It depends on the mass distribution of the body relative to the axis of rotation.
- Axis A passes through the center of mass (CM) of the body.
- Axis B does not pass through the center of mass.
The Parallel Axis Theorem states that if you know the moment of inertia ICM about an axis through the center of mass, you can find the moment of inertia about any parallel axis using the formula:
- IB is the moment of inertia about axis B,
- ICM is the moment of inertia about the center of mass (which is IA),
- M is the total mass of the body,
- d is the distance between the two axes.
For axis A (through the center of mass):
IA=ICM
IB=IA+Md2
Since d is a positive distance (as B does not pass through the center of mass), we can conclude that:
IB=IA+Md2>IA
IA<IB
Thus, we have shown that the moment of inertia about the axis passing through the center of mass IA is less than the moment of inertia about the axis B that does not pass through the center of mass.
IA<IB
Topper's Solved these Questions
- ROTATIONAL MECHANICSBook:HC VERMA ENGLISHChapter:ROTATIONAL MECHANICSExercise:Exercises
Explore 86 Videos
- ROTATIONAL MECHANICSBook:HC VERMA ENGLISHChapter:ROTATIONAL MECHANICSExercise:Questions for short Answer
Explore 21 Videos
- ROTATIONAL MECHANICSBook:HC VERMA ENGLISHChapter:ROTATIONAL MECHANICSExercise:Objective -1
Explore 26 Videos
- REST AND MOTION : KINEMATICSBook:HC VERMA ENGLISHChapter:REST AND MOTION : KINEMATICSExercise:Question for short Answer
Explore 13 Videos
- SIMPLE HARMONIC MOTIONBook:HC VERMA ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Question for short Answer
Explore 15 Videos
Similar Questions
Let IAandIB be moments of inertia of a body about two axes A and B respectively. The axis A passes through the centre of massof the body but B does not. Choose the correct option.
View SolutionThe moment of inertia of a body about a given axis of rotation depends upon :-
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View SolutionThe moment of inertia of a hollow cubical box of mass M and side a about an axis passing through the centres of two opposite faces is equal to.
View SolutionIf I1 is the moment of inertia of a thin rod about an axis perpendicular to its length and passing through its centre of mass and I2 is the moment of inertia of the ring about an axis perpendicular to plane of ring and passing through its centre formed by bending the rod, then
View Solutionfind moment of inertia about an axis yy which passes through the centre of mass of the two particle system as shown

View SolutionIf I1 is the moment of inertia of a thin rod about an axis perpendicular to its length and passing through its centre of mass and I2 is the moment of inertia (about central axis) of the ring formed by bending the rod, then the ratio of I1 to I2 is
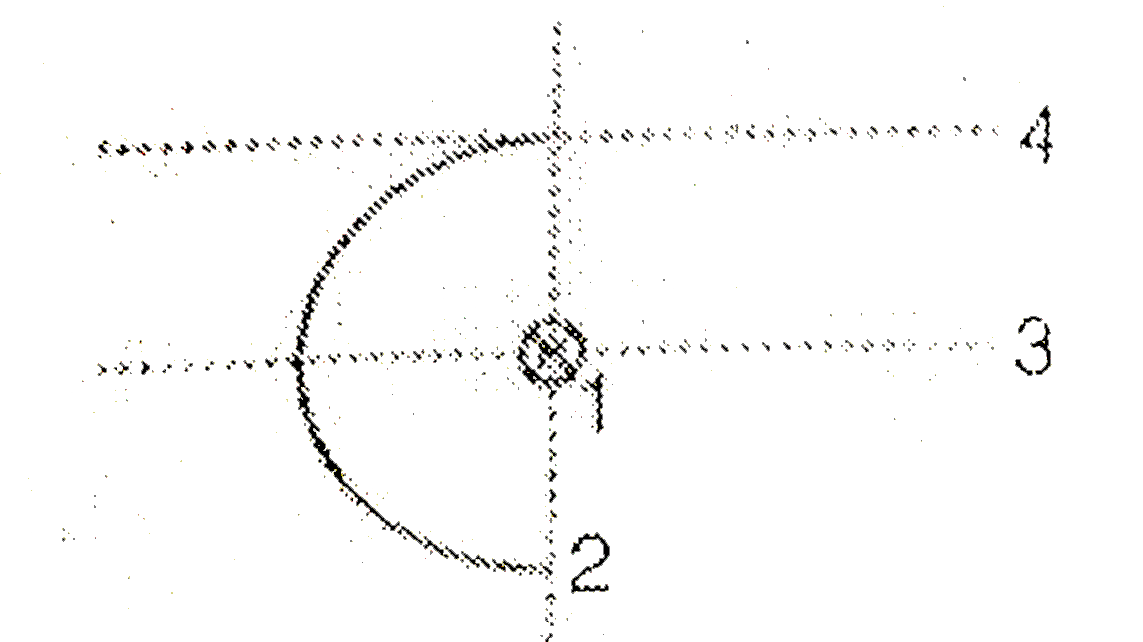
View SolutionA semi-circular ring has mass m and radius R as shown in figure. Let I1,I2,I3 and I4 be the moments of inertia about the four axes as shown . Axis 1 passes through centre and is perpendicular to plane of ring. Then , match the following.

View SolutionIn the given figure F=10N,R=1m, mass of the body is 2kg and moment of inertia of the body about an axis passing through O and perpendicular to the plane of the body is 4kgm2. O is the centre of mass of the body.

If the ground is smooth, what is the total kinetic energy of the body after 2s?
View SolutionThe moment of inertia of a cube of mass M and edge length a about an axis passing through one of its edge is
View Solution
