A sphere of catius r is kept on a concave of mirror radius of curation . The arrangement a kept on a horizontal tavke (the surface of concave mirror is fricationless and sliding not rolling). If the sphere is displaced from its equilibrium position and left, then it executes The period of oscillation will be
The correct Answer is:B
Tengental acceleration,
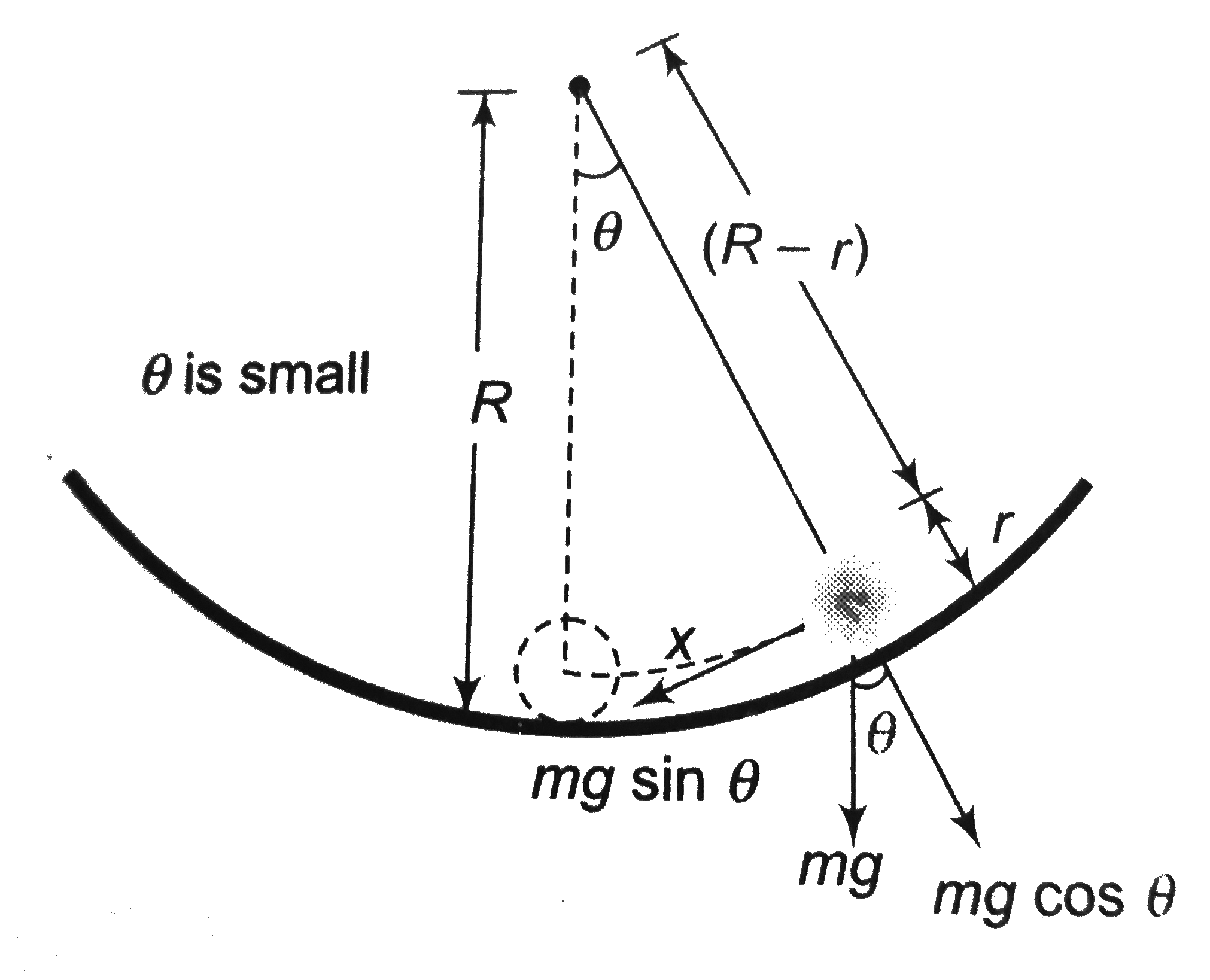
Motion is is with time period
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Superposition Of Shm And Compound Pendulum19videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Problems Based On Mixed Concepts24videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Spring Particle System24videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Chapter Test30videos
NEWTONS LAWS OF MOTION
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Chapter Test29videos
PROPERTIES OF MATTER
Similar Questions
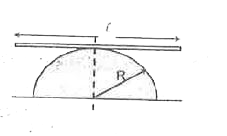
A uniform plank of length l and mass m is balanced on a fixed semi-circular plate of radius R as shown in the figure. If the plank is tilted slightly from its equilibrium position, and released, prove that it will execute S.H.M find the period of its oscillation.
 View Solution
View SolutionA small sphere is placed on a concave mirror of radius of curvature 'R' a little away from the centre.When the sphere is released it oscillates.Assuming the oscillation to be simple harmonic its time period is
View Solution
Knowledge Check
- Question 1 - Select One

A thin-walled tube of mass m and radius R has a rod of mass m and vry small cross section soldered on its inner surface. The side-view of the arrangement is as shown in the following figure. The entire arrangement is placed on a rough horizontal surface. The system is given a small angular displacement from its equilibrium position, as a result, the system performs oscillations. The time period of resulting oscillations if the tube rolls without slipping isA2π√4RgB2π√2RgC2π√RgDnone of these - Question 2 - Select One
The velocities of a body executing S.H.M. are 3 cm/s and 4 cm/s when the displacements from the mean position are 4 cm and 3 cm, then the period of oscillation is
A12πsBx2sC2xsD2πs - Question 3 - Select One
A sphere of radius 1 m is kept on a plank kept on horizontal surface. Accelerations of plank and centre of sphere are indicated in the figure.

If sphere is not slipping on the plank then its angular acceleration isA8rad/s2B6rad/s2C4rad/s2D2rad/s2
A concave mirror of radius R is kept on a horizontal table. Water (refractive index =mu.) is poured into it up to a height h. Where should an object be placed so that its image is formed on itself ?
 View Solution
View SolutionA sphere of mass M and radius R is held on the inner wall of a hollow sphere of mass 4M and radius 6R .The bigger sphere is kept on a smooth horizontal table and the centres of the two spheres lie on horizontal line.The system of two spheres is released from this position. The smaller sphere slides on the inner smooth wall to reach the other extreme position (shown in dotted line).The displacement of the centre of the larger sphere as the smaller sphere moves from one extreme to another is xcm. Value of x is: ( Take R=4.5cm) qquad y qquad yR Delta M
View SolutionA sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.
 View Solution
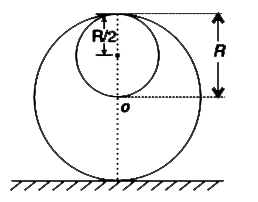
View SolutionA spherical cavity of radiusR2 is removed from a solid sphere of radius R as shown in fig. The sphere is placed on a rough horizontal surface as shown. The sphere is given a gentle push. Friction is large enough to prevent slippage. Prove that the sphere perform SHM and find the time period.
 View Solution
View SolutionA uniform thin ring of radius R and mass m suspended in a vertical plane from a point in its circumference. Its time period of oscillation is
View Solution

