A small sphere is placed on a concave mirror of radius of curvature 'R' a little away from the centre.When the sphere is released it oscillates.Assuming the oscillation to be simple harmonic its time period is
Step by step video & image solution for A small sphere is placed on a concave mirror of radius of curvature 'R' a little away from the centre.When the sphere is released it oscillates.Assuming the oscillation to be simple harmonic its time period is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
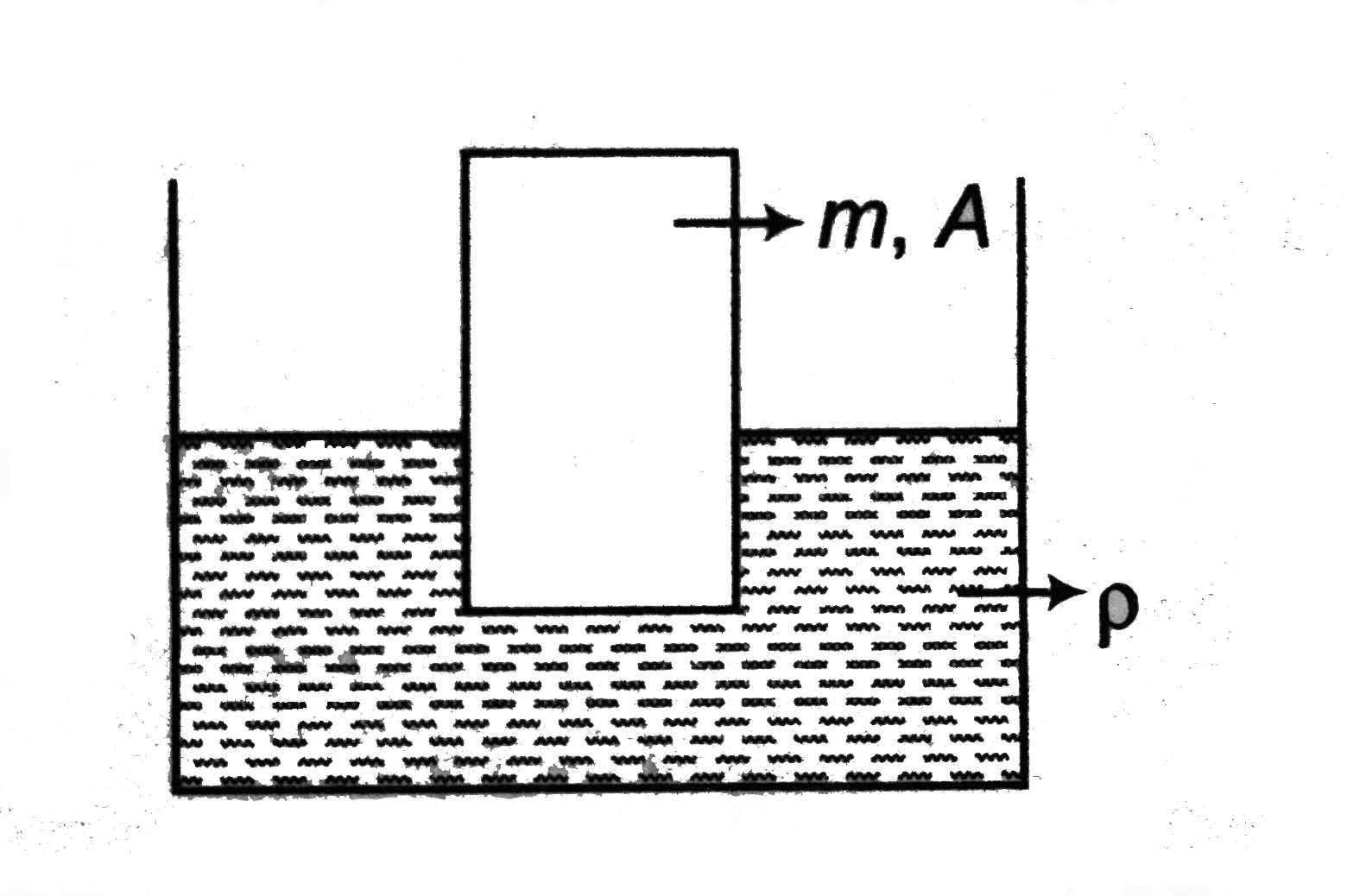
A plank of mass 'm' and area of cross - section A is floating in a non - viscous liquid of desity ρ. When displaced slightly from the mean position, it starts oscillating. Prove that oscillations are simple harmonic and find its time period.
View SolutionPositive charge Q is distributed uniformly over a circular ring of radius R. A particle having a mass m and a negative charge q, is placed on its axis at a distance x from the centre. Find the force on the particle. Assuming x ltltR, find the time period of oscillation of the particle if it is released from there.
View Solution
Knowledge Check
A small spherical steel ball is placed a little away from the centre of a large concave mirror of radius of curvature 2.5 m, if the ball is released, then the period of the motion will be (g=10m/s2)
Aπ/4sBπ/2sCπ/sD2πsForm the centre of a large concave mirror of radius of curvature 3 sm , a small sperical steel ball is placed at a little distance on the mirror itself . The ball is then released to execute oscillatory motion on the mirror . The time period of motion of the ball is
(Neglect friction and take g=10ms2A2.38sB3.06sC3.44sD4.22sA sphere of catius r is kept on a concave of mirror radius of curation R. The arrangement a kept on a horizontal tavke (the surface of concave mirror is fricationless and sliding not rolling). If the sphere is displaced from its equilibrium position and left, then it executes S.h.M. The period of oscillation will be
A2π ⎷((R−r)1.44)B2π√(R−rg)C2π√(rRa)D2π√(Rgr)
Show that for a small oscillations the motion of a simple pendulum is simple harmonic. Derive an expression of its time period.
View SolutionA ball of mass m kept at the centre of a string of length L is pulled from centre in perpendicular direction and released. Prove that motion of ball is simple harmonic and determine time period of oscillation
View SolutionA solid sphere of radius R is floating in a liquid of density σ with half of its volume submerged. If the sphere is slightly pushed and released , it starts axecuting simple harmonic motion. Find the frequency of these oscillations.
View SolutionThe bottom of a dip on a road has a radius of curvature R. A richshaw of mass M left a little away from the bottom oscillates about the dip. Deduce an expression for the period of oscillation.
View SolutionA point object at a distance 5R/3 from the pole of a concave mirror. R is the radius of curvature of mirror. Point object oscillates with amplitude of 1mm perpendicular to the principal axis.

Position of image when object is at O is :
View Solution
