Question

A sphere of mass m rolls without slipping on an inclined plane of inclination $\theta$. Find the linear acceleration of the sphere and the force of friction acting on it. What should be the minimum coefficient of static friction to support pure rolling?

Explanation

Suppose the radils f the sphere is r. The forces acting on the sphere are shown in ure. They are a weight mg, b. normal force N and c. friction f.

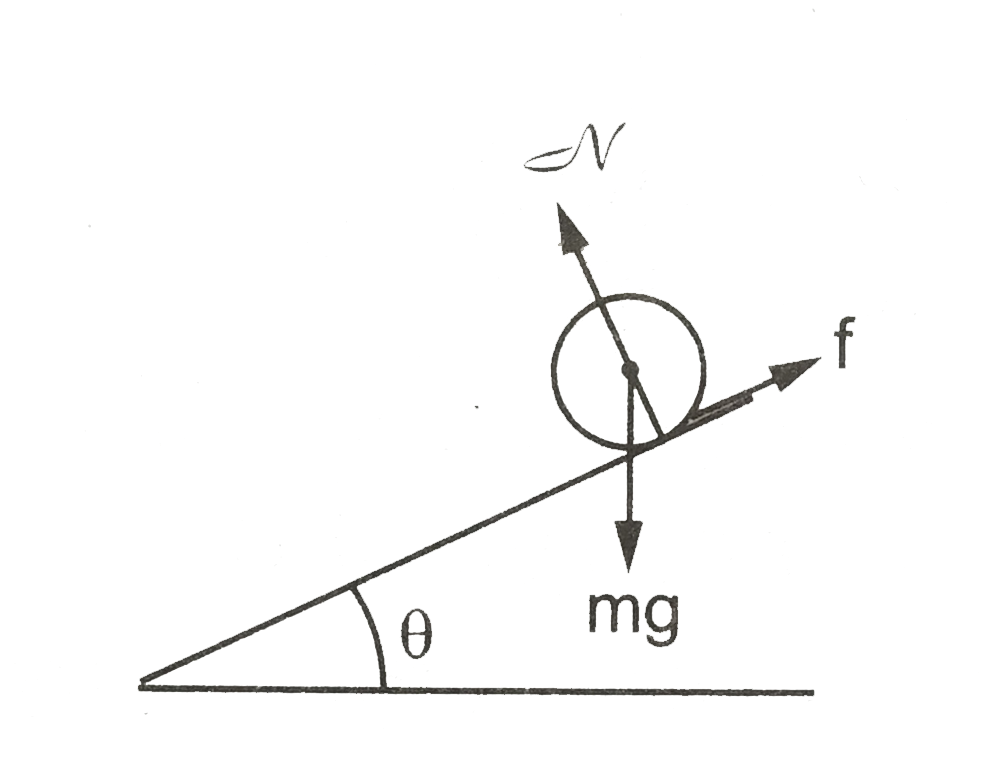
Let the linear acceleration of the sphere down the plane be a. The equation for the linear motion of the centre of mass is
`mg sintheta-f=ma`.............i
As the sphere rolls without slipping, its angular acceleration about the centre is `a/r. The equation of rotatioN/Al motion about the centre of mass is
`fr=(2/5mr^2)(a/r)`
or,` f=2/5ma`............ii
from i and ii
`a=5/7g sin theta`
and f=2/7 mg sintheta`
The normal force is equal to `mgcostheta` as there is no acceleration perpendicular to the incline. The maximum friction that can act is therefore, `mucostheta, where mu` is the coefficient of static friction. Thus, for pure rolling
`mucosthetagt2/7mg sintheta`
or `mugt2/7tantheta`