A spherical ball A of mass 4 kg, moving along a straight line strikes another spherical ball B of mass 1 kg at rest. After the collision, A and B move with velocities v1ms−1andv2ms−1 respectively making angles of 30∘and60∘ with respect to the original direction of motion of A. The ratio v1v2 will be
√34
4√3
1√3
√3
The correct Answer is:A
To solve the problem, we will use the principle of conservation of momentum. The momentum before the collision must equal the momentum after the collision for both the x and y components.
1. Identify the Given Data:
- Mass of ball A (m1) = 4 kg
- Mass of ball B (m2) = 1 kg
- Angle of ball A after collision = 30 degrees
- Angle of ball B after collision = 60 degrees
- Initial velocity of ball B = 0 m/s (at rest)
2. Set Up the Momentum Conservation Equations:
- Before the collision, the total momentum in the x-direction is only due to ball A:
Initial momentum=m1⋅vAi+m2⋅0=m1⋅vAi
- After the collision, the momentum in the x-direction is:
Final momentum in x=m1⋅v1⋅cos(30∘)+m2⋅v2⋅cos(60∘)
- The momentum in the y-direction before the collision is 0. After the collision, it is:
Final momentum in y=m1⋅v1⋅sin(30∘)−m2⋅v2⋅sin(60∘)
3. Apply Conservation of Momentum:
- For the x-direction:
m1⋅vAi=m1⋅v1⋅cos(30∘)+m2⋅v2⋅cos(60∘)
- For the y-direction:
0=m1⋅v1⋅sin(30∘)−m2⋅v2⋅sin(60∘)
4. Rearranging the y-direction Equation:
- Rearranging gives:
m1⋅v1⋅sin(30∘)=m2⋅v2⋅sin(60∘)
5. Substituting Known Values:
- Substitute m1=4kg, m2=1kg, sin(30∘)=12, and sin(60∘)=√32:
4⋅v1⋅12=1⋅v2⋅√32
- Simplifying this gives:
2v1=√32v2
6. Finding the Ratio v1v2:
- Rearranging gives:
v1v2=√34
Final Answer:
The ratio v1v2=√34.
- Mass of ball A (m1) = 4 kg
- Mass of ball B (m2) = 1 kg
- Angle of ball A after collision = 30 degrees
- Angle of ball B after collision = 60 degrees
- Initial velocity of ball B = 0 m/s (at rest)
- Before the collision, the total momentum in the x-direction is only due to ball A:
Initial momentum=m1⋅vAi+m2⋅0=m1⋅vAi
- After the collision, the momentum in the x-direction is:
Final momentum in x=m1⋅v1⋅cos(30∘)+m2⋅v2⋅cos(60∘)
- The momentum in the y-direction before the collision is 0. After the collision, it is:
Final momentum in y=m1⋅v1⋅sin(30∘)−m2⋅v2⋅sin(60∘)
- For the x-direction:
m1⋅vAi=m1⋅v1⋅cos(30∘)+m2⋅v2⋅cos(60∘)
- For the y-direction:
0=m1⋅v1⋅sin(30∘)−m2⋅v2⋅sin(60∘)
- Rearranging gives:
m1⋅v1⋅sin(30∘)=m2⋅v2⋅sin(60∘)
- Substitute m1=4kg, m2=1kg, sin(30∘)=12, and sin(60∘)=√32:
4⋅v1⋅12=1⋅v2⋅√32
- Simplifying this gives:
2v1=√32v2
- Rearranging gives:
v1v2=√34
The ratio v1v2=√34.
Topper's Solved these Questions
- WORK , ENERGY AND POWERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WORK , ENERGY AND POWEREXERCISE - NCERT
18 Videos
- WORK , ENERGY AND POWERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WORK , ENERGY AND POWEREXERCISE - ASSERTION & REASON
15 Videos
- WAVESBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVESEXERCISE - Assertion And Reason
15 Videos
Similar Questions
A smooth sphere of mass M moving with velocity u directly collides elastically with another sphere of mass m at rest. After collision their final velocities are V and v respectively. The value of v is
View SolutionA smooth sphere of mass M moving with velocity u directly collides elastically with another sphere of mass m at rest. After collision their final velocities are V and v respectively. The value of v is
View Solution
Knowledge Check
A spherical ball of mass m1 collides head on with another ball of mass m2 at rest . The collision is elastic . The fraction of kinetic energy lost by m1 is :
A4m1m2(m1+m2)2Bm1m1+m2Cm2m1+m2Dm1m2(m1+m2)2
A ball of mass 1 kg moving with a velocity of 0.4 ms−1 collides with another stationary ball. After the collision, the first ball moves with a velocity of 0.3ms1 in a direction making an angle of 90∘ with its initial direction. The momentum of the second ball after the collision will be (in kg ms−1)
View SolutionA ball of mass m moving with velocity v collides head on elastically with another identical ball moving with velocity - V. After collision
View SolutionA spherical ball of mass 1kg moving with a uniform speed of 1m/s collides symmetrically with two identical spherical balls of mass 1kg each at rest touching each other. If the two balls move with 0.5m/s in two directions at the same angle of 60∘ with the direction of the first ball, the loss of kinetic energy on account of the collision is :-
View SolutionTwo particles 1and2 move with velocities →v1 and →v2 making the angles θ1andθ2 with the line joining them, respectively. Find angular velocity of relative→1.
 .
.
View SolutionA ball of mass 1kg moving with 4m−1 along +x-axis collides elastically with an another ball of mass 2kg moving with 6m/s is opposite direction. Find their velocities after collision.
View SolutionIn fig., blocks A and B move with velocities v1 and v2 along horizontal direction. Find the ratio of v1/v2
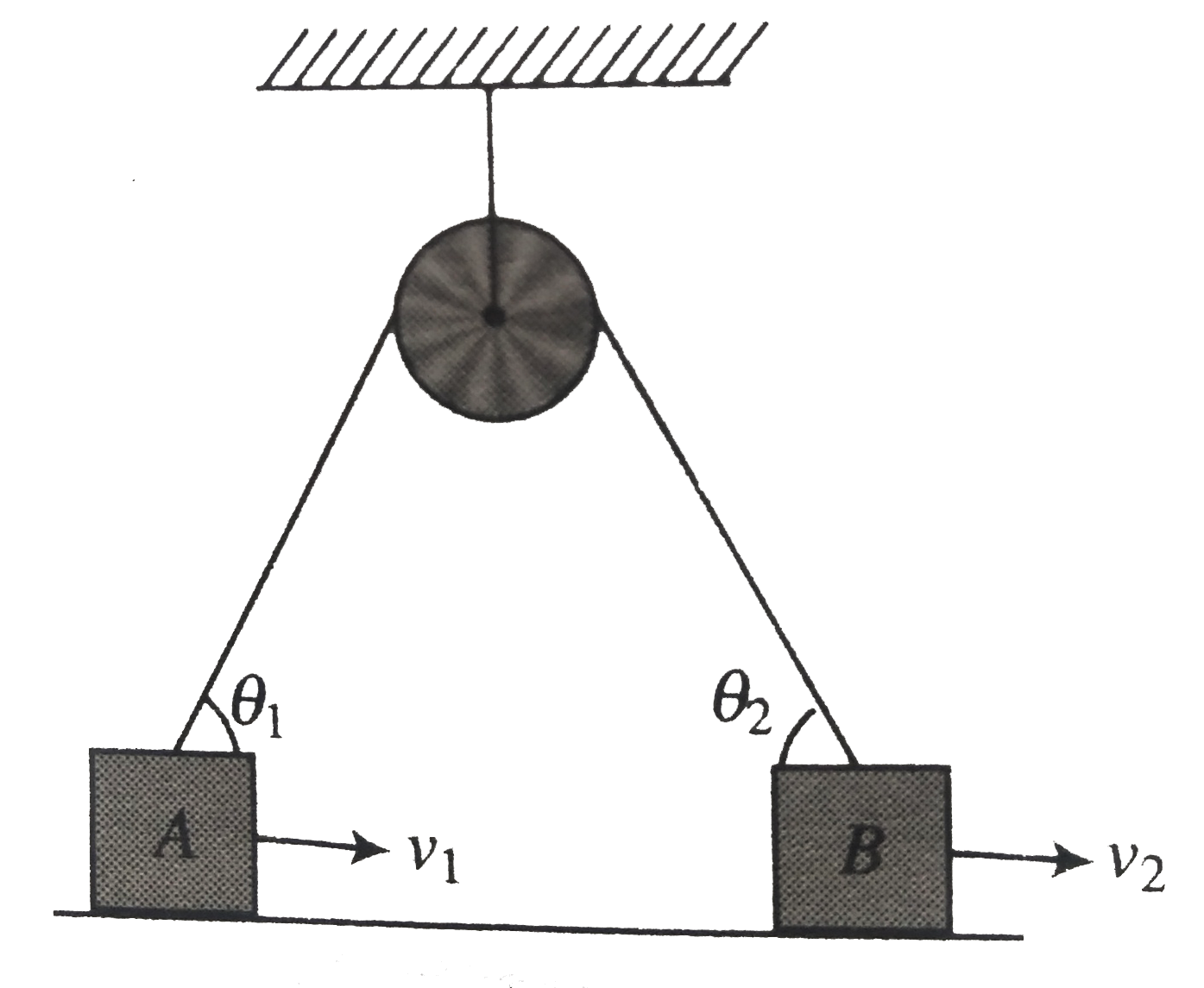
View SolutionA billiard ball moving at a speed of 6.6 ms–1 strikes an identical stationary ball a glancingblow. After the collision, one ball is found to be moving at a speed of 3.3, ms–1 in a direction making an angle of 60º with the original line of motion. The velocity of the other ball is
View Solution
