A billiard ball moving at a speed of 6.6 ms–1 strikes an identical stationary ball a glancingblow. After the collision, one ball is found to be moving at a speed of 3.3, ms–1 in a direction making an angle of 60º with the original line of motion. The velocity of the other ball is
(3)1/2m/s at 30∘ to the original direction.
1m/s at 60∘ to the original direction.
(3)1/2m/s at 60∘ to the original direction.
1 m/s at 30∘ to the original direction.
The correct Answer is:A
To solve the problem, we will apply the principle of conservation of momentum. Let's break down the steps:
Step 1: Understand the initial and final conditions.
- Initially, we have one billiard ball moving with a speed of v=6.6m/s and an identical stationary ball (speed = 0).
- After the collision, one ball moves with a speed of v′=3.3m/s at an angle of 60∘ to the original line of motion.
Step 2: Set up the momentum conservation equation.
- Since the masses of the balls are identical, we can ignore the mass in our calculations. The momentum before and after the collision must be equal:
Initial Momentum=Final Momentum
This can be expressed as:
m⋅v=m⋅v′+m⋅v0
where v0 is the velocity of the second ball after the collision.
Step 3: Break down the vectors.
- We can break the velocities into components. Let’s denote the initial velocity vector as →v and the final velocity of the first ball as →v′.
- The initial momentum vector is:
→pinitial=m⋅→v
The final momentum vector is:
→pfinal=m⋅→v′+m⋅→v0
Step 4: Use vector subtraction to find v0.
- Rearranging the momentum conservation equation gives:
→v0=→v−→v′
Step 5: Calculate the magnitude of v0.
- We will use the formula for the magnitude of the difference of two vectors:
|→v0|=√|→v|2+|→v′|2−2|→v||→v′|cos(θ)
where θ=60∘.
Step 6: Substitute the values.
- Substitute |→v|=6.6m/s, |→v′|=3.3m/s, and cos(60∘)=0.5:
|→v0|=√(6.6)2+(3.3)2−2⋅(6.6)⋅(3.3)⋅0.5
Step 7: Calculate each term.
- Calculate (6.6)2=43.56
- Calculate (3.3)2=10.89
- Calculate 2⋅(6.6)⋅(3.3)⋅0.5=21.78
Step 8: Combine the results.
- Now plug these values back into the equation:
|→v0|=√43.56+10.89−21.78
|→v0|=√32.67
|→v0|≈5.7m/s
Final Answer:
The velocity of the other ball after the collision is approximately 5.7m/s.
---
- Initially, we have one billiard ball moving with a speed of v=6.6m/s and an identical stationary ball (speed = 0).
- After the collision, one ball moves with a speed of v′=3.3m/s at an angle of 60∘ to the original line of motion.
- Since the masses of the balls are identical, we can ignore the mass in our calculations. The momentum before and after the collision must be equal:
Initial Momentum=Final Momentum
This can be expressed as:
m⋅v=m⋅v′+m⋅v0
where v0 is the velocity of the second ball after the collision.
- We can break the velocities into components. Let’s denote the initial velocity vector as →v and the final velocity of the first ball as →v′.
- The initial momentum vector is:
→pinitial=m⋅→v
The final momentum vector is:
→pfinal=m⋅→v′+m⋅→v0
- Rearranging the momentum conservation equation gives:
→v0=→v−→v′
- We will use the formula for the magnitude of the difference of two vectors:
|→v0|=√|→v|2+|→v′|2−2|→v||→v′|cos(θ)
where θ=60∘.
- Substitute |→v|=6.6m/s, |→v′|=3.3m/s, and cos(60∘)=0.5:
|→v0|=√(6.6)2+(3.3)2−2⋅(6.6)⋅(3.3)⋅0.5
- Calculate (6.6)2=43.56
- Calculate (3.3)2=10.89
- Calculate 2⋅(6.6)⋅(3.3)⋅0.5=21.78
- Now plug these values back into the equation:
|→v0|=√43.56+10.89−21.78
|→v0|=√32.67
|→v0|≈5.7m/s
The velocity of the other ball after the collision is approximately 5.7m/s.
Topper's Solved these Questions
- WORK ENERGY AND POWER BOOK - VMC MODULES ENGLISHCHAPTER - WORK ENERGY AND POWER EXERCISE - EFFICIENT
50 Videos
- WORK ENERGY AND POWER BOOK - VMC MODULES ENGLISHCHAPTER - WORK ENERGY AND POWER EXERCISE - IMPECCABLE
54 Videos
- WORK ENERGY AND POWER BOOK - VMC MODULES ENGLISHCHAPTER - WORK ENERGY AND POWER EXERCISE - IMPECCABLE
54 Videos
- WAVE MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - WAVE MOTIONEXERCISE - JEE ADVANCED ARCHIVE LEVEL 2 (TRUE FALSE TYPE)
4 Videos
Similar Questions
A ball of mass 1 kg moving with a velocity of 0.4 ms−1 collides with another stationary ball. After the collision, the first ball moves with a velocity of 0.3ms1 in a direction making an angle of 90∘ with its initial direction. The momentum of the second ball after the collision will be (in kg ms−1)
View SolutionA ball moving with a speed of 9ms−1 strikes an identical stationary ball such that after the collision the direction of each ball makes an angle of 30∘ with the original line of motion. The speeds of two balls after the collision is
View Solution
Knowledge Check
A ball , moving with a speed of 10√3m/s , strikes an identical stationary ball such that after the collision , the direction of each ball makes an angle of 30∘with the original line of motion. The speeds of two balla after the collision are , respectively.
A3ms−1,3ms−1B3√3ms−1,3√3ms−1C3√3ms−1,3ms−1D3ms−1,3√3ms−1A ball weighing 4 kg and moving with velocity of 8 m/sec. Collides with a stationary ball of mass 12 kg. After the collision, the two balls move together. The final velocity is
A0B2 m/secC8 m/secD16 m/secA spherical ball A of mass 4 kg, moving along a straight line strikes another spherical ball B of mass 1 kg at rest. After the collision, A and B move with velocities v1ms−1andv2ms−1 respectively making angles of 30∘and60∘ with respect to the original direction of motion of A. The ratio v1v2 will be
A√34B4√3C1√3D√3
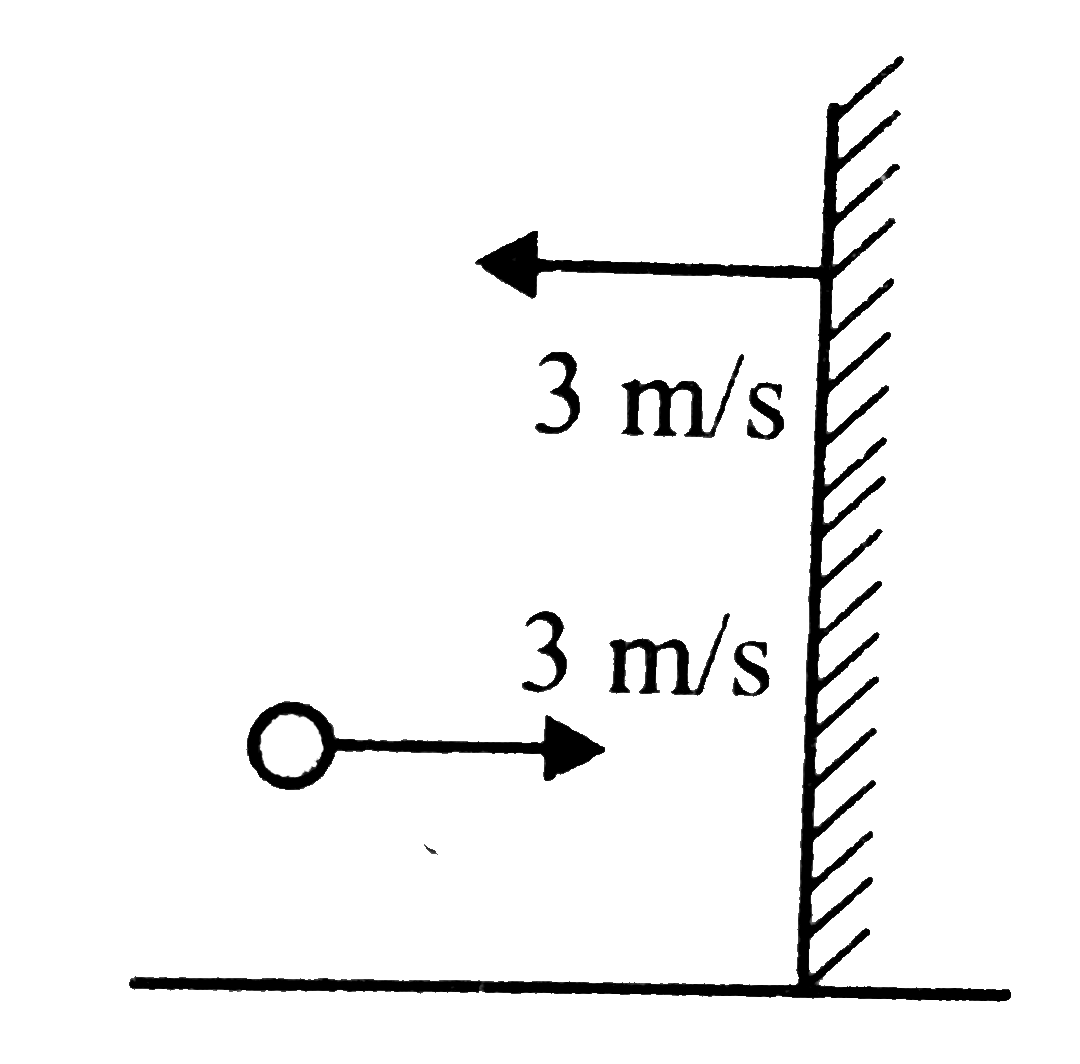
A highly elastic ball moving at a speed of 3m/s approaches a wall moving towards it with a speed of 3m/s. After the collision. the speed of the ball will be
View SolutionA bullet of mass m moving at a speed v hits a ball of mass M kept at rest. A small part having mass m ′ breaks from the ball and sticks to the bullet. The remaining ball is found to move at a speed v 1 , in the direction of the bullet. Find the velocity of the bullet after the collision.
View SolutionTwo identical billiard balls undergo an oblique elastic collision. Initially, one of the balls is stationary. If the initially stationary ball after collision moves in a direction which makes an angle of 37∘ with direction of initial motion of the moving ball, then the angle through which initially moving ball will be deflected is
View SolutionCalculate the de Broglie wavelength of a ball of mass 0.1kg moving with a speed of 30ms−1
View SolutionA spherical ball of mass 1kg moving with a uniform speed of 1m/s collides symmetrically with two identical spherical balls of mass 1kg each at rest touching each other. If the two balls move with 0.5m/s in two directions at the same angle of 60∘ with the direction of the first ball, the loss of kinetic energy on account of the collision is :-
View Solution