A spherical shell of radius with a uniform charge q has a point charge at its center. Find the work performed by the electric forces during the shell expansion from radius to radius .
To find the work performed by the electric forces during the expansion of a spherical shell from radius R1 to radius R2, we will follow these steps:
Step 1: Understand the System
We have a spherical shell of radius R1 with a uniform charge q and a point charge q0 located at its center. We need to calculate the work done when the radius of the shell changes from R1 to R2.
Step 2: Calculate Initial Potential Energy Uinitial
The total initial potential energy Uinitial consists of two parts:
1. Self-energy of the spherical shell.
2. Interaction energy between the shell and the point charge.
The self-energy of a uniformly charged spherical shell of radius R1 is given by:
Uself=q28πϵ0R1
The interaction energy between the charge q on the shell and the charge q0 at the center is given by:
Uinteraction=14πϵ0qq0R1
Thus, the total initial potential energy is:
Uinitial=Uself+Uinteraction=q28πϵ0R1+14πϵ0qq0R1
Step 3: Calculate Final Potential Energy Ufinal
Similarly, we calculate the final potential energy Ufinal when the radius is R2.
The self-energy of the spherical shell at radius R2 is:
Uself=q28πϵ0R2
The interaction energy at radius R2 is:
Uinteraction=14πϵ0qq0R2
Thus, the total final potential energy is:
Ufinal=q28πϵ0R2+14πϵ0qq0R2
Step 4: Calculate Work Done
The work done W by the electric forces during the expansion of the shell is given by the difference in potential energy:
W=Ufinal−Uinitial
Substituting the expressions for Uinitial and Ufinal:
W=(q28πϵ0R2+14πϵ0qq0R2)−(q28πϵ0R1+14πϵ0qq0R1)
Step 5: Simplify the Expression
Now, we can simplify this expression:
W=q28πϵ0(1R2−1R1)+qq04πϵ0(1R2−1R1)
Factoring out the common term:
W=(1R2−1R1)(q28πϵ0+qq04πϵ0)
Final Result
Thus, the work performed by the electric forces during the expansion of the shell is:
W=(1R2−1R1)q4πϵ0(q2+q0)
We have a spherical shell of radius R1 with a uniform charge q and a point charge q0 located at its center. We need to calculate the work done when the radius of the shell changes from R1 to R2.
The total initial potential energy Uinitial consists of two parts:
1. Self-energy of the spherical shell.
2. Interaction energy between the shell and the point charge.
Uself=q28πϵ0R1
Uinteraction=14πϵ0qq0R1
Uinitial=Uself+Uinteraction=q28πϵ0R1+14πϵ0qq0R1
Similarly, we calculate the final potential energy Ufinal when the radius is R2.
Uself=q28πϵ0R2
Uinteraction=14πϵ0qq0R2
Ufinal=q28πϵ0R2+14πϵ0qq0R2
The work done W by the electric forces during the expansion of the shell is given by the difference in potential energy:
W=Ufinal−Uinitial
W=(q28πϵ0R2+14πϵ0qq0R2)−(q28πϵ0R1+14πϵ0qq0R1)
Now, we can simplify this expression:
W=q28πϵ0(1R2−1R1)+qq04πϵ0(1R2−1R1)
W=(1R2−1R1)(q28πϵ0+qq04πϵ0)
Thus, the work performed by the electric forces during the expansion of the shell is:
W=(1R2−1R1)q4πϵ0(q2+q0)
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Examples
9 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - Exercise 3.1
23 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
A spherical shell of radius R1 with uniform charge q is expanded to a radius R2. Find the work performed by the electric forces in this process.
View SolutionA sperical shell of radius R with uniform charge q is expanded to a radius 2R. Find the work perfomed by the electric forces and external agent against electric forces in this process.
View SolutionA spherical shell of radius R has a uniformly distributed charge ,then electric field varies as
View SolutionA spherical shell of radius R carries a uniformly distributed charge q. The electrical forces arising cause the ex-pansion of the shell. Find the mechanical stress in the shell.
View SolutionA conducting shell of radius R carries charge −Q. A point charge +Q is placed at the centre. The electric field E varies with distance r (from the centre of the shell) as
View SolutionA spherical shell having charge +Q (uniformly distributed) and a point charge +q0 are placed as shown. Find the force between shell and the point charge (r>>R).
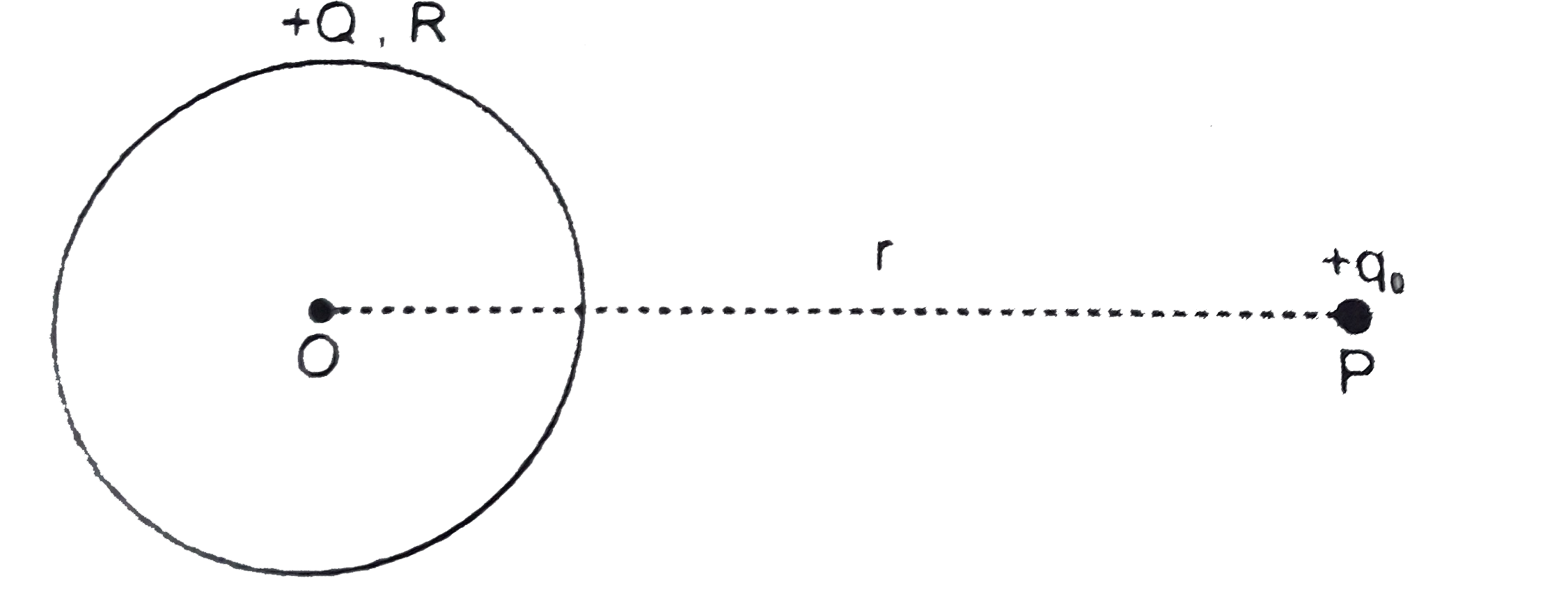
View SolutionA non-conducting spherical shell of radius R surrounds a point charge q (q at center). The electric flux through a cap of the shell of half angle θ is:
View SolutionA non-conducting spherical shell of radius R surrounds a point charge q (q at center). The electric flux through a cap of the shell of half angle θ is:
View SolutionA spherical shell of radius R is given charge 3q on its surface and a point charge q is placed at distance R/2 from its centre C. Also there is a charge 2q placed outside the shell at a distance of 2R as shown. Then

View SolutionA conducting shell of radius R carries charge–Q. A point charge +Q is placed at the centre of shell. The electric field E varies with distance r (from the centre of the shell) as :
View Solution
