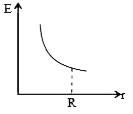
A conducting shell of radius R carries charge–Q. A point charge +Q is placed at the centre of shell. The electric field E varies with distance r (from the centre of the shell) as :


The correct Answer is:A
To solve the problem of how the electric field E varies with distance r from the center of a conducting shell carrying charge −Q with a point charge +Q placed at its center, we can follow these steps:
Step 1: Understand the Setup
We have a conducting shell of radius R with a charge of −Q and a point charge +Q at the center. The electric field inside and outside the shell will be influenced by these charges.
Step 2: Analyze the Electric Field Inside the Shell (0 < r < R)
- For a Gaussian surface inside the shell (where r<R), we consider the charge +Q at the center.
- According to Gauss's law, the electric flux through the Gaussian surface is given by:
Φ=Qinsideϵ0
where Qinside=+Q.
- The electric field E at a distance r from the center is uniform over the surface of the Gaussian sphere, so:
Φ=E⋅4πr2
- Setting the two expressions for flux equal gives:
E⋅4πr2=Qϵ0
Therefore, the electric field E at distance r is:
E=Q4πϵ0r2
- This shows that the electric field inside the shell varies inversely with the square of the distance r.
Step 3: Analyze the Electric Field on the Surface of the Shell (r = R)
- At the surface of the shell (when r=R), the electric field is still given by the same formula:
E=Q4πϵ0R2
Step 4: Analyze the Electric Field Outside the Shell (r > R)
- For a Gaussian surface outside the shell (where r>R), we need to consider the total charge enclosed by the Gaussian surface.
- The total charge inside the Gaussian surface is:
Qtotal=+Q+(−Q)=0
- Therefore, according to Gauss's law:
Φ=Qinsideϵ0=0
- This implies that the electric field E outside the shell is:
E=0
Step 5: Summarize the Results
- For 0<r<R: E=Q4πϵ0r2 (inversely proportional to r2)
- For r=R: E=Q4πϵ0R2
- For r>R: E=0
Final Answer
The electric field E varies with distance r as follows:
- It decreases with r2 for 0<r<R,
- It is a constant value at r=R,
- It becomes zero for r>R.
We have a conducting shell of radius R with a charge of −Q and a point charge +Q at the center. The electric field inside and outside the shell will be influenced by these charges.
- For a Gaussian surface inside the shell (where r<R), we consider the charge +Q at the center.
- According to Gauss's law, the electric flux through the Gaussian surface is given by:
Φ=Qinsideϵ0
where Qinside=+Q.
Φ=E⋅4πr2
E⋅4πr2=Qϵ0
Therefore, the electric field E at distance r is:
E=Q4πϵ0r2
- This shows that the electric field inside the shell varies inversely with the square of the distance r.
- At the surface of the shell (when r=R), the electric field is still given by the same formula:
E=Q4πϵ0R2
- For a Gaussian surface outside the shell (where r>R), we need to consider the total charge enclosed by the Gaussian surface.
- The total charge inside the Gaussian surface is:
Qtotal=+Q+(−Q)=0
- Therefore, according to Gauss's law:
Φ=Qinsideϵ0=0
- This implies that the electric field E outside the shell is:
E=0
- For 0<r<R: E=Q4πϵ0r2 (inversely proportional to r2)
- For r=R: E=Q4πϵ0R2
- For r>R: E=0
The electric field E varies with distance r as follows:
- It decreases with r2 for 0<r<R,
- It is a constant value at r=R,
- It becomes zero for r>R.
Similar Questions
A conducting shell of radius R carries charge −Q. A point charge +Q is placed at the centre. The electric field E varies with distance r (from the centre of the shell) as
View SolutionA thin spherical conducting shell of radius R has a charge q. Another charge Q is placed at the centre of the shell. The electrostatic potential at a point P a distance R2 from the centre of the shell is
View SolutionA thin spherical conducting shell of radius R has a charge q. Another charge Q is placed at the centre of the shell. The electrostatic potential at a point P a distance R/2 from the centre of the shell is
View SolutionConsider a thin conducting shell of radius R carrying total charge Q. Two point charges Q and 2Q are placed on points A and B, which are at a distances of R2 and 2R from the center of the cell respectively as shown in the figure. If the cell is earthed how much charge will flow to the earth?
View SolutionA point charge Q is placed inside a conducting spherical shell of inner radius 3R and outer radius 5R at a distance R from the centre of the shell. The electric potential at the centre of the shell will be
View SolutionA spherical conducting shell of inner radius r1 and outer radius r2 has a charge Q.
(a) A charge q is placed at the center of the shell. What is the surface charge density on the inner and outer surfaces of the shell ?
(b) Is the electric field intensity inside a cavity (with no charge) zero, even if the shell is not spherical, but has any irregular shape ? Explain.
View SolutionA metallic spherical shell of radius R has a charge -Q on it. A point charge +Q is placed at the centre of the shell. Which of the graphs shown below may correctly represent the variation of electric field E with distance r from the centre of shell ?
View SolutionA point charge Q is placed at the centre of a spherical conducting shell. A total charge of -q is placed on the shell. The magnitude of the electric field at point P1 at a distance R1 from the centre is X. The magnitude of the electric field due to induced charges at point P2 a distance R2 from the centre is Y. The values of X and Y are respectively.

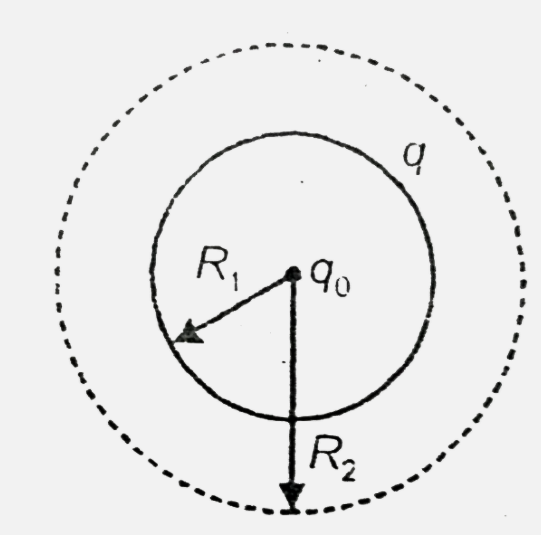
View SolutionA sperical shell is uniformly charged by a charge q. A point charge q0 is at its centre , then
View SolutionA point charge .q. is placed at the centre of an uncharged conducting shell of inner radius R and outer radius 2R. If the point charge is removed from the centre of the shell, to infinity (without any electric contact with the shell). Work done by electric force is
View Solution

