A spider is on the surface of a glass sphere with a refractive inndex of 1.5 . An insect crawls on the other side of the sphere as shown in Fig. For what maximum value of θ will the spider be able to still see the insect. Assume the spiders eye is in air.
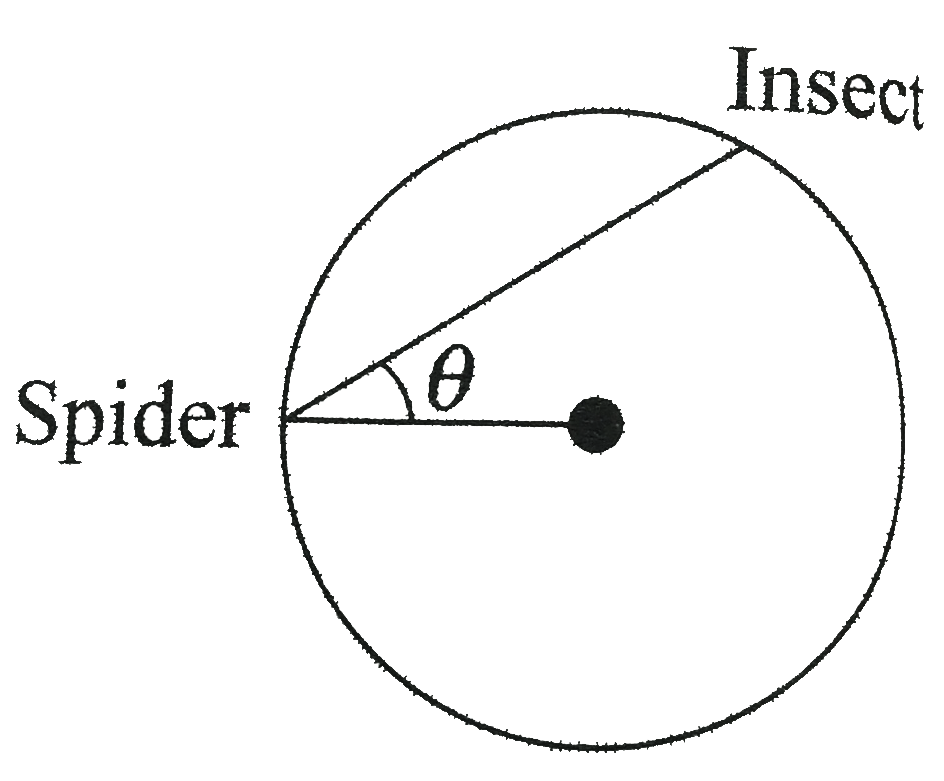
The spider will be able to see the insect if a ray of light from the insect reaches the spider's eye. If the angle of incidence of the beam is greater than the cirtical angle for the glass-air interface, the ray will be reflected within the glass sphere and will not emerge from it. Consequently, the spider will not be able to see the insect. Therefore, the angle θ must be greater than the critical angle for the glass- air interface. That is,
θ>sin−1[11⋅5]⇒θ>sin−1(23)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Solved Examples15videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.114videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.315videos
ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit27videos
HEATING EFFECT OF CURRENT
Similar Questions
A spider and a fly are on the surface of a glass sphere. As the fly moves on the surface, find the maximum area on the glass sphere for the spider to be able to see it? Assume that the radius of the sphere (R) is much larger than the sizes of the spider and the fly. take the refractive index of glass μg to be equal to √2.
View SolutionA glass sphere of refractive index 1.5 forms the real image of object O at point I as shown in the figure when kept in air of refractive index 1. If the value of x is kR. Find k
View SolutionA rectangular slab ABCD, of refractive index n1 , is immersed in water of refractive index n2(n1<n2). A ray of light is incident at the surface AB of the slab as shown in Fig. Find the maximum value of angle of incidence αmax, such that the ray comes out only from the other surface CD.
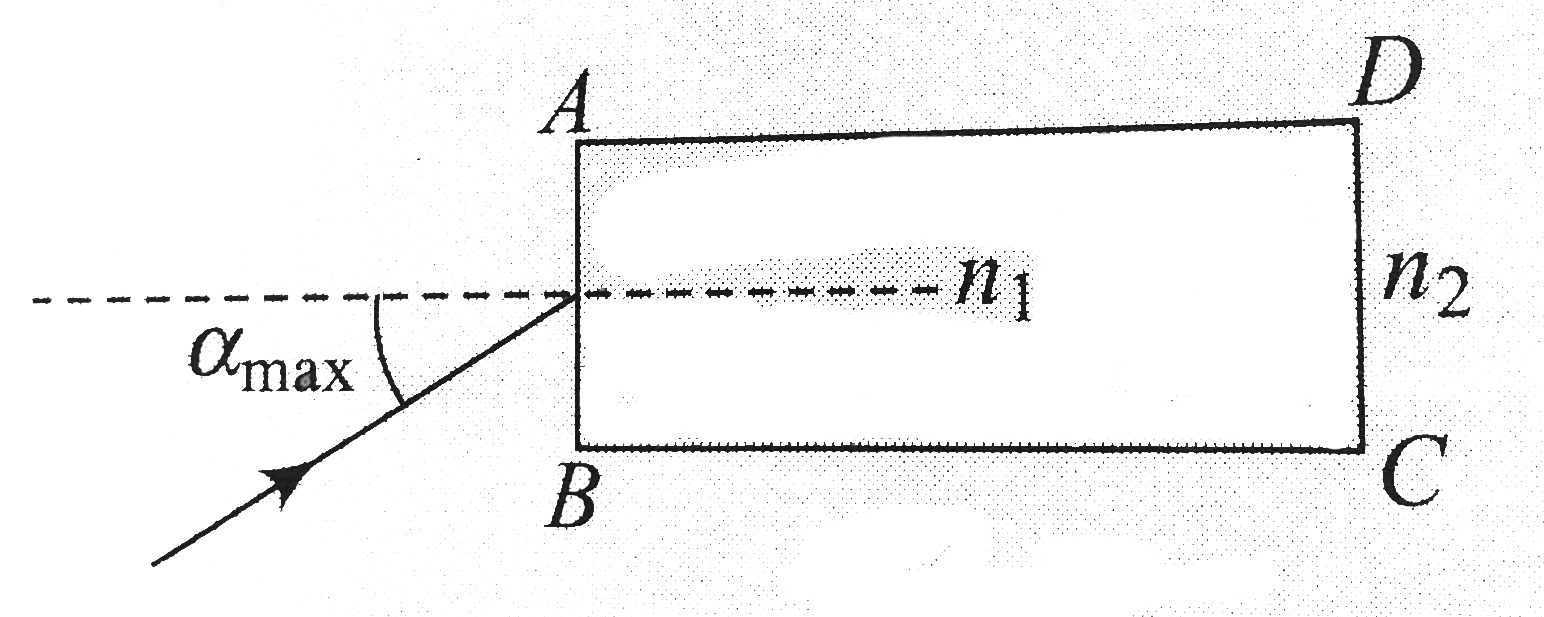 View Solution
View SolutionDoes the escape speed of a body from the earth depend on.
(i)mass of the body
(ii)the location from where it is projected
(iii)the direction of projection
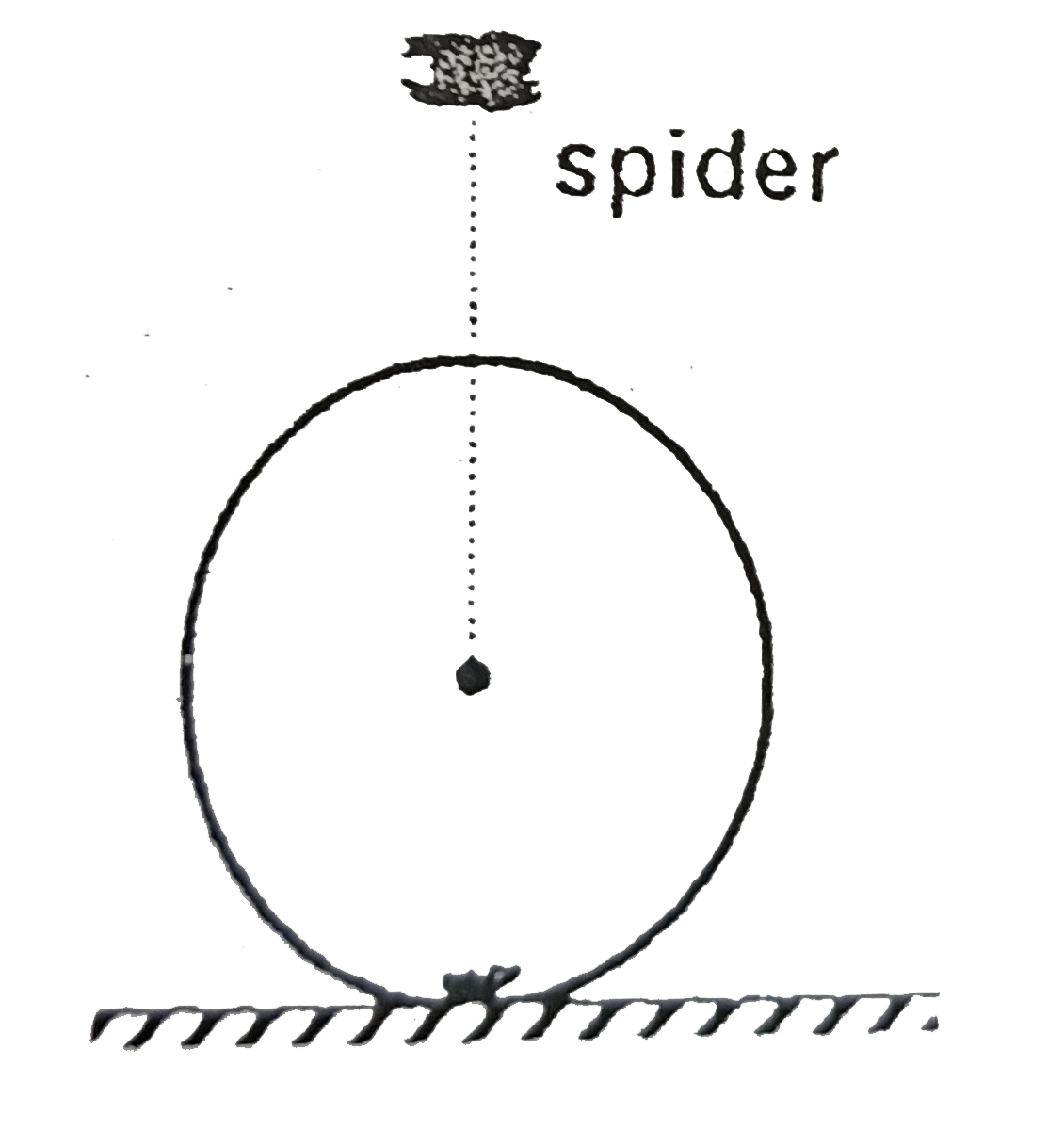
(iv)the height of the location from where the body is launched?View SolutionA spider is hanging by means of its own silk thread directly above a transparent fixed sphere of radius R=20cm as shown in the figure. The refractive index of the material of the sphere is equal to √2 and the height of the spider from the centre of the sphere is 2R(=40cm). An insect, initially sitting at the bottom, starts crawling on the sphere along a vertical circular path with the constant speed of π/4cm/s. For how long time the insect will be invisible for the spider, assume that it crawls once round the vertical circle.
 View Solution
View SolutionThere is an insect a cabin eying towards thick glass plate P1, Insect sees the images of light source acrss the glass plate P1 outside tha chain. Cabin is made of thick glass plates of refractive index μ=32 and thickness 3cm. Insect is eying from the middle of the cabin as shown in figure. (glass plates are partially reflective and consider only paraxial rays)

At what distance (from eye of insect) will the eye see the image ?View SolutionA hemispherical portion of the surface of a solid glass sphere (mu = 1.5) of radius r is silvered to make the inner side reflecting. An object is placed on the axis of the hemisphere at a distance 3r from the centre of the sphere. The light from the object is refracted at the unsilvered part, then reflected from the silvered part and again refracted at the unsilvered part. Locate the final image formed.
View SolutionA uniform bar of length 12L and mass 48m is supported horizontally on two smooth tables as shown in the figure. A small moth (an insect) of mass 8m is sitting on end A of the rod and a spider (an insect) of mass 16m is sitting on the other end B. Both the insects start moving towards each other along the rod with moth moving at speed 2v and the spider at half of this speed. They meet at a point P on the rod and the spider eats the moth. After this the spider moves with a velocity v/2 relative to the rod towards the end A. The spider takes negligible time in eating the insect. Also, let v=L/T, where T is a constant having value 4sec.The speed of the bar after the spider eats up the moth and moves towards A is
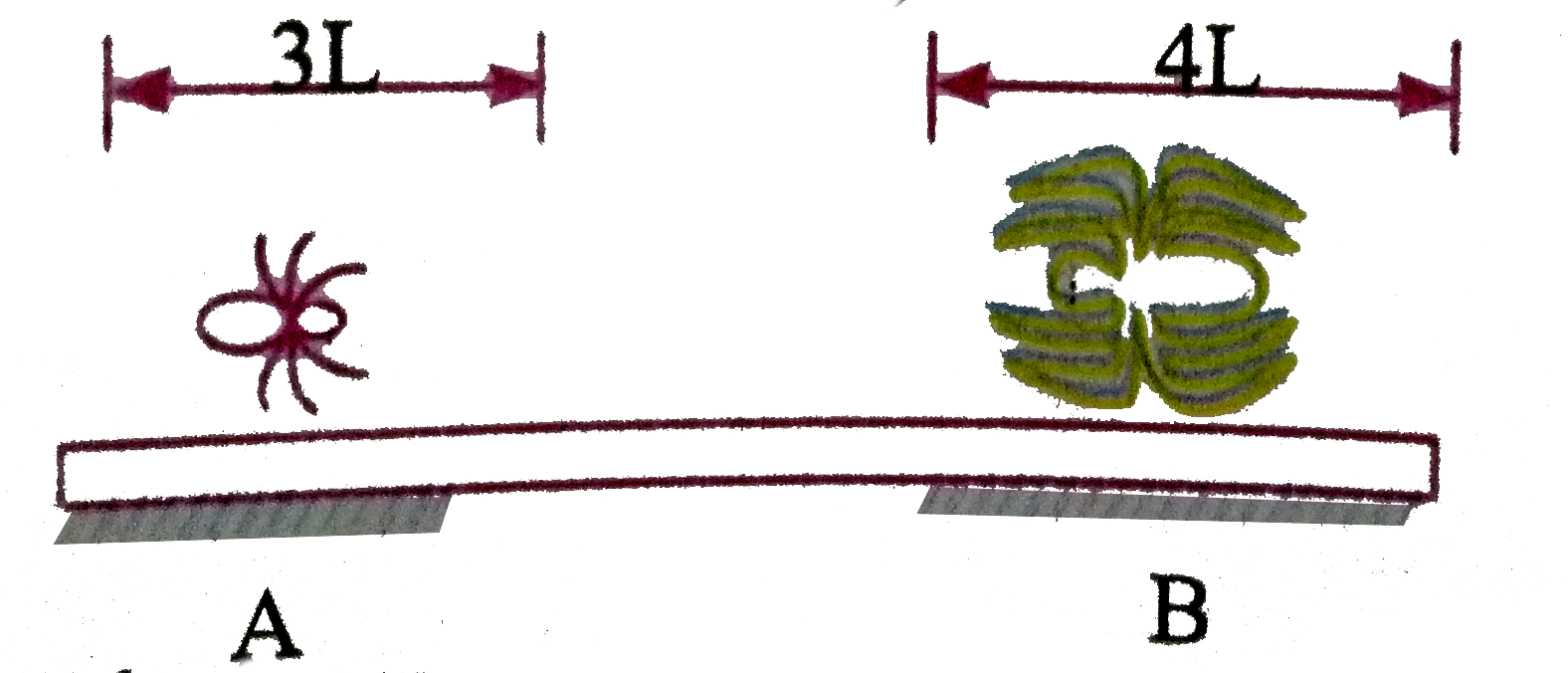 View Solution
View SolutionA uniform bar of length 12L and mass 48m is supported horizontally on two smooth tables as shown in the figure. A small moth (an insect) of mass 8m is sitting on end A of the rod and a spider (an insect) of mass 16m is sitting on the other end B. Both the insects start moving towards each other along the rod with the moth moving at speed 2v and the spider at half of this speed. They meet at a point P on the rod and the spider eats the moth. Also, let v=L/T, where T is a constant having value 4sec. The point P is at
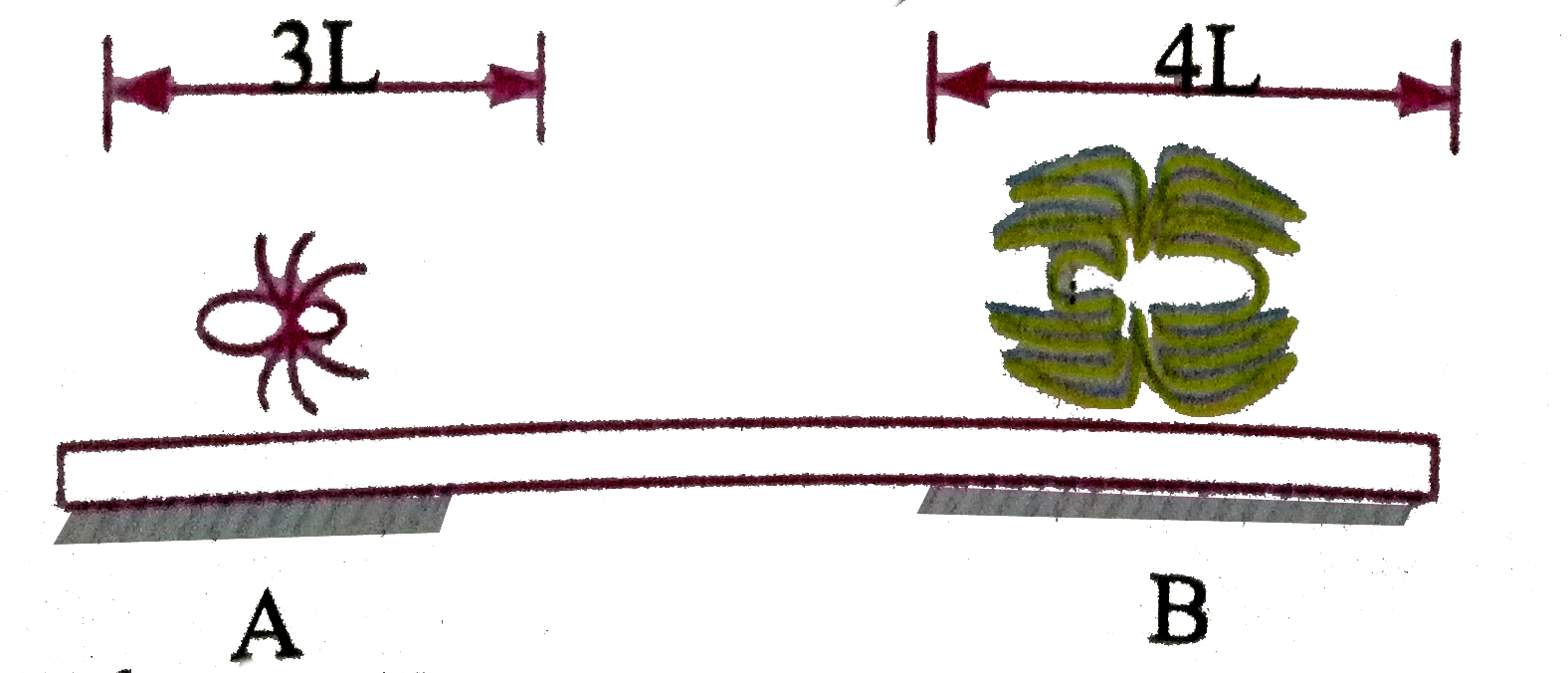
View SolutionAn air bubble is seen inside a solid sphere of glass (n=1.5) of 4.0cm diameter at a distance of 1.0cm from the surface of the sphere (on seeing along the diameter). Determine the real position of the bubble inside the sphere.
View Solution

