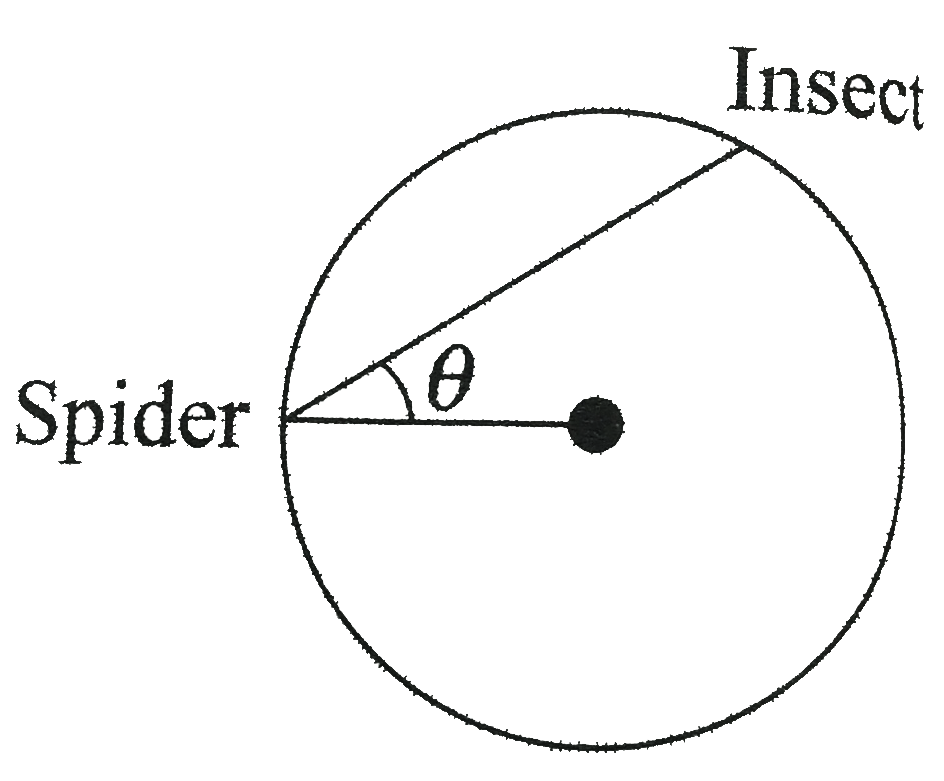
A spider and a fly are on the surface of a glass sphere. As the fly moves on the surface, find the maximum area on the glass sphere for the spider to be able to see it? Assume that the radius of the sphere (R) is much larger than the sizes of the spider and the fly. take the refractive index of glass μg to be equal to √2.
The correct Answer is:2πR2
Sin c =1μ⇒C=sin−1.1√2=45∘
_E01_155_S01.png)
Required area as shown in figure = 4πR22=2πR2
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-05 (A)35videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-05 (B)35videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-04[A]23videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II66videos
CURRENT ELECTRICITY
- BOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 49videos
GRAVITATION
Similar Questions
A mark on the surface of a glass spehre (μ=1.5) is viewed from a diametrically opposite position. It appears to be at a distance 10 cm from its actual position. The radius of the sphere is
View SolutionA spider is on the surface of a glass sphere with a refractive inndex of 1.5 . An insect crawls on the other side of the sphere as shown in Fig. For what maximum value of θ will the spider be able to still see the insect. Assume the spiders eye is in air.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A mark placed on the surface of a sphere is viewed through glass from a position directly opposite. If the diameter of the sphere is 10cm and refractive index of glass is 1.5, find the position of the image.
A−20cmB30cmC40cmD−10cm
A horizontal ray of light is incident on a solid glass sphere of radius R and refractive index μ . What is net deviation of the beam when it emerged from the other side of the sphere?
View SolutionA glass prothole is made at the botton of a ahip for observing sea life. The hole diameter D is much larger than the thickness of the glass. Determine the area S of the field of vision at the sea botton for the porthole of the refractive index of water is μw and the sea depth is h.
View SolutionAn object is at a distance of d=2.5cm from the surface of a glass sphere with a radius R=10cm. Find the position of the final image produced by the sphere. The refractive index of glass is μ=1.5.
View SolutionA parallel incident beam falls on a solid glass sphere at normal incidenc. Prove that the distance of the fianll image after two refractions is at a distance (2−μ)/2(μ−1)a from the outer edge of the sphere. Refractive index of the sphere is μ and radius of the sphere is a.
View SolutionA point object is placed at the center of a glass sphere of radius 6cm and refractive index 1.5. The distance of virtual image from the surface is
View Solution(i) The numberical value of the volume and surface of a sphere are equal. Find the diameter of the sphere.
(ii) The curved surved surface of a sphere is equal to the area of a circle of radius 2.8 cm. Find the volume of the sphere.View SolutionA small mass m starts from rest and slides down the surface of a frictionless solid sphere of radius R. Calculate the angle at which the mass flies off the sphere. If there is friction between the mass and the sphere, does the mass of fly off at a greater or lesser angle than the previous one ?
View Solution

