A spool of thread of mass m is placed on an inclined smooth plane set at an angleθ to the horizontal. The free end of the thread is attached to the wall as shown in figure-5.74. Calculate the acceleration of the centre of mass of the spool , if its moment of inertia about its axis is Iand the radius of the wound thread layer is r.
⎡⎢⎣g sinθ1+Imr2⎤⎥⎦
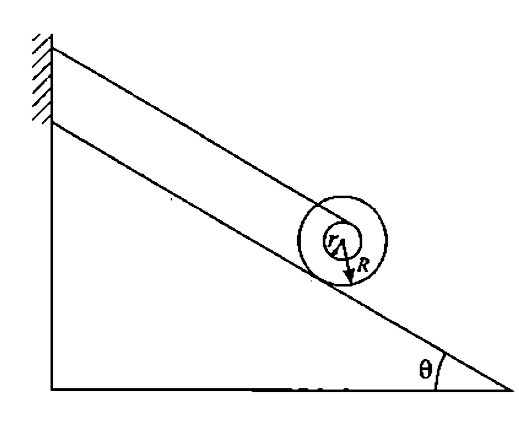
Step by step video & image solution for A spool of thread of mass m is placed on an inclined smooth plane set at an angletheta to the horizontal. The free end of the thread is attached to the wall as shown in figure-5.74. Calculate the acceleration of the centre of mass of the spool , if its moment of inertia about its axis is Iand the radius of the wound thread layer is r. [("g sin" theta)/(1 + (I)/(mr^(2)))] by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Discussion Question30videos
RIGID BODIES AND ROTATIONAL MOTION
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Conceptual MCQs Single Option Correct39videos
RIGID BODIES AND ROTATIONAL MOTION
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Unsolved Numerical63videos
RIGID BODIES AND ROTATIONAL MOTION
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Unsolved Numerical Problem81videos
NEWTONS LAWS OF MOTION
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - unsolved1videos
WORK, ENERGY AND POWER
Similar Questions
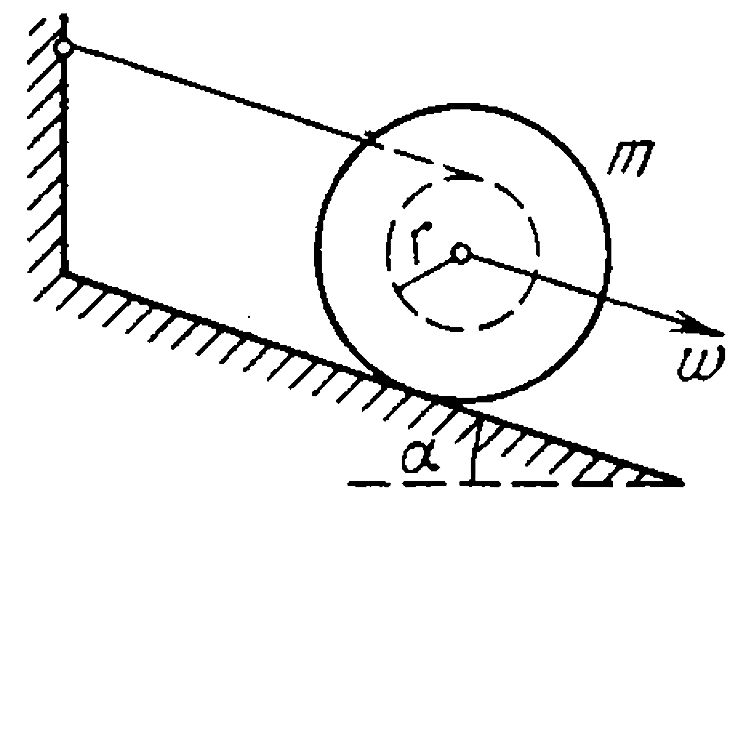
A spool with a thread wound on it is placed on an inclined smooth plane set an angle α=30∘ to the horizontal. The free end of the thread is attached to the wall as shown in figure. The mass of the spool is m=200g, its moment of inertia relative to its own axis I=0.45g⋅m2, the radius of the wound thread layer r=3.0cm. Find the acceleration of the spool axis.
 View Solution
View SolutionA uniform rod of mass m is kept in equilibrium making angle 30° with horizontal as shown, with a thread. The tension in the thread is?
View Solution
Knowledge Check
- Question 1 - Select One
A spool with a thread wound on it is placed on a smooth inclined plane set at an angle of 30 to the horizontal. The free end of the thread is attached to the wall as shown. The mass of the spool is m r m 200g, its moment of inertia relative to its own axis is I 0.45gm2, the radius of the wound thread layer is r 3 cm. The acceleration of the spool axis is:
 A0.5ms−2B5ms−2C1.4ms−2D14ms−2
A0.5ms−2B5ms−2C1.4ms−2D14ms−2 - Question 2 - Select One
The acceleration down the plane of spherical body of mass m radius R and moment of inertia I having inclination θ to the horizontal is
Agsinθ1+12/R2Bgsinθ1+I/R2Cgsinθ1+I/MR2DgsinθMR2+1 - Question 3 - Select One
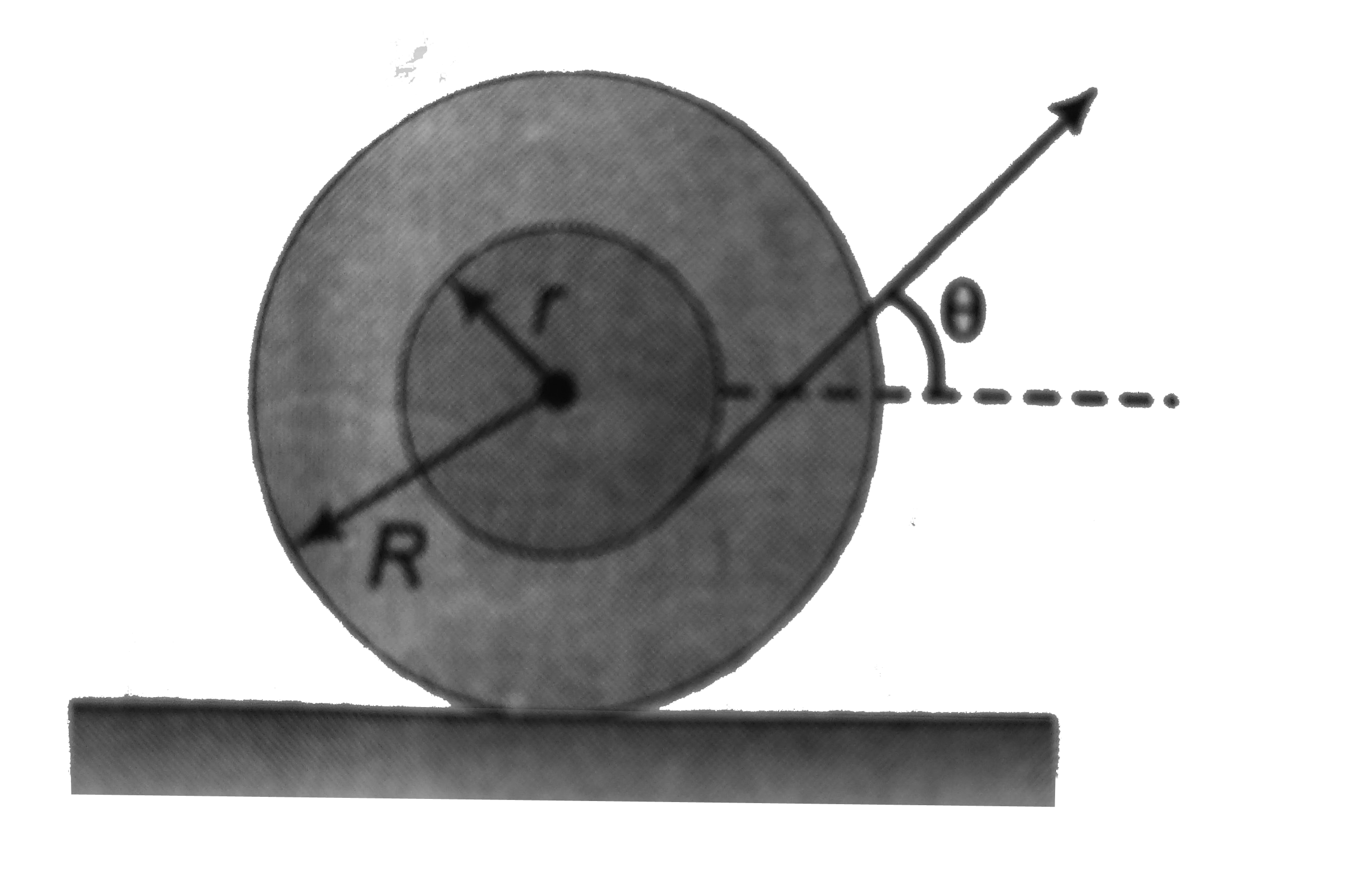
A spool is pulled at an angle θ with the horizontal on a rough horizontal surface as shown in the figure. If the spool remains at rest, the angle θ is equal toAcos−1(Rr)Bsin−1(√1−r2R2)Cπ−cos−1(rR)Dsin−1(rR)
A pulley fixed to the ceiling carried a thread with bodies of masses m1 and m2 attached to its ends. The mases of the pulley and the thread are negligible and friction is absent. Find the acceleration of the centre of mass of this system.
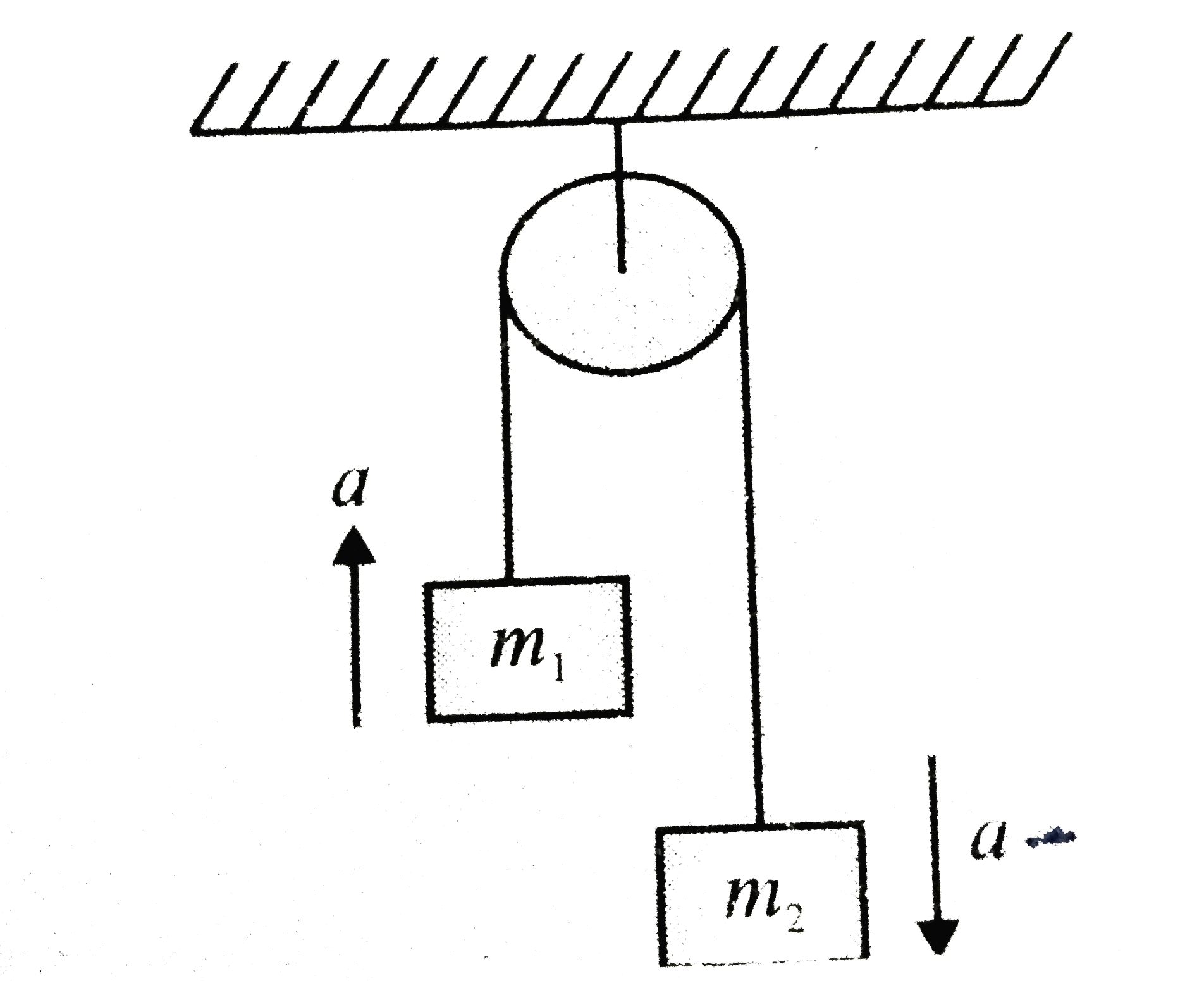 View Solution
View SolutionA block of mass M lies on a plane inclined at an angle α to the horizontal. A wieght a mass m is connected to the block by a thread slung over a pulley (Fig.).
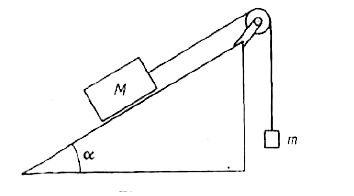
Find the acceleration of the weight and the tension of the thread. Friction, the mass of the pulley and of the thread are to be neglected.View SolutionFor the arrangement shown in the figure,blocks A and B are placed on the smooth horizontal surface.The free end P of the thread is being pulled by a constant force "F=1N" .Find the acceleration of free end P.
View SolutionA square of a side a is cut from a square of side 2a as shown in the figure. Mass of this square with a hole is M. Then its moment of inertia about an axis passing through its centre of mass and perpendicular to its plane will be
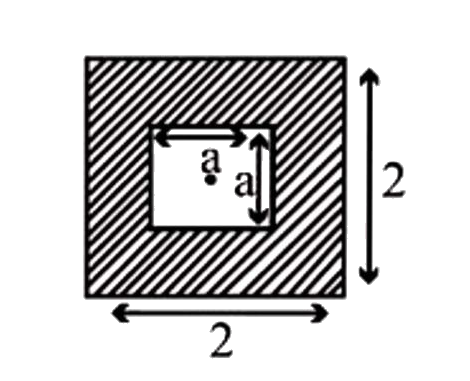 View Solution
View SolutionThread would around cylinder of mass M and radius R. It is allowed to fall as shown. Find its acceleration.
 View Solution
View Solution

