A spring block pendulum is shown in figure . The system is hanging in equilibrium. A bullet of mass m/2 moving at a speed u bites the block from downwards direction and gets embedded in it. Find the amplitude of oscillation of the block now. Also find the time taken by the block to reach its upper extreme position after hit by bullet.

If block is in equilibrium , then spring must be at some steretch if it is h, have mg=kh.
If a bullet of mass m/2 gets embedded in the block, due to this inelastic impact its new mass becoms 3m/2 and new mean positionof the block will be , say at a depth h1 from old mean position, then we must have
32mg=k(h+h1)
3m2g=k(h+h1)
h1=mg2k(asmg=kh)
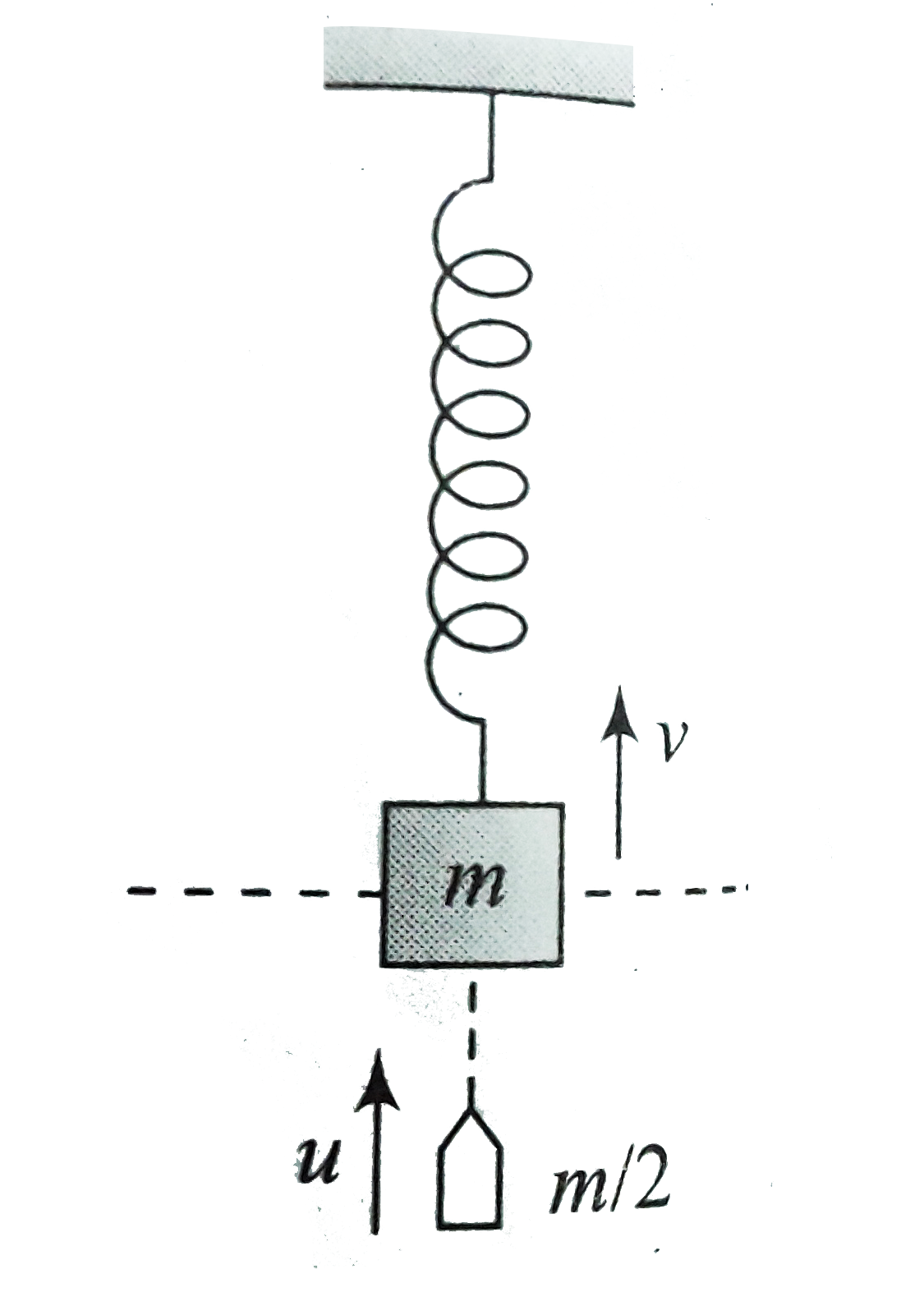
just after impact due to inelastic collition if the velocity of block becomes v, we have, according to momentum conservation.
m2μ=3m2νorν=u3
Now the block executes SHM and at t=0 block is at a distance h=mg2k above its mean position and having a velocity u/3. If amplitude of oscillation is A, we have
u3=ω√A2−(mg2k)2
or u29=2k3m[A2−(mg2k)2]
[as for this spring block system omega =√k(3m/2)]
A=√μ26k+(mg2k)2
Now time taken by partical to reach the topmost point can be obtained by circular motion representation as shown in figure. This figure shows the position of block P and its corresponding circular motion partical p0 at thet=0, Block P will reach its upper extereme position when partical P0 will traveres the angle θ and reach the topmost point as P0 moves at constant angular velocity ω, it will take a time given as
t=θω=cos−1(h1/A)√k3m/2=√3m2kcos−1(3mg2kA)

Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.1
23 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.2
23 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct Answer Type
9 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
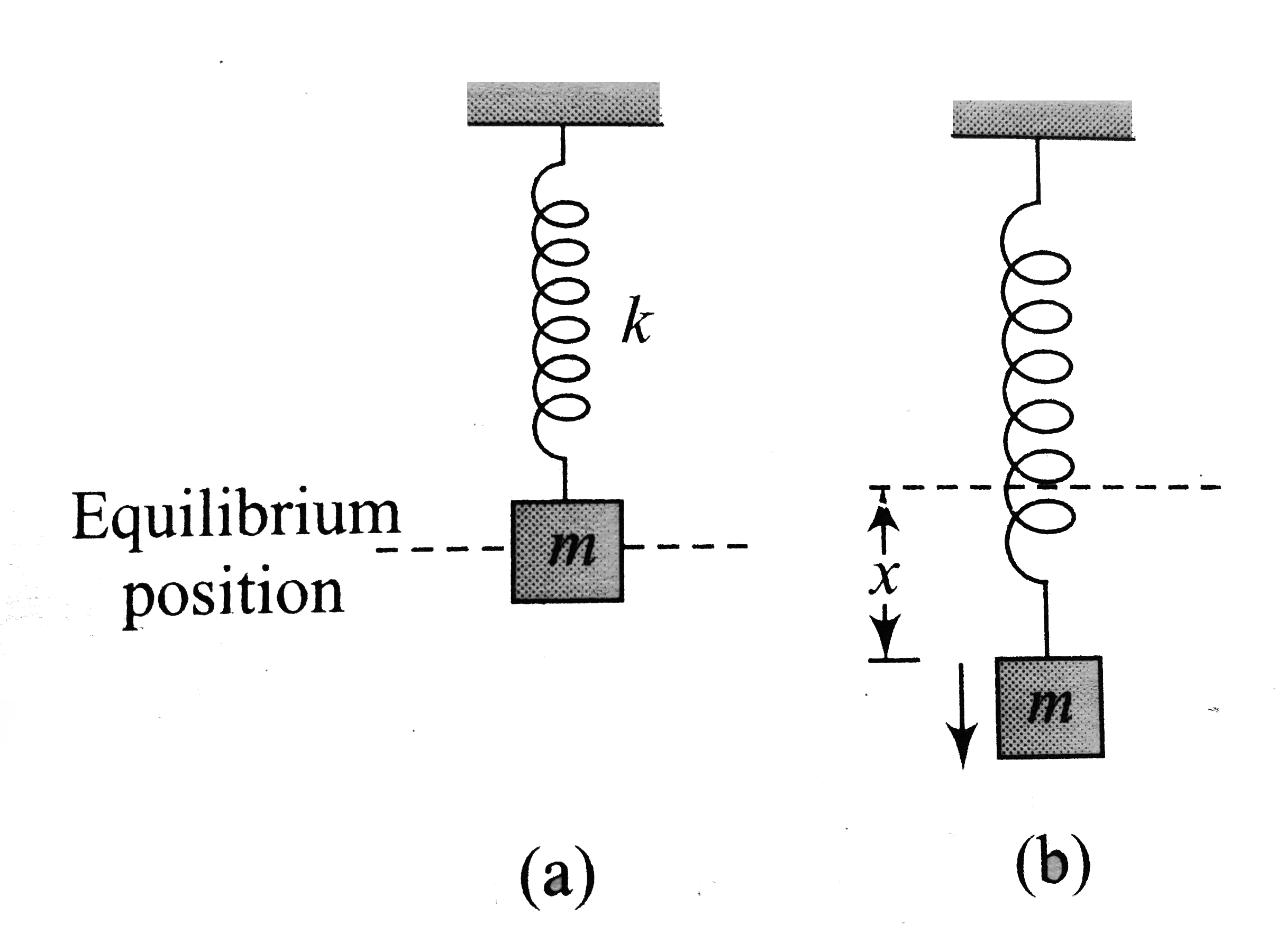
Figure shown a spring block system hanging in equilibrium. If a velocity v0 is imparted to the block in downwards direction . Find the amplitude of SHM of the block and the time after which it will reach a point at half the amplitude of block

View SolutionA bullet of mass m strikes a block of mass M. The bullet remains embedded in the block. Find the amplitude of the resulting SHM.

View Solution
Knowledge Check
A bullet of mass m moving with a speed v strikes a wooden block of mass M & gets embedded into the block. The final speed is
A√MM+nVB√mM+nVCmM+nVDV2A bullet of mass 'x' moves with a velocity y, hits a wooden block of mass z at rest and gets embedded in it. After collision, the wooden block and bullet moves with a velocity
Axx+zyBx+yxyCzx+yyDx+yzyA bullet of mass m travelling with a speed v hits a block of mass M initially at rest and gets embedded in it. The combined system is free to move and there is no other force acting on the system. The heat generated in the process will be
AzeroBmv22CMmv22(M−m)DmMv22(M+m)
Figure shown a spring block system hanging in equilibrium. The block of system is pulled down by the distance x and imparted a velocity v in downward direction as shown in figure. Find the time it will take to reach its mean position. Also find the maximum distance to which if will move before returning back towards mean position.
View SolutionA bullet of mass in travelling with a speed v hits a block of mass M initially at rest and gets embedded in it. The combined system is free to move and there is no other force acting on the system. The heat generated in the process will be
View SolutionA bullet of mass m moving horizontally with a velocity v strikes a block of wood of mass M and gets embedded in the block. The block is suspended from the ceiling by a massless string. The height to which block rises is
View SolutionIn the shown figure both blocks are in equilibrium m=1 kg. a bullet of mass m moves with velocity 10m/s and get embedded into the block A, then just after collision :
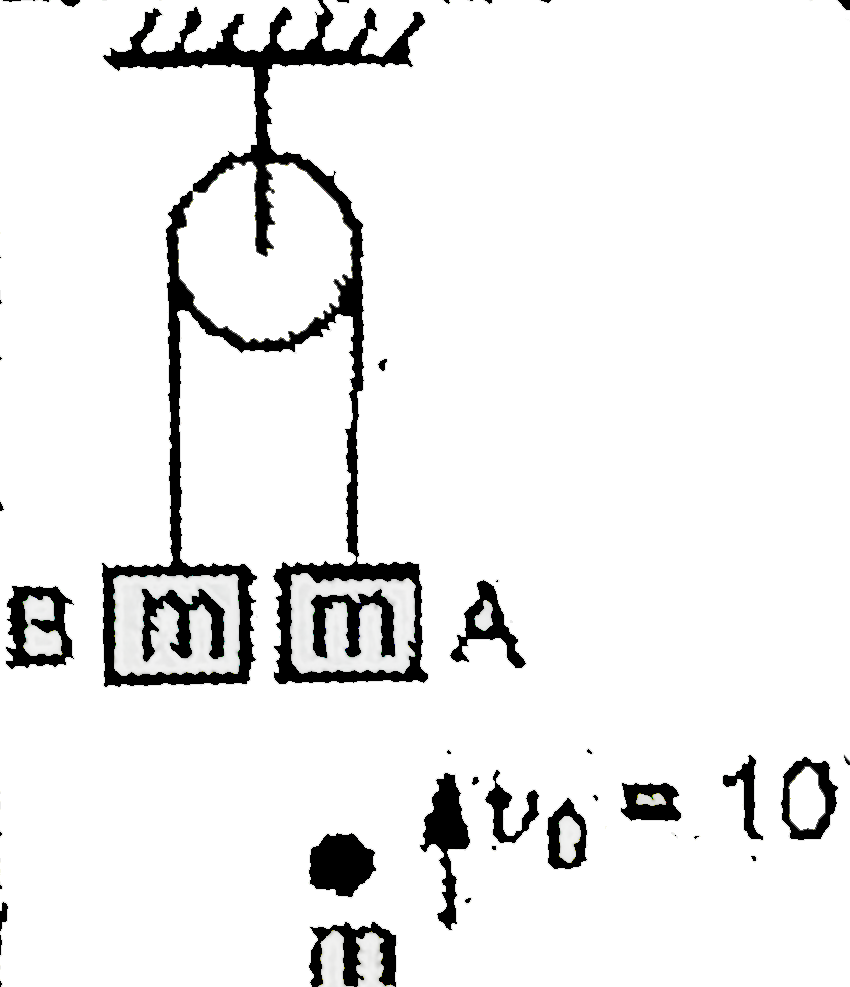
View SolutionThe length of ballistic pendulum is 1m and mass of its block is 0.98kg. A bullet of mass 20 gram strikes the block along horizontal direction and gets embedded in the block. If block + bullet completes vertical circle of radius 1m, then the striking velocity of bullet is
View Solution