A 2kg mass is attached to a spring of force constant 600N/m and rests on a smooth horizontal surface. A second mass of 1kg slides along the surface toward the first at 6m/s.
(a) Find the amplitude of oscillation if the masses make a perfectly inelastic collision and remain together on the spring. what is the period of oscillation ?
(b) Find the amplitude and period of oscillation if the collision is perfectly elastic.
( c) For each case , write down the position x as a function of time t for the mass attached to the spring, assuming that the collision occurs at time t=0. What is the impulse given to the 2kg mass in each case ?
a. From conservation of liner momentum.
1×6=(1+2)ν
∴Nu=2m/s
Now from conservation of mechanical energy.
12mv2=12kA2
A=(√mk)ν=(√3600)×2
or A=0.141m=14.1cm
T=2π√mk=2π√3600=0.44s

b. For perfectly elastic collision:
ν2'=(m2−m1m1+m2)ν2+(2m1m1+m2)ν1
or ν2'=(2×11+2)×6=4m/s
A=(√mkν2=(2600)1/2×4
or A=0.23m=23cm
T=2π√mk=2π√2600=0.36s
c. In the first case, ω=2πT=2π0.44=14.28rad/s
and amplitude A=14.1cm
x=Asinωt=(14.1cm)sin(14.28t)
In the second case, ω=2πT=2π0.36=17.45rad/s
and amplitude A=23cm
x=23sin(17.45t)cm
Impulase, J=ΔP=2×2=4N−s in the first case and 4×2=8N−s in the second case.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.123videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.223videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct Answer Type9videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger11videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type3videos
MISCELLANEOUS KINEMATICS
Similar Questions
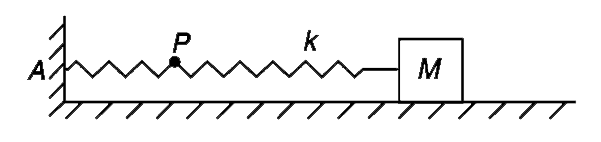
A block of mass M is tied to a spring of force constant k and placed on a smooth horizontal surface. The natural length of the spring is L. P is a point on the spring at a distance L4 from its fixed end. The block is set in oscillations with amplitude A. Find the maximum speed of point P on the spring.
 View Solution
View Solution
The period of oscillation of a mass M suspended from a spring of spring constant K is T. the time period of oscillation of combined blocks isView Solution
Knowledge Check
- Question 1 - Select One
A 1 kg mass is attached to a spring of force constant 600 N/m and rests on a smooth horizontal surface with other end of the spring tied to wall as shown in figure. A second mass of 0.5 kg slides along the surface towards the first at 3m/s. If the masses make a perfectly inelastic collision, then find amplitude and time period of oscillation of combined mass.
 A5cm,π10sB5cm,π5sC4cm,2π5sD4cm,π3s
A5cm,π10sB5cm,π5sC4cm,2π5sD4cm,π3s - Question 2 - Select One
The graph between period of oscillation (T) and mass attached (m) to a spring will be
A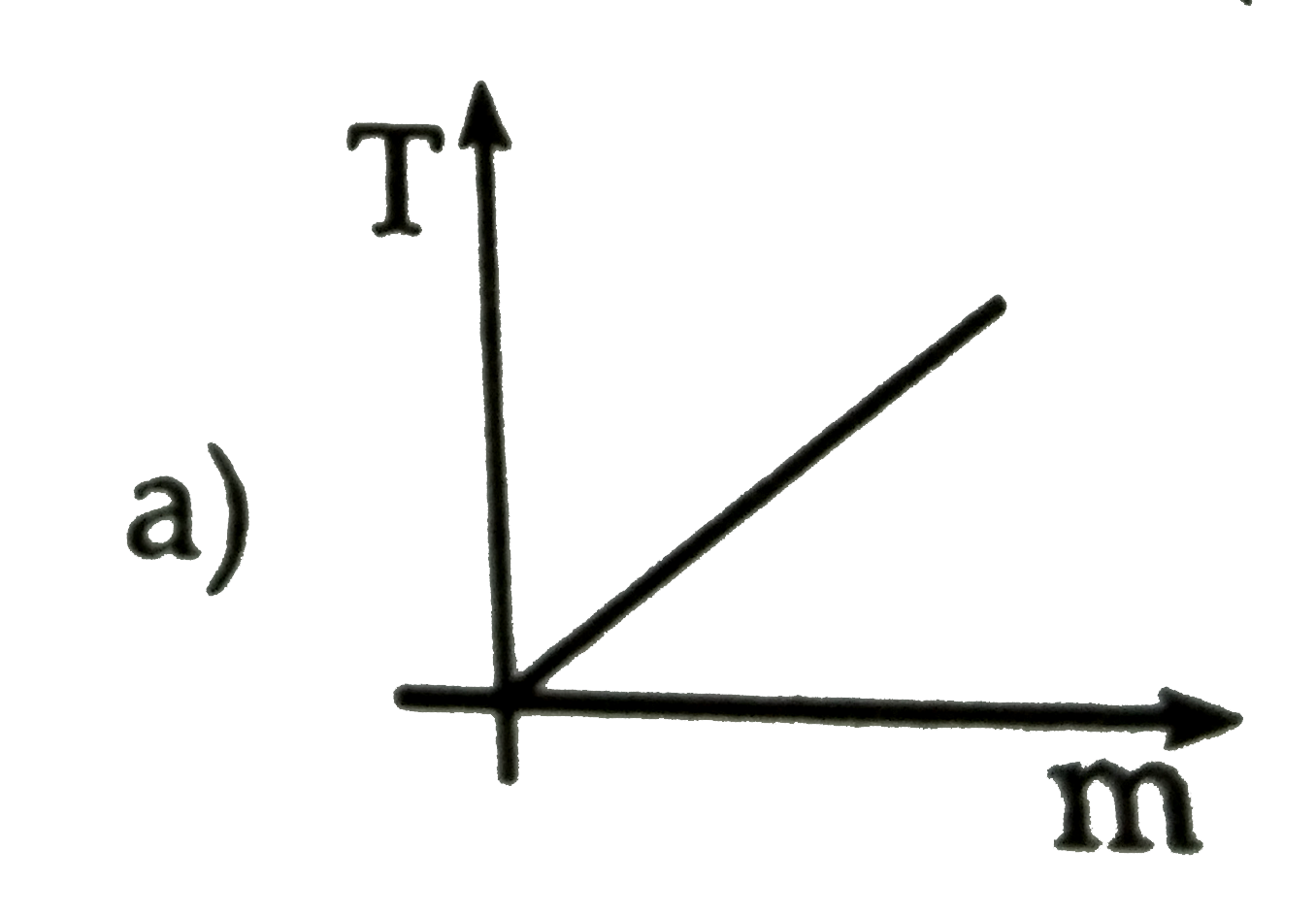 B
B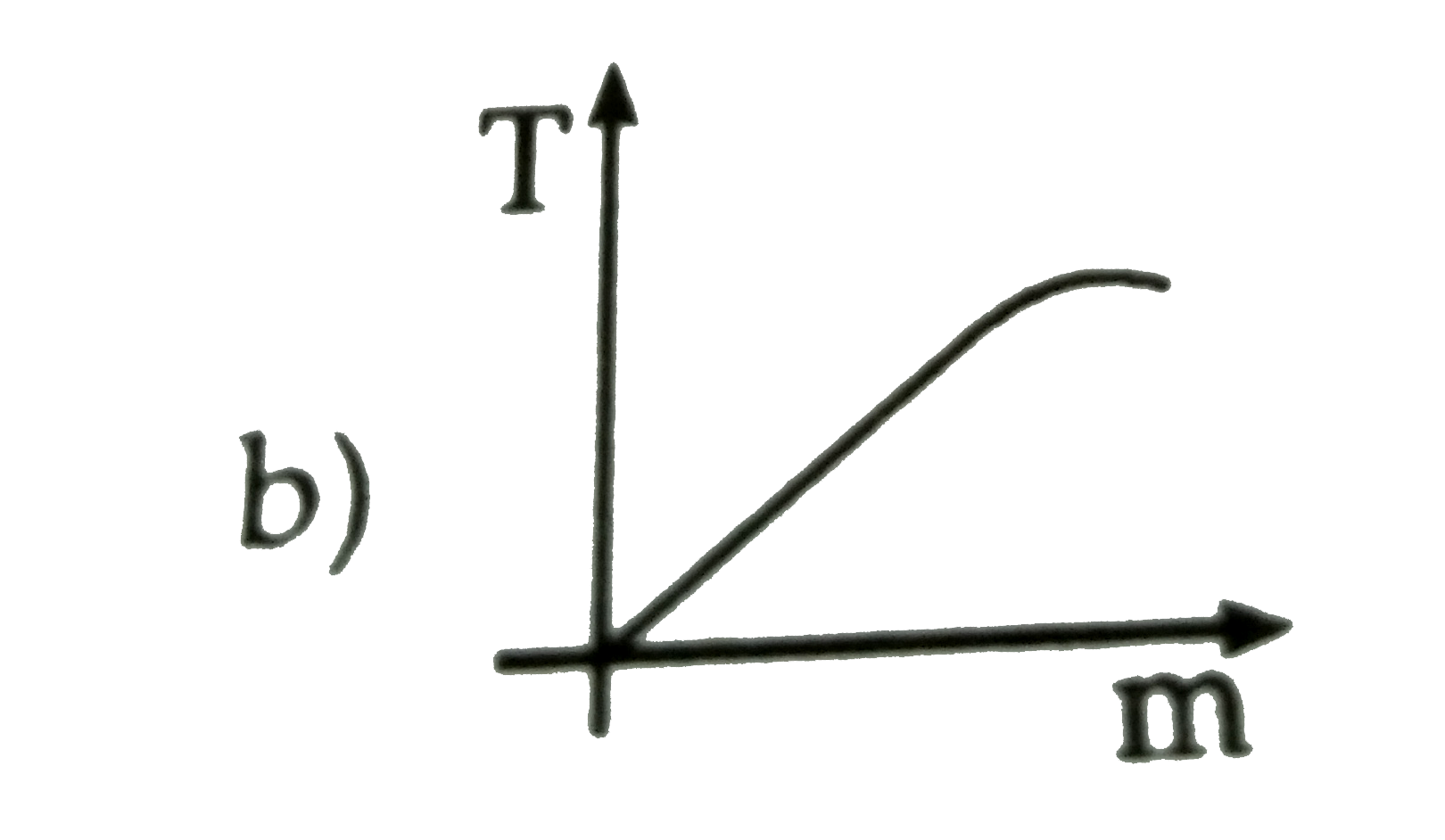 C
C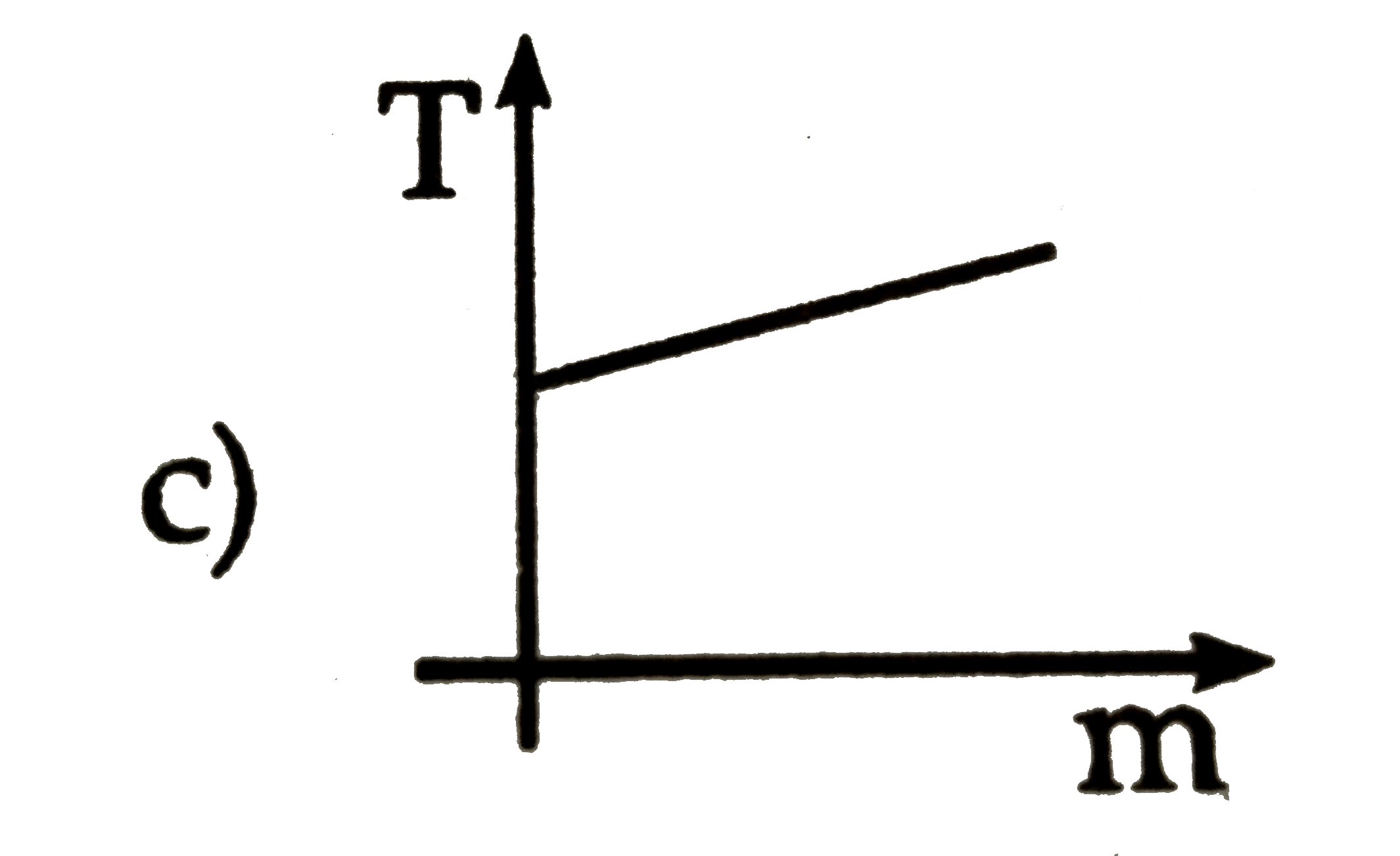 D
D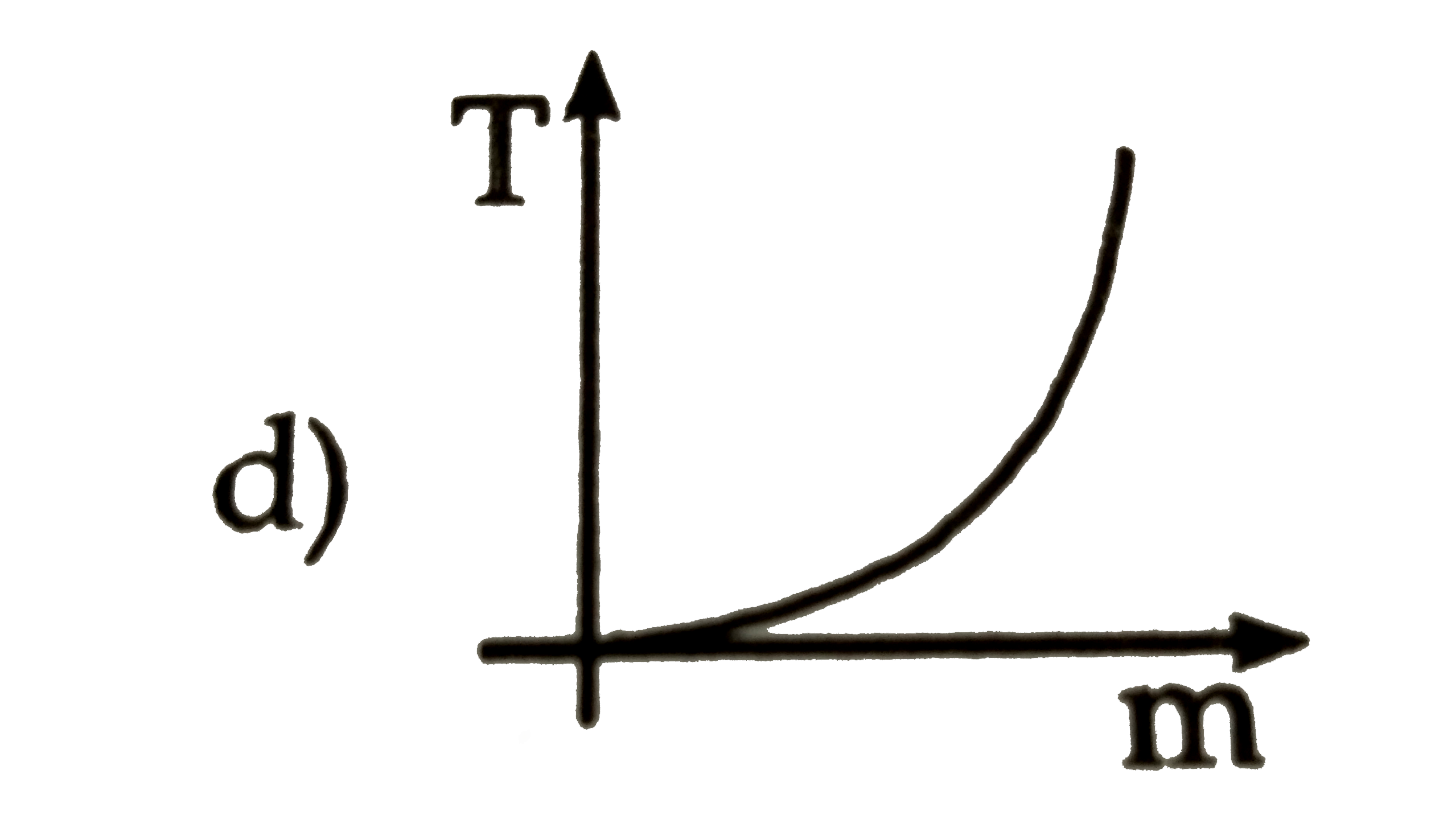
- Question 3 - Select One
a block of mass 0.1 kg attached to a spring of spring constant400Nm pulled horizontally from x=0 tox1=10mm. Find the work done by the spring force
A2⋅10−2JB2⋅10−6JC3⋅10−6JD4⋅10−2J
A block of mass 'm' is attached to the light spring of force constant K and released when it is in its natural length. Find amplitude of subsequent oscillations.
View SolutionA body of mass 1 kg oscillates on a spring of force constant 16 N/m. Calculate the angular frequency.
View SolutionA block of mass 0.2 kg is attached to a mass less spring of force constant 80 N/m as shown in figure. Find the period of oscillation. Take g=10m/s2. Neglect friction
 View Solution
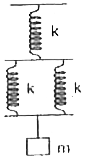
View SolutionCalculate the period of oscillations of block of mass m attached with a set of springs as shown
 View Solution
View SolutionA mass M is attached to a horizontal spring of force constant k fixed one side to a rigid support as shown in figure. The mass oscillates on a frictionless surface with time period T and amplitude A. When the mass M is in equilibrium position, another mass m is gently placed on it. When will be the new amplitude of ocillation?
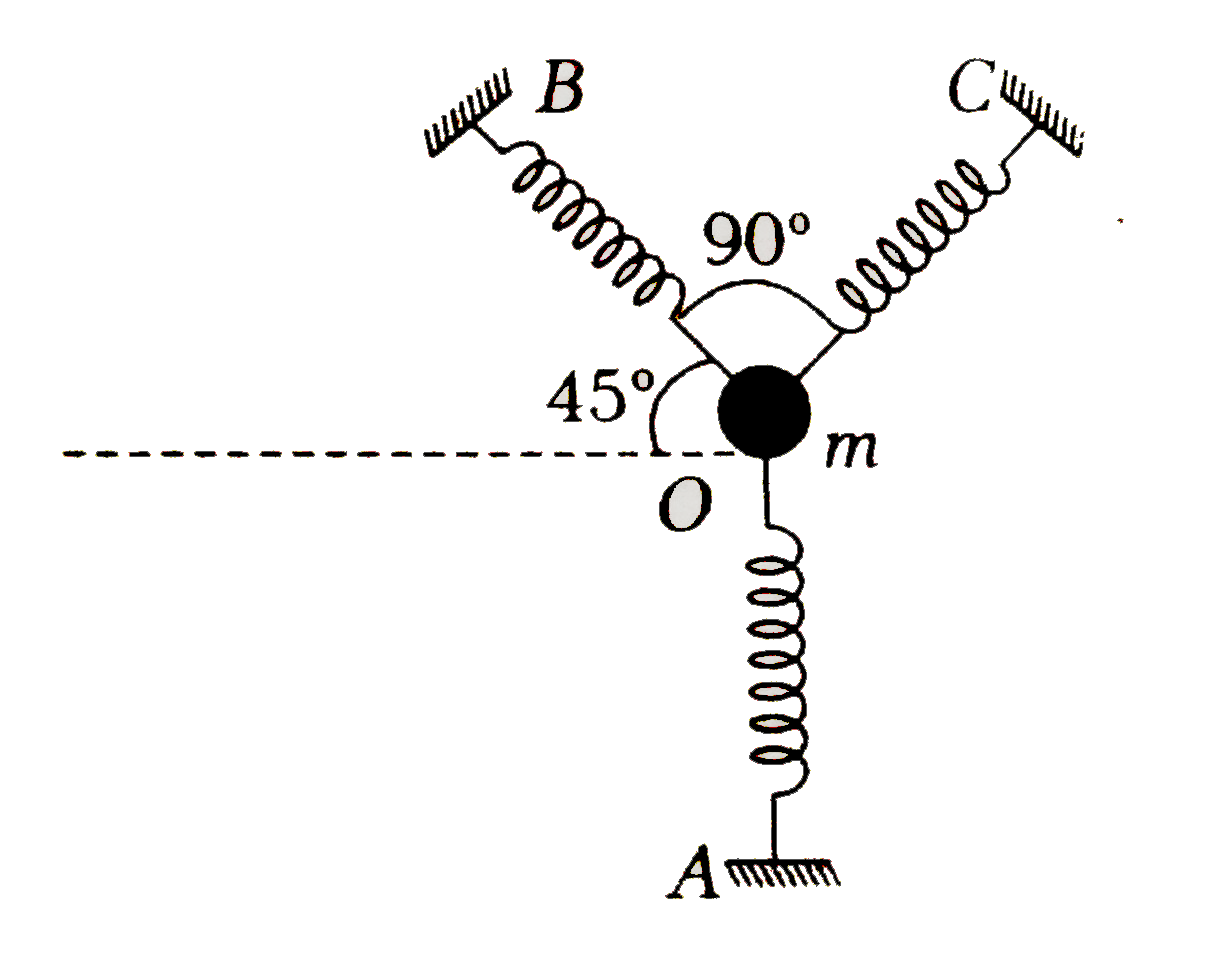
 View Solution
View Solution

