A spring having a spring constant 1200Mn−1 is mounted on a horizontal table. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 0.02 m and released. Determine (i) frequency of oscillations (ii) maximum acceleration of the mass and (iii) the maximum speed of the mass. Solution in Kannada
Given, k=1200Nm−1,m=3kg,y=0.02m
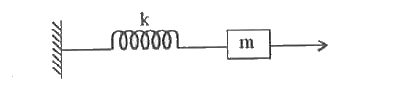
(i) Frequency of oscillation, f=12π√km
i.e. f=(12×3.142)√12003=103.142=(10π)Hz
(ii) maximum acceleration of the mass,
amax=−ω2y where ω=2πT=2πf
i.e. ω=2π×10π
hence amax=−20×20×0.02
amax=8ms−2
(iii) maximum speed of the mass,
vmax=ωA=2×0.02=0.4ms−1.
Topper's Solved these Questions
- OSCILLATIONSBOOK - SUBHASH PUBLICATIONCHAPTER - OSCILLATIONSEXERCISE - FIVE MARKS QUESTIONS WITH ANSWERS
4 Videos
- MOTION IN PLANEBOOK - SUBHASH PUBLICATIONCHAPTER - MOTION IN PLANEEXERCISE - NUMERICALS WITH SOLUTIONS
47 Videos
- PHYSICAL WORLDBOOK - SUBHASH PUBLICATIONCHAPTER - PHYSICAL WORLDEXERCISE - TWO MARKS QUESTIONS WITH ANSWERS
30 Videos
Similar Questions
Arrive an expression for time period of simple pendulum.
View SolutionTwo forces 8N and 5N are acting at a point on a body at an angle 120∘ then find the (i) magnitude and (ii) direction of their resultant.
View SolutionMathematics is the language of physics. Justify the statement.
View SolutionA spring of force constant 1200Nm−1 is mounted on a horizontal table as shown in figure. A mass of 3.0kg is attached to the free end of the spring, pulled side ways to a distance of 2.0cm and released. Determing.
(a) the frequency of oscillation of the mass.
(b) the maximum acceleration of the mass.
(c) the maximum speed of the mass.

View SolutionA spring of force constant 600Nm−1 is mounted on a horizontal table. A mass of 1.5 kg is attached to the free end of the spring,pulled sideways to a distance of 2 cm and released . The speed of the mass when the spring is compressed by 1 cm is
View SolutionA spring having with a spring constant 1200 N m^(-1) is mounted on a horizontal table as shown in Fig. 14.24. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released. Determine (i) the frequency of oscillations, (ii) maximum acceleration of the mass, and (iii) the maximum speed of the mass.
View SolutionA spring having with a spring constant 1200 N m^(-1) is mounted on a horizontal table as shown in Fig. 14.24. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released. Determine (i) the frequency of oscillations, (ii) maximum acceleration of the mass, and (iii) the maximum speed of the mass.
View SolutionA spring of force constant 1200Nm−1 is mounted on a horizontal table as shown in figure. A mass of 3.0kg is attached to the free end of the spring, pulled side ways to a distance of 2.0cm and released. Determing.
(a) the frequency of oscillation of the mass.
(b) the maximum acceleration of the mass.
(c) the maximum speed of the mass.

View SolutionA spring having with a spring constant 1200Nm−1 is mounted on a horizontal table as shown in Fig. 14.24. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released.
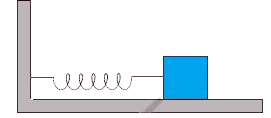
Determine (i) the frequency of oscillations, (ii) maximum acceleration of the mass, and (iii) the maximum speed of the mass.
View SolutionA spring having with a spring constant 1200Nm−1 is mounted on a horizontal table as shown in Fig. 14.24. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released.

Determine (i) the frequency of oscillations, (ii) maximum acceleration of the mass, and (iii) the maximum speed of the mass.
View SolutionA spring having with a spring constant 1200Nm−1 is mounted on a horizontal table as shown in Fig. 14.24. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released.

Determine (i) the frequency of oscillations, (ii) maximum acceleration of the mass, and (iii) the maximum speed of the mass.
View SolutionA spring having with a spring constant 1200Nm−1 is mounted on a horizontal table as shown in Fig. 14.24. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released.
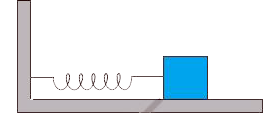
Determine (i) the frequency of oscillations, (ii) maximum acceleration of the mass, and (iii) the maximum speed of the mass.
View SolutionA spring having with a spring constant 1200Nm−1 is mounted on a horizontal table as shown in Fig. 14.24. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released.
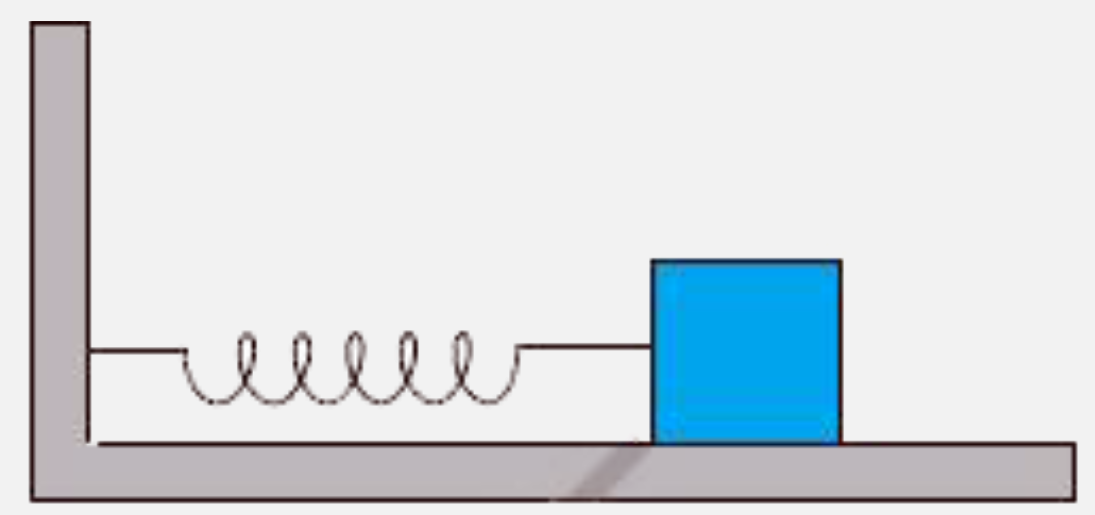
Determine (i) the frequency of oscillations, (ii) maximum acceleration of the mass, and (iii) the maximum speed of the mass.
View SolutionA spring having spring constant 1200Nm−1 is mounted on a horizontal table as shown in figure. A mass of 3kg is attached to the free end of the spring. The mass is the pulled sideways to a distance of 2.0cm and released. Determine the frequency of oscillations.
View SolutionA spring having spring constant 1200Nm−1 is mounted on a horizontal table as shown in figure. A mass of3kg is attached to the free end of the spring. The mass is the pulled sideways to a distance of 2.0cm and released. Determine maximum acceleration of the mass.
View Solution
