A spring having with a spring constant is mounted on a horizontal table as shown in Fig. 14.24. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released.
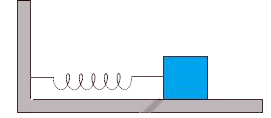
Determine (i) the frequency of oscillations, (ii) maximum acceleration of the mass, and (iii) the maximum speed of the mass.Solution in Bengali
Frequency , maximum acceleration of the mass 8.0 m , maximum speed of the mass 0.4 m .
Topper's Solved these Questions
- BOOK - NCERT BANGLISHCHAPTER - OSCILLATIONSEXERCISE - Additional Exercises6videos
OSCILLATIONS
- BOOK - NCERT BANGLISHCHAPTER - OSCILLATIONSEXERCISE - Additional Exercises6videos
OSCILLATIONS
- BOOK - NCERT BANGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ADDITIONAL EXERCISES5videos
MOTION IN A STRAIGHT LINE
- BOOK - NCERT BANGLISHCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EXERCISES (TRUE OR FALSE)3videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
Similar Questions
An air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.14.27). Show that when the ball is pressed down a little and released , it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.27].
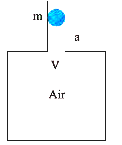 05:14View Solution
05:14View SolutionAn air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.14.27). Show that when the ball is pressed down a little and released , it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.27].
 03:02View Solution
03:02View SolutionA boy standing on a stationary lift (open from above) throws a ball upwards with the maximum initial speed he can, equal to 49ms−1. How much time does the ball take to return to his hands ? If the lift starts moving up with a uniform speed of 5ms−1 and the boy again throws the ball up with the maximum speed he can, how long does the ball take to return to his hands ?
03:02View SolutionThe instantaneous speed of the point of contact during rolling is zero.
03:02View SolutionA spring having a spring constant 1200Mn^(-1) is mounted on a horizontal table. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 0.02 m and released. Determine (i) frequency of oscillations (ii) maximum acceleration of the mass and (iii) the maximum speed of the mass.
03:02View SolutionA spring having with a spring constant 1200 N m^(-1) is mounted on a horizontal table as shown in Fig. 14.24. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released. Determine (i) the frequency of oscillations, (ii) maximum acceleration of the mass, and (iii) the maximum speed of the mass.
View SolutionA spring having with a spring constant 1200Nm−1 is mounted on a horizontal table as shown in Fig. 14.24. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released.

Determine (i) the frequency of oscillations, (ii) maximum acceleration of the mass, and (iii) the maximum speed of the mass.03:36View SolutionA spring having with a spring constant 1200Nm−1 is mounted on a horizontal table as shown in Fig. 14.24. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released.

Determine (i) the frequency of oscillations, (ii) maximum acceleration of the mass, and (iii) the maximum speed of the mass.View SolutionA spring having with a spring constant 1200Nm−1 is mounted on a horizontal table as shown in Fig. 14.24. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released.

Determine (i) the frequency of oscillations, (ii) maximum acceleration of the mass, and (iii) the maximum speed of the mass.View SolutionA spring having with a spring constant 1200Nm−1 is mounted on a horizontal table as shown in Fig. 14.24. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released.
Determine (i) the frequency of oscillations, (ii) maximum acceleration of the mass, and (iii) the maximum speed of the mass.View SolutionA spring having with a spring constant 1200Nm−1 is mounted on a horizontal table as shown in Fig. 14.24. A mass of 3 kg is attached to the free end of the spring. The mass is then pulled sideways to a distance of 2.0 cm and released.
Determine (i) the frequency of oscillations, (ii) maximum acceleration of the mass, and (iii) the maximum speed of the mass.View SolutionA spring of force constant 1200 Nm−1 is mounted on a horizontal table as shown in Fig.

A mass of 3.0 kg is attached to the free end of the spring, pulled side ways to a distance 2.0 cm and released. Determine the maximum acceleration of the mass.02:48View SolutionA spring of force constant 1200 Nm−1 is mounted on a horizontal table as shown in Fig.

A mass of 3.0 kg is attached to the free end of the spring, pulled side ways to a distance 2.0 cm and released. Determine the maximum speed of the mass.03:42View SolutionA spring of force constant 1200Mm−1 Is mounted on a horizontal table as shown in Fig. A mass of 3.0 kg is attached to the free end of the spring, pulled side ways to a distance 2.0 cm and released. Determine

the maximum acceleration of the mass.03:08View SolutionA spring of force constant 1200Mm−1 Is mounted on a horizontal table as shown in Fig. A mass of 3.0 kg is attached to the free end of the spring, pulled side ways to a distance 2.0 cm and released. Determine

the maximum speed of the mass.02:02View Solution

